1.3.Кинематика вращательного движения абсолютно твёрдого тела

При вращательном движении твердого тела все его точки движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения (рис.1.5). При этом радиус-векторы, проведенные из центров соответствующих окружностей к точкам тела за равные промежутки времени, поворачиваются на один и тот же угол. Угол поворота  любого из радиуc-векторов определяет угловой путь, пройден- ный телом за данный промежуток времени t. Очень малые углы поворота можно рассматривать как векторы , совпадающие с осью, направление которых связано с направлением вращения тела правилом правого винта. Такие векторы называются аксиальными.

Быстроту изменения углового перемещения с течением времени определяет угловая скорость

= . (1.24)

Угловая скорость является аксиальным вектором, который направлен вдоль оси вращения в соответствии с правилом правого винта.

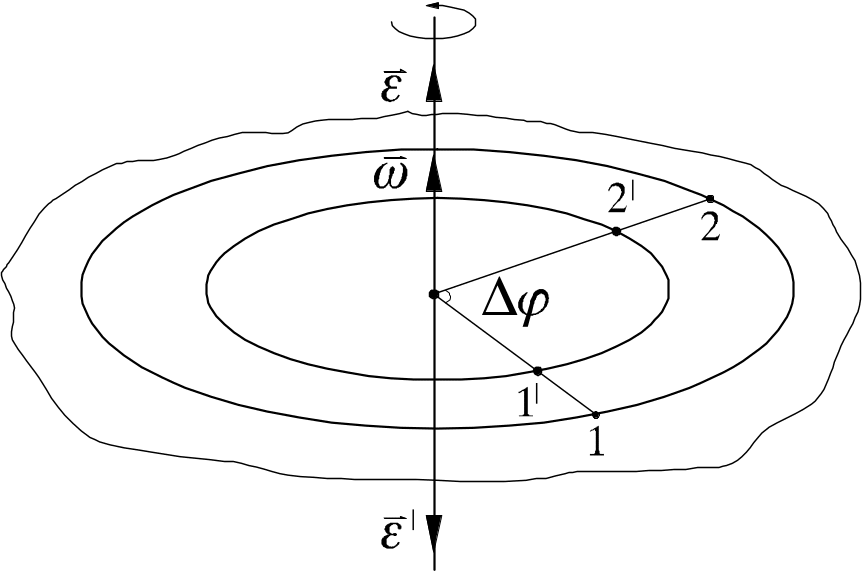
Рис.1.5

Быстроту изменения угловой скорости характеризует вектор углового ускорения

= = . (1.25)

Направление вектора либо совпадает с направлением угловой скорости (при ускоренном вращении >0) либо противоположно ему (при замедленном вращении <0).

Угловой путь, угловая скорость и угловое ускорение при равноускоренном вращении связаны между собой формулами, аналогичными формулам равноускоренного прямолинейного движения

, (1.26)

, (1.27)

где ₀ – начальная угловая скорость.

Кроме угловых характеристик, движение каждой точки вращающегося тела характеризуют линейные величины , a, a_n, a_ (рис.1.6).

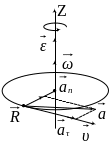
Рис.1.6

Между угловыми и линейными характеристиками движения существуют следующие соотношения:

,  =  R . (1.28)

a_ =  R , a_n =  ² R = , (1.29)

1.4. Динамика вращательного движения

Основными динамическими характеристиками абсолютно твердого тела при вращательном движении являются момент инерции и момент импульса.

1.4.1. Момент инерции и момент импульса

Моментом инерции тела относительно оси z является сумма произведений элементарных масс на квадраты расстояний от них до данной оси:

,. (1.30)

где и - масса i-й точки и ее расстояние от оси.

Момент инерции есть мера инертности твердого тела к изменению его угловой скорости. Чем больше момент инерции, тем труднее изменить его угловую скорость. Следовательно, момент инерции тела при вращательном движении играет такую же роль, что и масса при поступательном движении.

Момент инерции тела является величиной аддитивной. Вычисление момента инерции тела производится по формулам

, (1.31)

где dm и dV – масса и объем элемента тела, находящегося на расстоянии r от оси z,  – плотность тела в данной точке.

Моменты инерции некоторых однородных тел правильной геометрической формы относительно оси z, проходящей через центр массы тела, приведены в табл. 1.2.

Твердое тело	Ось	Момент инерции
Кольцо радиусом R	Совпадает с осью кольца	I = m R2
Сплошной цилиндр радиусом R	Совпадает с осью цилиндра	I = m R2
Шар радиусом R	Проходит через центр шара	I = m R2
Тонкий стержень длиной l	Перпендикулярна стержню, проходит через его центр	I = m l2

Таблица 1.2

Момент инерции I_x тела относительно произвольной оси равен сумме момента инерции тела I_c относительно параллельной ей оси, проходящей через центр масс С, и произведения массы тела m на квадрат расстояния d между этими осями (теорема Штейнера):

I_x = I_c + md². (1.32)

Момент импульса является основной количественной мерой вращательного движения тела. Различают момент импульса тела относительно неподвижной точки (полюса) и относительно неподвижной оси.

Моментом импульса материальной точки относительно точки О называется векторное произведение радиус-вектора , проведенного из полюса О в место нахождения материальной точки, на импульс этой точки (рис. 1.7):

, (1.33)

где m и – масса и скорость материальной точки.

Вектор перпендикулярен плоскости в которой расположены векторы от и , а его направление определяется правилом правого винта: при вращении рукоятки буравчика от к , его поступательное движение совпадает с направлением (рис. 1.7)

Рис.1.7

Модуль момента импульса равен:

L = r p sin,

где  - угол между и .

М оментом импульса системы относительно неподвижной точки О называется геометрическая сумма моментов импульса относительно той же точки О всех материальных точек системы

, (1.34)

где от к , - радиус-вектор и импульс i-й материальной точки, а n – общее число этих точек в системе.

Моментом импульса системы относительно неподвиж -ной оси z называется величина L_z, равная проекции на эту ось вектора L момента импульса системы относительно какой либо точки О, принадлежащей этой оси:

_z . (1.35)

Выбор положения точки О на оси z не влияет на численное значение L_z. В частности, если твердое тело вращается вокруг неподвижной оси z с угловой скоростью , то его момент импульса относительно этой оси:

L_z = I_z  _z. . (1.36)

Здесь I_z – момент инерции тела относительно оси z, а _z - проекция вектора на ось z. Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость.