Решение

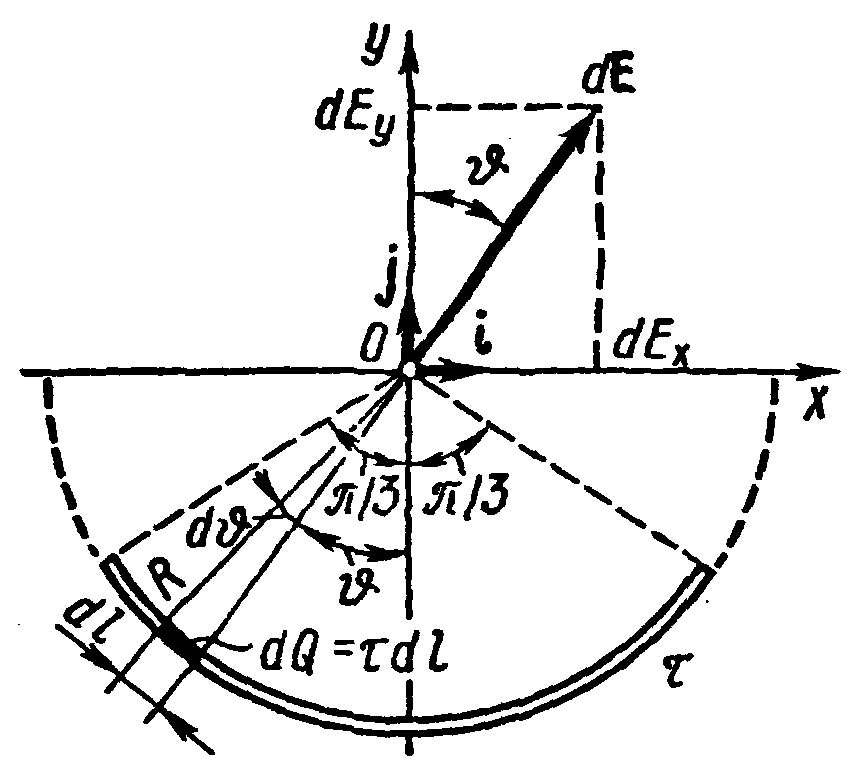Выберем оси координат так, чтобы начало координат совпало с центром кривизны дуги, а ось Oy была бы симметрично расположена относительно концов дуги. На нити выделим элемент длины dl. Заряд dQ=dl, находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность dE поля, создаваемого зарядом dQ:

г де – радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность.

Выразим вектор dE через проекции dE_x и dE_y на оси координат:

,

где и – единичные векторы направлений (орты).

Напряженность Е найдем интегрированием. Интегрирова- ние ведется вдоль дуги длиной l.

В силу симметрии . Тогда

, (1)

г де

Т ак как r=R=const, , то

Подставим в выражение (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до /3, а результат удвоим:

В ыразив радиус R через длину l нити (3l=2R), получим

(2)

Из этой формулы видно, что напряженность поля по направлению совпадает с осью Оу.

Найдем потенциал электрического поля в точке О. Сначала найдем потенциал d, поля создаваемого точечным зарядом dQ в точке О:

d = dl /(4₀ r).

З аменим r на R и проведем интегрирование:

Так как l = 2R/3, то

 = /(6₀). (3)

Произведем вычисления по формулам (2) и (3):

Задача 3. На тонком стержне длиной l равномерно распределен заряд с линейной плотностью  =10 нКл/м. Найти потенциал , созданный распределенным зарядом в точке А, расположенной на оси стержня и удаленной от его ближайшего конца на расстояние l.

Решение

В задаче рассматривается поле, создаваемое распределен- ным зарядом. В этом случае поступают следующим образом. На стержне выделяют малый участок длиной dx. Тогда на этом участке будет сосредоточен заряд dQ =  dx, который можно считать точечным.

Потенциал d, создавае- мый этим точечным зарядом в точке А, можно определить по формуле

С огласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным стержнем в точке А, найдем интегрированием этого выражения:

П одставим числовые значения физических величин в СИ (=10·10^-9 Кл/м, 1/(4₀)=9·10⁹ м/Ф) и произведем вычисления:

 = 9_·10⁹_·10_·10^-9_·0,693 = 62,4 В.

Задача 4. Какую работу надо совершить, чтобы перенести точечный заряд Кл из бесконечности в точку, находящуюся на расстоянии l=10 см от поверхности метали- ческого шарика? Потенциал шарика В, радиус его R=2 см. Шарик находится в воздухе.

Решение

Искомая работа с учетом того, что потенциал в бесконечности равен нулю, определяется по формуле:

,

где  – потенциал поля в данной точке.

Этот потенциал найдем по формуле для поля точечного заряда как если бы заряд Q, находящийся на поверхности шара, был расположен в центре шара

.

Потенциал на поверхности шарика связан с электроемкостью шара ( ) формулой

.

Отсюда, . Таким образом, .

Следовательно, искомая работа мкДж.

Задача 5. Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью . Напряженность поля в конденсаторе , длина конденсатора l = 5см. найти модуль и направление скорости электрона в момент вылета из конденсатора. На сколько отклонится электрон от первоначального направления?