3. Электростатика

Электростатика изучает свойства и взаимодействие обладающих электрическим зарядом тел и частиц.

3.1. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона

В природе существуют два типа электрических зарядов: положительные и отрицательные. Электрический заряд любого тела дискретен, т.е. кратен элементарному электрическому заряду е ( ). Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.

Электронейтральность тел и систем объясняется рав- ным количеством положительно и отрицательно заряженных частиц в них. Отрицательный заряд у тел объясняется избы-точным количеством электронов в них по сравнению с числом протонов, а положительный – их недостатком.

Распределение макроскопического заряда в простран- стве характеризуется введением понятия объемной r, поверх- ностной d и линейной l плотности:

; ; , (3.1)

где dq – заряд, заключённый соответственно в объёме dV, на поверхности dS и длине dl.

В случае неоднородного распределения заряда, вели- чина q находится путём интегрирования соответствующей плотности:

; ; . (3.2)

Все изменения в макро- и микромире происходят с соблюдением закона сохранения электрического заряда, согласно которому в изолированной системе алгебраическая сумма зарядов всех частиц остается неизменной

. (3.3)

Наличие у тела электрического заряда проявляется во взаимо- действии его с другими заряженными телами. Разноименные заряды притягиваются, одноименные – отталкиваются. Основным законом электростатики является закон Кулона, который определяет силу взаимодействия точечных зарядов. Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

Закон Кулона: сила взаимодействия двух неподвиж-

ных точечных зарядов в вакууме (воздухе) прямо пропорцио- нальна произведению модулей зарядов и и обратно пропорциональна квадрату расстояния r между ними

, (3.4)

где k – коэффициент пропорциональности, величина которого зависит от выбора системы единиц;

, здесь – электрическая постоянная.

В векторной форме закон Кулона имеет вид

, (3.5)

где r – вектор, проведенный от одного заряда к другому и

имеющий направление к тому из зарядов, к которому приложена сила (рис.3.1).

Силы кулоновского взаимодействия являются централь- ными, т.е. направлены вдоль прямой, соединяющей заряды.

2. Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции полей

Взаимодействие зарядов осуществляется посредством электрического поля – одного из видов материи. Оно существует вокруг заряженных тел и действует на заряды, помещенные в поле, с некоторой силой. Поле, создаваемое неподвижными зарядами и не изменяющееся со временем, называется электростатическим.

Силовой характеристикой электрического поля является напряженность – это векторная физическая величина, численно равная силе, с которой поле действует на единичный положительный пробный заряд , помещен- ный в данную точку поля, и направленная в сторону действия силы ( ):

. (3.6)

Словами “пробный заряд” подчеркивается то обстоятельство, что он не участвует в создании исследуемого поля и не искажает его, т.е. что он достаточно мал и не вызывает перераспределения зарядов, с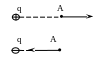 оздающих поле.

Рис. 3.1 Рис. 3.2

Если поле создано положительным зарядом, то вектор направлен вдоль радиуса-вектора от заряда; если поле создано отрицательным зарядом, то вектор направлен к заряду (рис. 3.2).

Для поля точечного заряда q сила , действующая на пробный заряд со стороны поля, будет равна

Тогда в соответствии с формулой (3.6) напряженность поля точечного заряда

, (3.7)

а модуль этого вектора будет равен

, (3.8)

где r – расстояние до заряда, создающего поле.

Из определения напряженности (3.6) следует, что сила, действующая на всякий точечный заряд q, в точке поля с напряженностью будет равна

. (3.9)

Если q > 0, то и сонаправлены, если q < 0, то направление векторов и противоположны.

Если поле создано системой точечных зарядов , , …, , то из принципа независимости действия сил следует, что результирующая сила , действующая со стороны исследуе-мого поля на пробный заряд , равна векторной сумме сил , приложенных к нему со стороны каждого из зарядов :

. (3.10)

Учитывая, что , , где – напряженность результирующего поля, – напряженность поля, создаваемого одним зарядом , и подставляя эти выражения в (3.10), получим принцип суперпозиции электростатических полей

, (3.11)

напряжённость E результирующего электрического поля, создаваемого системой зарядов, равна векторной сумме напряжённостей полей, создаваемых в данной точке каждым из этих зарядов в отдельности.

Принцип суперпозиции (3.11) можно использовать для расчета любых электрических полей.