7.5.4.3.Элементы теории сложности

В теории сложности выделяют массовые и индивидуальные задачи. Первые из них сформулированы в общем виде, вторые представлены с конкретными числовыми значениями исходных данных. Исследования сложности проводятся в отношении массовых задач и получаемые выводы, как правило, относятся к наихудшему случаю – к наиболее неблагоприятному возможному сочетанию исходных данных.

Цель исследований – установление вида зависимости объема Q требуемых вычислений от размера задачи N. Объем вычислений может определяться числом арифметических и логических операций или затратами процессорного времени ЭВМ с заданной производительностью. Размер задачи в общем случае связывают с объемом описания задачи, но в приложениях понятие размера легко наполняется более конкретным содержанием.

Далее, в теории сложности задач выбора вводят понятие эффективных и неэффективных алгоритмов. К эффективным относят алгоритмы с полиномиальной зависимостью Q от N, например, алгоритмы с функцией Q(N) линейной, квадратичной, кубической и др. Для неэффективных алгоритмов характерна экспоненциальная зависимость Q(N).

Важность проведения резкой границы между полиномиальными и экспоненциальными алгоритмами вытекает из сопоставления числовых примеров роста допустимого размера задачи с увеличением быстродействия Б используемых ЭВМ (табл. 7.5, в которой указаны размеры задач, решаемых за одно и то же время T на ЭВМ с быстродействием Б_i, при различных зависимостях сложности Q от размера N). Эти примеры показывают, что выбирая ЭВМ в К раз более быстродействующую, получаем увеличение размера решаемых задач при линейных алгоритмах в К раз, при квадратичных алгоритмах в K^1/2 раз и т.д.

Таблица 7.5

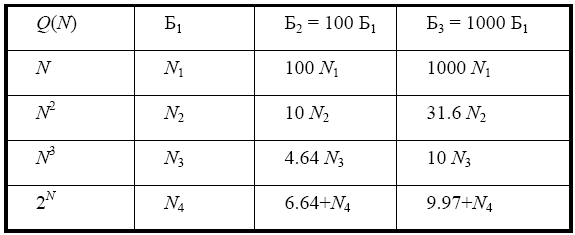
Иначе обстоит дело с неэффективными алгоритмами. Так, в случае сложности 2^N для одного и того же процессорного времени размер задачи увеличивается только на lgK/lg2 единиц. Следовательно, переходя от ЭВМ с Б = 1Gflops к суперЭВМ с Б = 1Tflops, можно увеличить размер решаемой задачи только на 10, что совершенно недостаточно для практических задач. Действительно, в таких задачах, как например, синтез тестов для БИС число входных двоичных переменных может составлять более 150 и поэтому полный перебор всех возможных проверяющих кодов потребует выполнения более 2¹⁵⁰ вариантов моделирования схемы.

В теории сложности все комбинаторные задачи разделены на классы:

• класс неразрешимых задач, в который входят массовые задачи, решение которых полным перебором принципиально невозможно с точки зрения современных научных представлений; этот класс отделяется от других задач так называемым пределом Бреммермана, оцениваемым величиной N = 10⁹³; отметим, что реальный предел неразрешимости значительно ниже;

• класс Р, к которому относятся задачи, для которых известны алгоритмы решения полиномиальной сложности;

• класс NP, включающий задачи, для которых можно за полиномиальное время проверить правильность решения, т.е. ответить на вопрос, удовлетворяет ли данное решение заданным условиям; очевидно, что Р включено в NP, однако вопрос о совпадении этих классов пока остается открытым, хотя по-видимому на этот вопрос будет получен отрицательный ответ;

• класс NP-полных задач, характеризующийся следующими свойствами: 1) для этих задач неизвестны полиномиальные алгоритмы точного решения; 2) любые задачи внутри этого класса могут быть сведены одна к другой за полиномиальное время. Последнее означает, что если будет найден полиномиальный алгоритм для точного решения хотя бы одной NP-полной задачи, то за полиномиальное время можно будет решить любую задачу этого класса.

Из результатов теории сложности следуют важные практические рекомендации: 1) приступая к решению некоторой комбинаторной задачи, следует сначала проверить, не принадлежит ли она к классу NP-полных задач, и если это так, то не следует тратить усилия на разработку алгоритмов и программ точного решения; 2) отсутствие эффективных алгоритмов точного решения массовой задачи выбора отнюдь не означает невозможности эффективного решения индивидуальных задач из класса NP-полных или невозможности получения приближенного решения по эвристическим алгоритмам за полиномиальное время.