7.3.2.Алгоритм численного интегрирования соду

Одна из удачных реализаций неявного метода второго порядка, которую можно считать модификацией метода трапеций, основана на комбиниро­ванном использовании явной и неявной формул Эйлера. Рассмотрим вопрос, почему такое комбини­рование снижает погрешность и приводит к повышению порядка метода.

Предварительно отметим, что в методах p-го порядка локальная погрешность, т.е. погрешность, допущенная на одном п-м шаге интегрирования, оценивается старшим из отбрасываемых членов

в разложении решения V(t) в ряд Тейлора, где с - постоянный коэффициент, зависящий от метода, - норма вектора (р+1)-х производных V (t), которая оценивается с помощью конечно-раз­ностной аппроксимации, – значение времени t внутри шага.

Если n-й шаг интегрирования в комбинированном методе был неявным, т.е. выполненным по не­явной формуле, то следующий шаг с тем же значением И должен быть явным. Используя разложение решения V(t) в ряд Тейлора в окрестностях точки t_n+1, получаем для (n+1)-го неявного шага

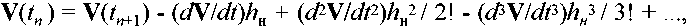
7.28

и для (п+2)-го явного шага

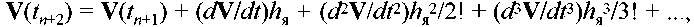
7.29

где - величины неявного и явного шагов, а значения производных относятся к моменту t_n+1.

Подставляя (7.28) в (7.29), при получаем:

т.е. погрешности, обусловливаемые квадратичными членами в (7.28) и (7.29) взаимно компенсируются, и старшим из отбрасываемых членов становится член с . Следовательно, изложенное комбини­рование неявной и явной формул Эйлера дает метод интегрирования второго порядка.

Неявные методы и, в частности, рассмотренный комбинированный метод целесообразно ис­пользовать только при переменной величине шага. Действительно, при заметных скоростях измене­ния фазовых переменных погрешность остается в допустимых пределах только при малых шагах, в квазистатических режимах шаг может быть во много раз больше.

Алгоритмы автоматического выбора шага основаны на сравнении допущенной и допустимой локальных погрешностей. Например, вводится некоторый диапазон (коридор) погрешностей δ, в пре­делах которого шаг сохраняется неизменным. Если же допущенная погрешность превышает верхнюю границу диапазона, то шаг уменьшается, если же выходит за нижнюю границу, то шаг увеличивается.

7.3.3.Методы решения систем нелинейных алгебраических уравнений

Вычисления при решении СОДУ состоят из нескольких вложенных один в другой циклических процессов. Внешний цикл -цикл пошагового численного интегрирования, параметром цикла является номер шага. Если модель анализируемого объекта нелинейна, то на каждом шаге выполняется промежуточный цикл - итера­ционный цикл решения системы нелинейных алгебраических уравнений (СНАУ). Параметр цикла - номер итерации. Во внутреннем цикле решается система линейных алгебраических уравнений (СЛАУ), например, при применении узлового метода формирования ММС такой системой является (7.19). Поэтому в математическое обеспечение анализа на макроуровне входят методы решения СНАУ и СЛАУ.

Для решения СНАУ можно применять прямые итерационные методы такие, как метод простой итерации или метод Зейделя, но в современных программах анализа наибольшее распространение по­лучил метод Ньютона, основанный на линеаризации СНАУ Собственно модель (7.19) получена имен­но в соответствии с методом Ньютона. Основное преимущество метода Ньютона - высокая скорость сходимости.

Представим СНАУ в виде

F(X)=0.

7.30

Разлагая F(Х) в ряд Тейлора в окрестностях некоторой точки X_k, получаем

Сохраняя только линейные члены, получаем СЛАУ с неизвестным вектором X:

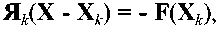
7.31

где Решение системы (7.31) дает очередное приближение к корню системы (7.30), которое удобно обозначить

Вычислительный процесс стартует с начального приближения и в случае сходимости итера­ций заканчивается, когда погрешность, оцениваемая как

станет меньше допустимой погрешности ε.

Однако метод Ньютона не всегда приводит к сходящимся итерациям. Условия сходимости метода Ньютона выражаются довольно сложно, но существует легко используемый подход к улучшению сходимости. Это близость начального приближения к искомому корню СНАУ Использование этого фактора привело к появлению метода решения СНАУ, называемого продолжением решения по параметру.

В методе продолжения решения по параметру в ММС выделяется некоторый параметр а, такой, что при корень системы (7.30) известен, а при увеличении от 0 до его истинного значения составляющие вектора X плавно изменяются от до истинного значения корня. Тогда задача разбивается на ряд подзадач, последовательно решаемых при меняющихся значениях , и при достаточно малом шаге Δα изменения α условия сходимости выполняются.

В качестве параметра α можно выбрать некоторый внешний параметр, например, при анализе электронных схем им может быть напряжение источника питания. Но на практике при интегрировании СОДУ в качестве α выбирают шаг интегрирования h. Очевидно, что при h = 0 корень СНАУ равен значению вектора неизвестных на предыдущем шаге. Регулирование значений h возлагается на алгоритм автоматического выбора шага.

В этих условиях очевидна целесообразность представления математических моделей для анали­за статических состояний в виде СОДУ, как и для анализа динамических режимов.