7.3.Методы и алгоритмы анализа на макроуровне

7.3.1.Выбор методов анализа во временной области

Анализ процессов в проектируемых объектах можно производить во временной и частотной областях. Анализ во временной области (динамический анализ) позволяет получить картину переходных процессов, оценить динамические свойства объекта, он является важной процедурой при исследовании как линейных, так и нелинейных систем. Анализ в частотной области более специфичен, его применяют, как правило, к объектам с линеаризуемыми ММ при исследовании колебательных стационарных процессов, анализе устойчивости, расчете иска­жений информации, представляемой спектральными составляющими сигналов, и т.п.

Методы анализа во временной области, используемые в универсальных программах анализа в САПР, - это численные методы интегрирования систем обыкновенных дифференциальных уравне­ний (СОДУ):

Другими словами, это методы алгебраизации дифференциальных уравнений. Формулы интегри­рования СОДУ могут входить в ММ независимо от компонентных уравнений, как это имеет место в (7.15), или быть интегрированными в ММ компонентов, как это выполнено в узловом методе.

От выбора метода решения СОДУ существенно зависят такие характеристики анализа, как точ­ность и вычислительная эффективность. Эти характеристики определяются прежде всего типом и по­рядком выбранного метода интегрирования СОДУ

Применяют два типа методов интегрирования - явные (иначе экстраполяционные или методы, основанные на формулах интегрирования вперед), и неявные (интерполяционные, основанные на формулах интегрирования назад). Различия между ними удобно показать на примере простейших ме­тодов первого порядка - методов Эйлера.

Формула явного метода Эйлера представляет собой следующую формулу замены производных в точке t_n:

где индекс равен номеру шага интегрирования; - размер шага интегрирования (обычно h называют просто шагом интегрирования). В формуле неявного метода Эйлера использовано дифференцирование назад:

где

Выполним сравнительный анализ явных и неявных методов на примере модельной задачи:

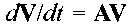
7.23

при ненулевых начальных условиях и при использовании методов Эйлера с постоянным шагом И.

Здесь А - постоянная матрица; V - вектор фазовых переменных.

При алгебраизации явным методом имеем

или

где Е - единичная матрица. Вектор V_n+1 можно выразить через вектор начальных условий V₀:

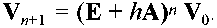
7.24

Обозначим

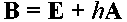
7.25

и применим преобразование подобия для матрицы В

где Т - преобразующая матрица, -диагональная матрица с собственными значениями матрицы В на диагонали. Нетрудно видеть, что

Из линейной алгебры известно, что собственные значения матриц, связанных арифметическими опе­рациями, оказываются связанными такими же преобразованиями. Поэтому из (7.25) следует

Точное решение модельной задачи (7.23) при следовательно, условием устойчивости процесса численного решения можно считать

откуда последовательно получаем поскольку и условие устойчивости

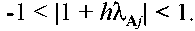
7.26

Известно, что для физически устойчивых систем собственные значения матрицы коэффициен­тов в ММС оказываются отрицательными. Если к тому же все вещественные величины (характер процессов в ММС с моделью (7.23) апериодический), то естественно определить постоянные време­ни физической системы как и условие (7.26) конкретизируется следующим образом

или

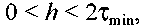
7.27

где - минимальная постоянная времени. Если использовать явные методы более высокого поряд­ка, то может увеличиться коэффициент перед в (7.27), но это принципиально не меняет оценки яв­ных методов.

Если нарушено условие (7.27), то происходит потеря устойчивости вычислений, а это означает, что в решении задачи возникают ложные колебания с увеличивающейся от шага к шагу амплитудой и быстрым аварийным остановом ЭВМ вследствие переполнения разрядной сетки. Конечно, ни о ка­кой адекватности решения говорить не приходится.

Для соблюдения (7.27) применяют те или иные алгоритмы автоматического выбора шага. Отме­тим, что в сложной модели расчет для непосредственного выбора шага по (7.27) слишком трудо­емок, кроме того, однократный расчет мало чем помогает, так как в нелинейных моделях мо­жет изменяться от шага к шагу.

Условие (7.27) накладывает жесткие ограничения на шаг интегрирования. В результате вычис­лительная эффективность явных методов резко падает с ухудшением обусловленности ММС. В самом деле, длительность моделируемого процесса должна быть соизмеримой с временем успокоения системы после возбуждающего воздействия, т.е. соизмерима с максимальной постоянной времени Требуемое число шагов интегрирования равно

Отношение называют разбросом постоянных времени или числом обусловленности. Чем больше это число, тем хуже обусловленность. Попытки применения явных методов к любым ММС чаще всего приводят к недопустимо низкой вычислительной эффективности, поскольку в ре­альных моделях - обычная ситуация. Поэтому в настоящее время в универсальных програм­мах анализа явные методы решения СОДУ не применяют.

Аналогичный анализ числовой устойчивости неявных методов дает следующие результаты. Вместо (7.24) имеем

и условие числовой устойчивости принимает вид

которое выполняется при любых h > 0. Следовательно, неявный метод Эйлера обладает так называемой А - устойчивостью.

Примечание. Метод интегрирования СОДУ называют A-устойчивым, если погрешность интегрирования оста­ется ограниченной при любом шаге h > 0.

Применение A-устойчивых методов позволяет существенно уменьшить требуемые числа шагов Ш. В этих методах шаг выбирается автоматически не из условий устойчивости, а только из соображе­ний точности решения.

Выбор порядка метода решения СОДУ довольно прост: во-первых, более высокий порядок обес­печивает более высокую точность, во-вторых, среди неявных разностных методов, кроме метода Эй­лера, A-устойчивы также методы второго порядка и среди них - метод трапеций. Поэтому преобла­дающее распространение в программах анализа получили методы второго порядка - модификации метода трапеций.