7.5.2.4.Необходимые условия экстремума

В задачах безусловной оптимизации необходимые условия представляют собой равенство нулю градиента целевой функции

grad F(X) = 0.

В общей задаче математического программирования (7.35) необходимые условия экстремума, называемые условиями Куна-Таккера, формулируются следующим образом:

Для того чтобы точка Э была экстремальной точкой выпуклой задачи математического программирования (ЗМП), необходимо наличие неотрицательных коэффициентов u_i, таких, что

ui φi(Э) = 0, i=l,2,...m;

(7.51)

и при этом соблюдались ограничения задачи, а также выполнялось условие

(7.52)

где т – число ограничений типа неравенств, L – то же равенств, коэффициенты a_j > 0.

За приведенной абстрактной формулировкой условий скрывается достаточно просто понимаемый геометрический смысл. Действительно, рассмотрим сначала случай с ограничениями только типа неравенств. Если максимум находится внутри допустимой области R, то, выбирая все u_i = 0, добиваемся выполнения (7.51); если же точка максимума Э лежит на границе области R, то, как видно из левой части рис. 7.26, эту точку всегда соответствующим подбором неотрицательных u_i можно поместить внутрь оболочки, натянутой на градиенты целевой функции F(X) и функций-ограничений φ_i(Х). Наоборот, если точка не является экстремальной, то (7.51) нельзя выполнить при любом выборе положительных коэффициентов u_i (см. правую часть рис. 7.26, где рассматриваемая точка X лежит вне выпуклой оболочки, натянутой на градиенты). Учет ограничений типа равенств очевиден, если добавляется последняя из указанных в (7.52) сумма.

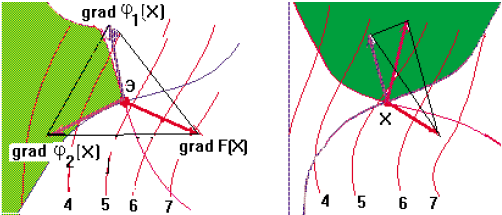
Рисунок 7.26 – К пояснению условий Куна-Таккера

7.5.2.5.Методы поиска условных экстремумов.

Широко известен метод множителей Лагранжа, ориентированный на поиск экстремума при наличии ограничений типа равенств ψ(Х) = 0, т.е. на решение задачи

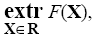
(7.53)

где R={Х | ψ(Х) = 0}.

Суть метода заключается в преобразовании задачи условной оптимизации (7.53) в задачу безусловной оптимизации с помощью образования новой целевой функции

где λ = (λ₁, λ₂, λ₃ ... λ_h) – вектор множителей Лагранжа, L – число ограничений. Необходимые условия экстремума функции Ф(Х):

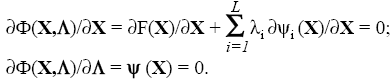
(7.54)

Система (7.54) содержит n+L алгебраических уравнений, где п – размерность пространства управляемых параметров, ее решение дает искомые координаты экстремальной точки и значения множителей Лагранжа. Однако при численном решении (7.54), что имеет место при использовании алгоритмических моделей, возникают те же трудности, что и в методе Ньютона. Поэтому в САПР основными методами решения ЗМП являются методы штрафных функций и проекции градиента.

Основная идея методов штрафных функций – преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции Ф(Х) введением в исходную целевую функцию F(X) специальным образом выбранной функции штрафа S(X):

Ф(Х)=F(Х) + rS(Х),

где r – множитель, значения которого можно изменять в процессе оптимизации.

Среди методов штрафных функций различают методы внутренней и внешней точки. Согласно методам внутренней точки ( иначе называемым методами барьерных функций) исходную для поиска точку можно выбирать только внутри допустимой области, а для методов внешней точки как внутри, так и вне допустимой области (важно лишь, чтобы в ней функции целевая и ограничений были бы оп­ределены). Ситуация появления барьера у целевой функции Ф(х) и соотношение между условным в точке х₂ и безусловным в точке x_i минимумами F(x) в простейшем одномерном случае иллюстрируется рис. 7.27.

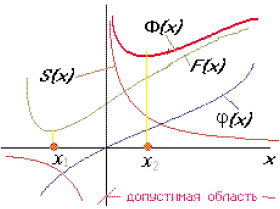
Рисунок 7.27 – Пояснение метода штрафных функций

Примеры штрафных функций:

1) для метода внутренней точки при ограничениях φ_i(Х)> О

где т – число ограничений типа неравенств;

2) для метода внешней точки при таких же ограничениях

здесь штраф сводится к включению в Ф(Х) суммы квадратов активных (т.е. нарушенных) ограничений;

3) в случае ограничений типа равенств ψ_i(Х) = 0

Чем больше коэффициент r, тем точнее решение задачи, однако при больших r может ухудшаться ее обусловленность. Поэтому в начале поиска обычно выбирают умеренные значения r, увеличивая их в окрестностях экстремума.

Основной вариант метода проекции градиента ориентирован на задачи математического программирования с ограничениями типа равенств.

Поиск при выполнении ограничений осуществляется в подпространстве (п-т) измерений, где п – число управляемых параметров, т – число ограничений, при этом движение осуществляется в направлении проекции градиента целевой функции F(X) на гиперплоскость, касательную к гиперповерхности ограничений (точнее к гиперповерхности пересечения гиперповерхностей ограничений).

Поиск минимума начинают со спуска из исходной точки на гиперповерхность ограничений. Далее выполняют шаг в указанном выше направлении (шаг вдоль гиперповерхности ограничений). Поскольку этот шаг может привести к заметному нарушению ограничений, вновь повторяют спуск на гиперповерхность ограничений и т.д. Другими cловами, поиск заключается в выполнении пар шагов, каждая пара включает спуск на гиперповерхность ограничений и движение вдоль гиперповерхности ограничений.

Идею метода легко пояснить для случая поиска в двумерном пространстве при одном ограничении ψ(Х) = 0. На рис. 7.28 это ограничение представлено жирной линией, а целевая функция – совокупностью более тонких линий равного уровня. Спуск обычно осуществляют по нормали к гиперповерхности ограничений (в данном случае к линии ограничения). Условие окончания поиска основано на сопоставлении значений целевой функции в двух последовательных точках, получаемых после спуска на гиперповерхность ограничений.

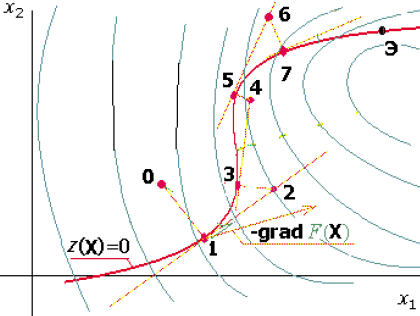
Рисунок 7.28 – Траектория поиска в соответствии с методом проекции градиента: Э - условный экстремум; 0,1,2,3 – точки на траектории поиска

Рассмотрим вопрос, касающийся получения аналитических выражений для направлений спуска и движения вдоль гиперповерхности ограничений.

Спуск. Необходимо из текущей точки поиска В попасть в точку А, являющуюся ближайшей к В точкой на гиперповерхности ограничений, т.е. решить задачу

min |B-A|

при условии ψ(Х) = 0, которое после линеаризации в окрестностях точки В имеет вид

ψ(B) + (grad ψ(B))^T(A-B) = 0.

Используя метод множителей Лагранжа, обозначая A-B=U и учитывая, что минимизация расстояния равнозначна минимизации скалярного произведения U на U, запишем

Ф(А) = U^TU + λ(ψ(B)+(grad ψ(В))^TU);

dФ/dА = 2U + λ(grad ψ(В)) = 0;	(7.55)
dФ/dλ, = ψ(В) + (grad ψ(В))TU = 0.	(7.56)

Тогда из (7.55) получаем выражение

U = - 0,5λ (grad ψ(В)),

подставляя его в (7.65), имеем

ψ(В) - 0,5λ (grad ψ(В))^Т grad ψ(В)= 0;

откуда

λ = (0,5(grad ψ(В))^T grad ψ(В))^-1 ψ(В).

и окончательно, подставляя А в (7.55), находим

U = - grad ψ(В) (grad ψ(В))^T grad ψ(В))^-1 ψ(В).

Движение вдоль гиперповерхности ограничений. Шаг в гиперплоскости D, касательной к гиперповерхности ограничений, следует сделать в направлении вектора S, на котором целевая функция уменьшается в наибольшей мере при заданном шаге h. Уменьшение целевой функции при переходе из точки А в новую точку С подсчитывают, используя формулу линеаризации F(X) в окрестностях точки А:

F(C) - F(A) = h(grad F(A))^TS,

где grad F(A)^TS – приращение F(X), которое нужно минимизировать, варьируя направления S

min F(C) = min ((grad F(A))TS),

(7.57)

где вариация S осуществляется в пределах гиперплоскости D; gradψ(A) и S – ортогональные векторы. Следовательно, минимизацию (7.57) необходимо выполнять при ограничениях

(grad ψ(A))^TS = 0,

S^TS=1.

Последнее ограничение говорит о том, что при поиске направления движения, вектор S должен лишь указывать это направление, т.е. его длина несущественна (пусть S – единичный вектор). Для решения (7.57) используем метод множителей Лагранжа

Ф(S, λ,q) = (grad F(A))^TS + λ(grad ψ(A))^TS + q(S^TS - 1),

где λ и q – множители Лагранжа;

dФ/dS = grad F(A) + λ grad ψ(A) + qS = 0;	(7.58)
dФ/dλ, = (grad ψ(A))TS = 0;	(7.59)
dФ/dq = STS-1 = 0.	(7.60)

Из (7.58) следует, что

S = -(grad F(A) + λ grad ψ (A) )/q

подставляя S в (7.59), получаем

(grad ψ(A))^Tgrad F(A) + λ (grad ψ(A))^Tgrad ψ(A) = 0,

откуда

(7.61)

Таким образом, матрица

P = E - grad ψ(A)[(grad ψ(A))^Tgrad ψ(A)]^-1 grad ψ(A))^T

представляет собой проектирующую матрицу, а вектор S, рассчитанный по (7.61), – проекцию градиента grad F(A) на гиперповерхность ограничений.

Частным случаем применения метода проекции градиента являются задачи оптимизации с максиминным критерием. Действительно, для поиска экстремума функции минимума

где Z_j - нормированная величина j-го выходного параметра y_j удобно применять метод проекции градиента. В качестве ограничений задачи в исходной постановке фигурируют только прямые ограничения

x_{max i}>x_i>x_{min i}

Здесь x_{max i} и x_{min i} – граничные значения допустимого диапазона варьирования параметра х_i. В процессе поиска, если минимальной является функция Z_q(X) и траектория поиска пересекает гребень

Zq(X) - Zk(X) = 0,

(7.62)

то поиск продолжается в направлении проекции градиента функции Z_q(X) на гиперповерхность гребня (7.62).