7.2.6.Узловой метод

Матрицу контуров и сечений М в узловом методе формируют следующим об­разом. Выбирают базовый узел эквивалентной схемы и каждый из остальных узлов соединяют с ба­зовым фиктивной ветвью. Именно фиктивные ветви принимают в качестве ветвей дерева, а все реаль­ные ветви оказываются в числе хорд. Поскольку токи фиктивных ветвей равны нулю, а вектор напря­жений фиктивных ветвей есть вектор узловых потенциалов φ, то уравнения (7.13) и (7.14) принимают вид

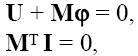
	7.16
	7.17

где U и I- векторы напряжений и токов реальных ветвей.

Компонентные уравнения алгебраизуются с помощью одной из формул численного интегриро­вания, линеаризуются с помощью разложения в ряд Тейлора с сохранением только линейных членов, и их представляют в виде

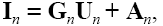
7.18

где G_n – диагональная матрица проводимостей, рассчитанная в точке t_n; А_n – вектор, зависящий от значений фазовых переменных на предшествующих шагах интегрирования и потому уже известный к моменту времени t_n. Каждая ветвь (за исключением идеальных источников напряжения) имеет проводимость, которая занимает одну из диагональных клеток матрицы проводимостей.

Окончательно ММС получаем, подставляя (7.18) и затем (7.16) в (7.17):

или

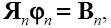
7.19

где Я_n=М^т G_nM – матрица Якоби, В_n = М^ТА_n – вектор правых частей. Отметим, что матрица М име­ет размер равен α х (β-1), матрица G_n – α х α, а матрица Якоби – (β-1) х (β-1).

Система (7.19) является системой линейных алгебраических уравнений, полученной в результате дискретизации независимой переменной, алгебраизации дифференциальных уравнений и линеаризации алгебраических уравнений. Алгебраизация приводит к необходимости пошагового вычисли­тельного процесса интегрирования, линеаризация – к выполнению итерационного вычислительного процесса на каждом шаге интегрирования.

Рассмотрим, каким образом определяются проводимости ветвей.

Для резистивных ветвей проводимость – величина, обратная сопротивлению R.

При использовании неявного метода Эйлера проводимость емкостной ветви получается из ее компонентного уравнения следующим образом.

На n-м шаге интегрирования

проводимость и при С = const получаем

При этом в вектор правых частей входит элемент

Проводимость индуктивной ветви можно найти аналогично: и при L = const

Аналогично определяют проводимости и при использовании других разностных формул чис­ленного интегрирования, общий вид которых , где μ_n зависит от шага интегрирования, η_n - от значений вектора U на предыдущих шагах.

Классический вариант узлового метода имеет ограничения на применение. Так, недопустимы идеальные (с бесконечной проводимостью) источники напряжения, зависимые источники, аргумента­ми которых являются токи, а также индуктивности, поскольку в классическом варианте токи не вхо­дят в число базисных переменных. Устранить эти ограничения довольно просто – нужно расширить совокупность базисных координат, включив в нее токи-аргументы зависимых источников, а также то­ки ветвей индуктивных и источников напряжения. Полученный вариант метода называют модифици­рованным узловым методом.

Согласно модифицированному узловому методу, в дерево при построении матрицы М включают ветви источников напряжения и затем фиктивные ветви. В результате матрица М принимает вид (табл. 7.2), где введены обозначения: U_ИCT(I) – источники напряжения, зависящие от тока; Е(t) – независимые источники напряжения; I_ИСТ(I) – источники тока, зависящие от тока; L – индуктивные ветви; M_ij – подматрица контуров хорд группы i и сечений фиктивных ветвей группы j.

Таблица 7.2 – М-матрица

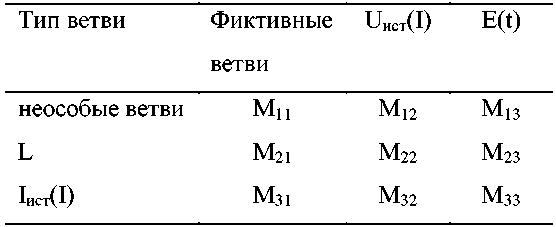
Те же обозначения U_ИCT, I, Е, I_ИСТ будем использовать и для соответствующих векторов напряжении и токов. Назовем ветви, токи которых являются аргументами в выражениях для зависимых источников, т.е. входят в вектор I, особыми ветвями. Остальные ветви (за исключением индуктивных) – неособые. Введем также обозначе­ния: I_L – вектор индуктивных токов; i_Х и U_X векторы токов и напряжений неособых ветвей; G_X, G_L, G_I – диагональные матрицы проводимостей ветвей неособых, индуктивных, особых.

Уравнение закона токов Кирхгофа (7.17) для фиктивных ветвей имеет вид ]

Исключим вектор I_Х с помощью компонентного уравнения (7.18), а вектор I_ИСТ с помощью очевидного выражения

I_ИСТ = KI,

Где – матрица передаточных коэффициентов источников тока. Используем также выражение (7.16), принимающее вид

Получаем систему из трех матричных уравнений с неизвестными векторами φ, I и I_L:

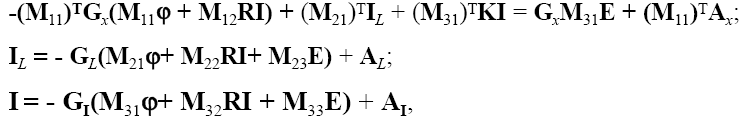
	7.20
	7.21
	7.22

где обозначено R=(δU_ист/δI) Эта система и является итоговой ММ в узловом модифицированном методе.

Замечания:

1. Вектор индуктивных токов нельзя исключить из итоговой системы уравнений, так как его значения входят в вектор A_L на последующих шагах численного интегрирования.

2. Источники тока, зависящие от напряжений, относятся к неособым ветвям, их проводимости 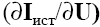входят в матрицу G_x, которая при этом может иметь недиагональный вид.

3. Источники напряжения, зависящие от напряжений, в приведенных выше выражениях не учитываются, при их наличии нужно в матрице М выделить столбец для этих ветвей, что приводит к появлению дополнительных слагаемых в правых частях уравнений (7.19) – (7.21).