7.3.4.Методы решения систем линейных алгебраических уравнений

В программах анализа в САПР для решения СЛАУ чаще всего применяют метод Гаусса или его разновидности. Метод Гаусса - метод последовательного исключения неизвестных из системы уравнений. При исключении k-й неизвестной из системы уравнений

AX = B

7.32

все коэффициенты a_ij при i>к и j>k пересчитывают по формуле

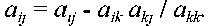
7.33

Исключение п-1 неизвестных, где п - порядок системы (7.32), называют прямым ходом, в процессе которого матрица коэффициентов приобретает треугольный вид. При обратном ходе последовательно вычисляют неизвестные, начиная с x_n.

В общем случае число арифметических операций для решения (7.32) по Гауссу пропорционально . Это приводит к значительным затратам машинного времени, поскольку СЛАУ решается многократно в процессе одновариантного анализа, и существенно ограничивает сложность анализируемых объектов.

Заметно повысить вычислительную эффективность анализа можно, если использовать характерное практически для всех приложений свойство высокой разреженности матрицы А в модели (7.32).

Матрицу называют разреженной, если большинство ее элементов равно нулю. Эффективность обработки разреженных матриц велика потому, что, во-первых, пересчет по формуле (7.33) не требуется, если хотя бы один из элементов a_ik или a_kj оказывается нулевым, во-вторых, не требуются затраты памяти для хранения нулевых элементов. Хотя алгоритмы обработки разреженных матриц более сложны, но в результате удается получить затраты машинного времени, близкие к линейным, например, затраты оказываются пропорциональными .

При использовании методов разреженных матриц нужно учитывать зависимость вычислительной эффективности от того, как представлена матрица коэффициентов А, точнее от того, в каком порядке записаны ее строки и столбцы.

Для пояснения этой зависимости рассмотрим два варианта представления одной и той же СЛАУ В первом случае система уравнений имеет вид

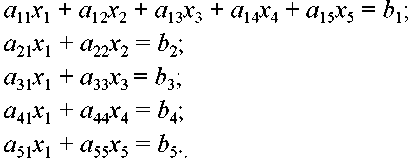
При прямом ходе в соответствии с формулой (7.33) все элементы матрицы, которые первоначально были нулевыми, становятся ненулевыми, а матрица оказывается полностью насыщенной. Элементы, становящиеся ненулевыми в процессе гауссовых исключений, называют вторичными ненулями.

Таблица 7.3

Вторичные ненули в таблице 7.3 отмечены точкой. Во втором случае меняются местами первое и пятое уравнения. Матрицы коэффициентов имеют вид таблиц 7.3 и 7.4, где ненулевые элементы представлены знаком +. Теперь вторичные ненули не появляются, матрица остает­ся разреженной, высокая вычислительная эффективность сохраняется.

Таблица 7.4

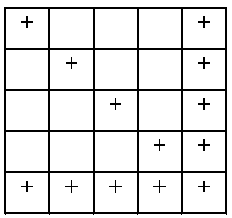
Таким образом, методы разреженных матриц должны включать в себя способы оптимального упорядочения строк и столбцов матриц. Используют несколько критериев оптимальности упорядочения. Простейшим из них является критерий расположения строк в порядке увеличения числа первичных ненулей, более сложные критерии учитывают не только первичные ненули, но и появляющиеся вторичные ненули.

Методом разреженных матриц называют метод решения СЛАУ на основе метода Гаусса с учетом разреженности (первичной и вторичной) матри­цы коэффициентов.

Метод разреженных матриц можно реализовать путем интерпретации и компиляции. В обоих случаях создаются массивы ненулевых коэффициентов матрицы (с учетом вторичных ненулей) и массивы координат этих ненулевых элементов.

При этом выигрыш в затратах памяти довольно значителен. Так, при матрице умеренного размера 200x200 без учета разреженности потребуется 320 кбайт Если же взять характерное значение 9 для среднего числа ненулей в одной строке, то для коэффициентов и указателей координат потребуется не более 28 кбайт.

В случае интерпретации моделирующая программа для каждой операции по (7.33) при a_ik ≠ 0 и a_kj ≠ 0 находит, используя указатели, нужные коэффициенты и выполняет арифметические операции по (7.33). Поскольку СЛАУ в процессе анализа решается многократно, то и операции поиска нужных коэффициентов также повторяются многократно, на что естественно тратится машинное время.

Способ компиляции более экономичен по затратам времени, но уступает способу интерпретации по затратам памяти. При компиляции поиск нужных для (7.33) коэффициентов выполняется однократ­но перед численным решением задачи. Вместо непосредственного выполнения арифметических опе­раций для каждой из них компилируется команда с найденными адресами ненулевых коэффициентов. Такие команды образуют рабочую программу решения СЛАУ, которая и будет решаться многократно. Очевидно, что теперь в рабочей программе будет выполняться минимально необходимое число арифметических операций.