
- •Лекция 1
- •Закон полного тока и закон электромагнитной индукции в дифференциальной форме.
- •Полная система уравнений электромагнитного поля в дифференциальной форме.
- •Граничные условия
- •На поверхности раздела диэлектриков.
- •На поверхности раздела проводника и диэлектрика.
- •Теоремы Остроградского – Гаусса и Стокса.
- •Лекция 2 Электростатическое поле
- •Уравнения Пуассона и Лапласа.
- •Лекция 3
- •Применение функций комплексного переменного.
- •Метод заданного комплексного потенциала.
- •Лекция 4 Метод зеркальных изображений.
- •Метод конформных отображений.
- •Графический метод построения картины плоскопараллельного поля.
- •Электрическое поле в диэлектрике около проводников с постоянными токами.
- •Электрическое поле постоянных токов в проводящей среде.
- •Аналогия электрического поля постоянных токов и электростатического поля. Метод электростатической аналогии.
- •Расчёт сопротивления заземления
- •Моделирование электростатических полей полем постоянного тока в проводящей среде
- •Лекция 7
- •Плоскопараллельное магнитное поле.
- •Комплексный потенциал магнитного поля.
- •Магнитное поле двух нитей с прямым и обратным током.
- •Принцип соответствия плоскопараллельных электрических и магнитных полей.
- •Граничные условия в магнитном поле у поверхности ферромагнетиков.
- •Метод зеркальных изображений в магнитном поле.
- •Графический метод построения картины плоскопараллельного магнитного поля.
- •Приближенные методы расчёта и построения картины плоскопараллельного поля. Метод сеток.
- •Лекция 8 Векторный потенциал магнитного поля.
- •Случай линейных проводником с током.
- •Определение магнитного потока через векторный потенциал.
- •Расчёт индуктивностей.
- •Лекция 9 Индуктивность коаксиального кабеля.
- •Индуктивности тонких проводников с токами
- •Лекция 10 Метод участков.
- •Индуктивности систем параллельных проводов.
- •Взаимная индуктивность между двумя двухпроводными линиями.
- •Две двухпроводные линии, расположенные симметрично в параллельных плоскостях.
- •Линии расположены во взаимно перпендикулярных плоскостях.
- •Индуктивность трёхфазной линии.
- •Лекция 11 Переменное электромагнитное поле в диэлектрике
- •Вектор Умова-Пойнтинга.
- •Длина электромагнитной волны в диэлектрике.
- •Лекция 12 Переменное электромагнитное поле в проводящей среде.
- •Длина волны и затухание.
- •Понятие об электромагнитном экранировании.
- •Лекция 13
- •Активное сопротивление шины для переменного тока.
Метод конформных отображений.
Расчёт поля методом конформных отображений основан на том, что существует возможность отобразить с помощью некоторого математического преобразования заданную область в комплексной плоскости « z » (x + jy) на так называемую каноническую область в комплексной плоскости « ω » ( ξ+j).
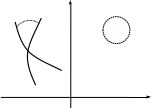
В качестве канонической области обычно используется верхняя полуплоскость, а также круг либо полоса. Преобразование называется конформным, так как при переходе от одной области к другой либо обратно сохраняются углы в точках пересечения между любыми линиями в обеих областях z = ω (рис.4-3).
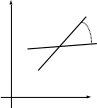

 jy j
jy j
z ω
1 z 1 2
ω
2
zk ωk
x ξ
Рисунок 4–3
Для изучения полей это очень важно, так как мы знаем, что линии равного потенциала и линии напряжённости всегда пересекаются под прямым углом.
Существует общий подход к преобразованию произвольной многоугольной области, ограниченной ломаной линией на верхнюю полуплоскость и обратно с помощью интеграла Кристоффеля-Шварца.
Для многих часто встречающихся конфигураций областей получены соотношения, необходимые для преобразования, они приведены в справочной литературе. Рассмотрим некоторые простые примеры.
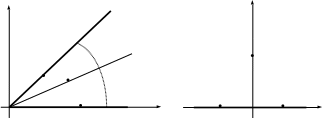
1. Двугранный угол () – поле между двумя проводящими плоскостями, сходящимися под углом (рис. 4–4а).
 jy
j
jy
j
 z
z
U = 0 ω
C
B C
A U = 0 x B A ξ
0 а) 0 б)
Рисунок 4–4
 Проводящие
грани имеют одинаковый потенциал (U
= 0), совместим
ось (x)
со следом одной из граней. Преобразование
такой области на верхнюю полуплоскость
(ω) осуществляется по формуле:
Проводящие
грани имеют одинаковый потенциал (U
= 0), совместим
ось (x)
со следом одной из граней. Преобразование
такой области на верхнюю полуплоскость
(ω) осуществляется по формуле:
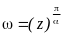
Положение любой
точки на первой грани (точка А),
координаты которой в исходной системе
координат записываются в виде:
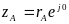 ,
в области ω определяется координатой
,
в области ω определяется координатой
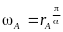 и располагаются на положительной части
вещественной оси ξ. (рис. 4–3б). Изменяется
лишь линейный масштаб. Положение любой
точки на второй грани (точка B),
координаты которой в исходной системе
координат записываются в виде:
и располагаются на положительной части
вещественной оси ξ. (рис. 4–3б). Изменяется
лишь линейный масштаб. Положение любой
точки на второй грани (точка B),
координаты которой в исходной системе
координат записываются в виде: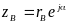 ,
в области ω определяется координатой
,
в области ω определяется координатой
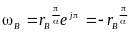 и располагаются на отрицательной части
вещественной оси ξ. Положение любой
точки на биссектрисе угла (точка С),
координаты которой в исходной системе
координат записываются в виде:
и располагаются на отрицательной части
вещественной оси ξ. Положение любой
точки на биссектрисе угла (точка С),
координаты которой в исходной системе
координат записываются в виде:
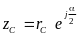 ,
в области ω определяется координатой
,
в области ω определяется координатой
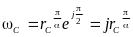 и располагаются на мнимой оси j
(см. рис.4–4б).
и располагаются на мнимой оси j
(см. рис.4–4б).
2. Бесконечно глубокий проводящий паз, шириной (d) (рисунок 4–5а).
 jy j
jy j

A F D z ω
E
E F
d
x ξ
B 0 C A B 0 C D
а) б)
Рисунок 4–5
 Пометим
начало координат посредине дна паза и
направим ось (x)
вдоль дна вправо. Преобразование такой
области на верхнюю полуплоскость (ω)
осуществляется по формуле:
Пометим
начало координат посредине дна паза и
направим ось (x)
вдоль дна вправо. Преобразование такой
области на верхнюю полуплоскость (ω)
осуществляется по формуле:
 .
.
Положение угловых
точек (В и
С), координаты
которых в исходной системе координат
записывается в виде:
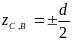 ,
в области ω также расположены на
вещественной оси ξ и определяется
координатами:
,
в области ω также расположены на
вещественной оси ξ и определяется
координатами:
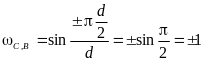 .
.
Положение точек
(A
и
D),
координаты которых в исходной системе
координат записывается в виде:
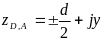 ,
в области ω расположены на вещественной
оси ξ и определяется координатами:
,
в области ω расположены на вещественной
оси ξ и определяется координатами:
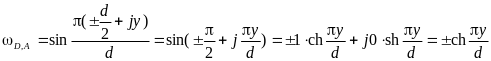 .
.
Положение точки
(E),
координата которой в исходной системе
записывается в виде:
 ,
в области ω расположена на мнимой оси
j
и определяется координатой:
,
в области ω расположена на мнимой оси
j
и определяется координатой:
 . (см. рис.4–5б).
. (см. рис.4–5б).
3. Плоскость с вертикальным выступом (стеной), высотой (h) (рисунок 4–6а).
 jy j
jy j
B z ω
C B ω0
z0
h
x ξ
A 0 D A 0 C 0 D
а) б)
Рисунок 4–6
 Начало
координат поместим у основания выступа
и направим ось (x)
вдоль горизонтальной плоскости.
Преобразование такой области на верхнюю
полуплоскость (ω) осуществляется по
формуле:
Начало
координат поместим у основания выступа
и направим ось (x)
вдоль горизонтальной плоскости.
Преобразование такой области на верхнюю
полуплоскость (ω) осуществляется по
формуле:
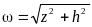 .
.
Положение точки
(С),
координата которой в исходной системе
записывается в виде:
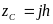 ,
в области ω расположена в начале
координат, так как определяется
координатой:
,
в области ω расположена в начале
координат, так как определяется
координатой:
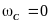 .
Положение точки (0),
координата которой в исходной системе
записывается в виде:
.
Положение точки (0),
координата которой в исходной системе
записывается в виде:
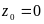 ,
в области ω вследствие двузначности
корня даёт два значения на вещественной
оси ξ и определяется координатами:
,
в области ω вследствие двузначности
корня даёт два значения на вещественной
оси ξ и определяется координатами:
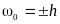 .
Положение точек (A
и D),
координаты которых в исходной системе
записывается в виде:
.
Положение точек (A
и D),
координаты которых в исходной системе
записывается в виде:
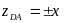 ,
в области ω расположены на вещественной
оси ξ и определяется координатами:
,
в области ω расположены на вещественной
оси ξ и определяется координатами:
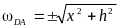 Положение точки (B),
координата которой в исходной системе
записывается в виде:
Положение точки (B),
координата которой в исходной системе
записывается в виде:
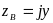 (y>h),
в области ω расположена на мнимой оси
j
и определяется координатой:
(y>h),
в области ω расположена на мнимой оси
j
и определяется координатой: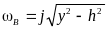 (см.
рис.4–6б).
(см.
рис.4–6б).
Получение выражения для комплексного потенциала в исходной области на плоскости (z) и определение зависимости плотности заряда () на поверхности проводников рассмотрим на примере плоскости с выступом.
Пусть в исходной
системе заряженный провод с зарядом
(+)
находится в точке с координатой (z0
= x0
+ jy0).
После преобразования исходной области
на каноническую область на основе
используемой формулы преобразования
найдём место расположения заряженного
провода в области ω (рис.4-6):
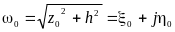 . Затем, используя метод зеркальных
изображений, заменим проводящую среду
диэлектриком с проницаемостью
и с зеркально расположенным зарядом
(–)
. Его координата является сопряжённой
с координатой исходного заряда:
. Затем, используя метод зеркальных
изображений, заменим проводящую среду
диэлектриком с проницаемостью
и с зеркально расположенным зарядом
(–)
. Его координата является сопряжённой
с координатой исходного заряда:
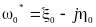 .
.
Запишем известное выражение для комплексного потенциала в системе двух заряженных осей (проводов).
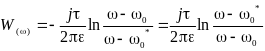 ,
,
здесь ω – координата произвольной точки поля. В области ω линии равного потенциала и линии напряжённости являются, как мы уже знаем, окружностями. Для перехода к исходной области выразим ω через z, тогда получим:
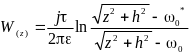 .
.
Величину напряжённости в любой точке определяем через производную от комплексного потенциала:
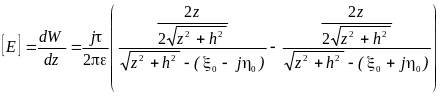 .
.
После упрощения получим:
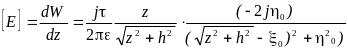 .
.
Подставляя координаты поверхности проводников и умножая на , получим значения поверхностной плотности заряда на поверхности проводников: = D = E .
