Индуктивность трёхфазной линии.

Векторный потенциал в системе из трех проводов с параллельными и одинаково направленными токами в любой точке равен:

,

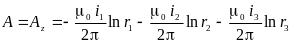причём сумма всех токов равна нулю (i₁+ i₂+i₃= 0) даже при отсутствии симметрии в системе токов.

Векторный потенциал в различных точках около проводов имеет различную начальную фазу. В связи с этим магнитные потоки, сцепленные с отдельными проводами трёхфазной линии, не совпадают по фазе с токами в этих проводах, что приводит к перераспределению нагрузки между проводами и к переносу мощности между ними.

Покажем это, рассматривая уравнения трёхфазной линии в комплексной форме:

.

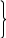
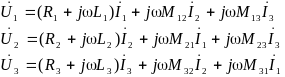В симметричной системе токов прямой последовательности токи сдвинуты на 120⁰:

; ; ,

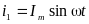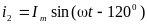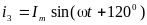Учитывая симметрию системы токов: 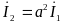; 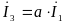, получим:

I₁

.

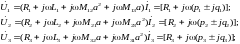
I₃ I₂

Вещественные слагаемые в скобках различны, что свидетельствует о различных значениях активной мощности, потребляемой в разных проводах линии.

При использовании транспозиции проводов трёхфазная линия становится симметричной, потому: M₁₂ = M₁₃ = M₂₃ = M, L₁ = L₂ = L₃ = L и R ₁ = R ₂ = R ₃ = R. В этом случае уравнения для различных фаз становятся идентичными:

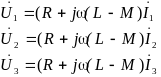
В любом проводе сдвиг фаз между током и напряжением одинаков, что позволяет исключить перенос мощности между проводами линии.

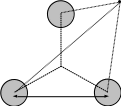
Рассмотрим трёхфазную линию, провода которой расположены в вершинах равностороннего треугольника (рис.10–8): При таком расположении проводов линия симметрична без их транспозиции, если вблизи нет ферромагнитных поверхностей.

1 r₁ m

r₃ r₂

r₀

r₀ r₀

D

2 3

Рисунок 10–8

В рассматриваемой системе векторный потенциал равен нулю в бесконечности (при r_k -> ) и в центре симметрии ( r_k = r₀), так как сумма токов в скобках равна нулю:

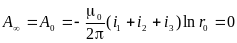
Векторный потенциал на поверхности провода первой фазы, учитывая симметрию системы токов (i₂ + i₃ = – i₁), равен:

.

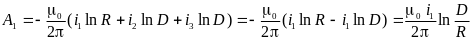Определим внешний магнитный поток первой фазы, а затем индуктивность первой фазы, равную (из-за симметрии системы) индуктивности любой фазы:

; .

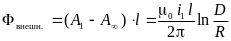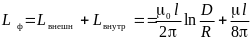Лекция 11 Переменное электромагнитное поле в диэлектрике

В переменном электромагнитном поле наблюдаются одновременно обе, рассмотренные ранее нами в отдельности, его стороны. Связь между ними дают первое и второе уравнения Максвелла – закон полного тока и закон электромагнитной индукции:

, .

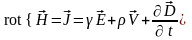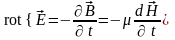Анализируя переменное электромагнитное поле в диэлектрике, считаем диэлектрик идеальным (=0) и предполагаем отсутствие в нем объёмных зарядов (=0). Тогда:

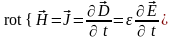
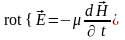
Запишем оба уравнения в проекциях на оси декартовой системы координат:

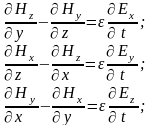
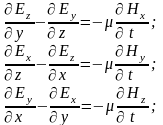
Рассмотрим случай плоско поляризованной электромагнитной волны, в которой все характеризующие её величины зависят только от одной из координат (z), а от остальных координат (x, y) не зависят. Такой характер имеют электромагнитные волны, излучаемые антенной, на больших (z>>) расстояниях от антенны, где  - длина электромагнитной волны в диэлектрике. Часто такую волну называют плоской.

В плоской электромагнитной волне производные от любых проекций векторов поля по координатам x и y равны нулю, поэтому система уравнений упрощается и принимает вид:

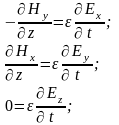
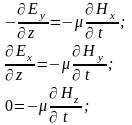
Из последних уравнений каждой системы ввиду равенства нулю производных получаем, что проекции векторов E_z и H_z не зависят от времени: E_z=const и H_z=const. Принимаем их равными нулю, так как переменное поле, излучённое антенной, не содержит постоянных составляющих. Кроме того, мы уже рассматривали ранее постоянные электрические и магнитные поля, и в случае необходимости можем, если потребуется учесть их вместе с переменным полем, применив принцип наложения.

Рассматривая оставшиеся четыре уравнения для проекций, направим ось x декартовой системы координат вдоль вектора напряжённости электрического поля (E_y=0). В этом случае остаётся единственная составляющая вектора напряжённости электрического поля: E=E_x. В этом случае уравнения ещё больше упрощаются:

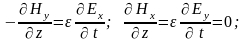
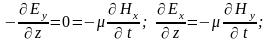
Из полученных уравнений следует, что 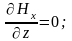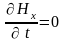, т.е. 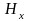=const=0,

и при выбранном направлении осей координат, вектор напряжённости магнитного поля имеет лишь единственную составляющую, направленную вдоль оси y: H=H_y. Это означает, что в плоско поляризованной электромагнитной волне в диэлектрике в любой точке векторы напряжённости электрического и магнитного поля расположены взаимно перпендикулярно.

Н айдём решение системы двух оставшихся уравнений:

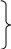
Дифференцируя первое уравнение по времени, а второе по координате z, получим:

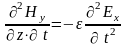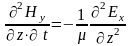; , откуда: , и обозначив 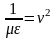, запишем уравнение для вектора напряжённости электрического поля, которое называется волновым уравнением:

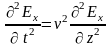
При рассмотрении режимов в цепях с распределёнными параметрами нами были получены аналогичные уравнения для напряжения в произвольной точке линии без потерь, в которой координата x отсчитывается от начала линии:

.

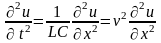Решение для волнового уравнения в линии мы получили в виде суммы прямой и обратной бегущих волн напряжения:

u = u_ + u_ = u^/(x-vt) + u^//(x+vt).

Решение для напряжённости электрического поля запишем по аналогии:

E_x = E^/(z-vt) + E^//(z+vt).

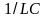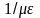Коэффициенты и в обоих уравнениях имеют одинаковые размерности, так как в цепях с распределёнными параметрами эти параметры задаются на единицу длины линии:

[L] = [] = Гн/м; [C] = []= Ф/м

Выражение для волн тока в линии мы получали с помощью волнового сопротивления:

,

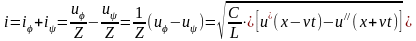здесь через Z обозначено волновое сопротивление линии без потерь, которое по аналогии эквивалентно волновому сопротивлению идеального диэлектрика для электромагнитных волн:

.

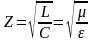Применив аналогичное преобразование для решения волнового уравнения относительно напряжённости электрического поля, получим решения для напряжённости магнитного поля:

.

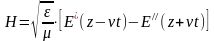Полученные решения означают, что векторы E и H в любой точке переменного электромагнитного поля взаимно перпендикулярны, связаны между собой через волновое сопротивление, а электромагнитные волны распространяются в диэлектрике со скоростью v, которая называется скоростью света и в пустоте равна:

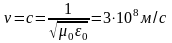
В любых диэлектриках ≥₀ и ≥₀, поэтому скорость распространения электромагнитных волн в них меньше или равна скорости света в пустоте vc.

Волновое сопротивление, связывающее между собой напряжённости электрического и магнитного поля в прямой и обратной волнах:

,

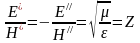также зависит от свойств диэлектрика и для пустоты равно:

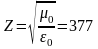Ом

Для прямой (или обратной) волны в отдельности можем записать соотношение:

; ; .

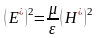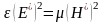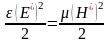Это означает, что плотности энергии электрического и магнитного поля в любой точке для прямой (или обратной) электромагнитной волны равны друг другу:

.

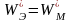Для электромагнитных волн в идеальном диэлектрике можно использовать по аналогии все ранее полученные соотношения для бегущих волн в однородной линии без потерь. В частности, справедливы формулы для определения отражённой и преломлённой волн на границе диэлектриков с различными волновыми сопротивлениями. При этом соблюдаются все граничные условия для составляющих векторов напряжённости электрического и магнитного поля. Вообще, решение волнового уравнения может быть получено, если заданы граничные и начальные условия для векторов.