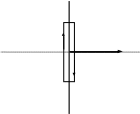
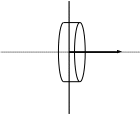
2. На поверхности раздела проводника и диэлектрика.

₁ ₂ ₁ ₂

E₁ (D₁) = 0 E₂ (D₂) D₂

а) б)

Рисунок 2

В статическом поле заряды располагаются на поверхности проводника ( ≠ 0), поэтому внутри проводника поле отсутствует (E₁ = 0, D₁ = 0). Используя соотношения, полученные выше можем записать:

; ; .

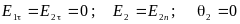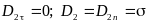В электростатическом поле векторы напряжённости и смещения перпендикулярны поверхности проводника.

Граничные условия в электрическом поле токов.

На границе раздела двух сред с различными удельными электрическими проводимостями, применяя аналогично рассмотренному выше закон электромагнитной индукции и принцип непрерывности электрического тока, можем записать:

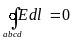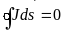и ; откуда ; ; ;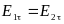

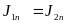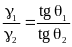На поверхности раздела сред с различными удельными электрическими проводимостями равны касательные (по отношению к границе) составляющие векторов напряжённости электрического поля и нормальные составляющие векторов плотности электрического тока.

Граничные условия в магнитном поле.

На границе раздела двух сред с различными магнитными проницаемостями, применим аналогично рассмотренному выше закон полного тока и принцип непрерывности магнитного потока:

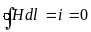, считаем, что по поверхности раздела магнетиков не протекает электрический ток. . Запишем граничные условия на поверхности раздела магнетиков:

; ; .

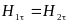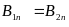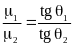На поверхности раздела сред с различными магнитными проницаемостями равны касательные (по отношению к границе) составляющие векторов напряжённости магнитного поля и нормальные составляющие векторов индукции магнитного поля.

Теоремы Остроградского – Гаусса и Стокса.

Теорема Остроградского – Гаусса позволяет преобразовать объёмный интеграл в поверхностный, а теорема Стокса – поверхностный интеграл в линейный для произвольных функций, непрерывных вместе со своими первыми производными в исследуемых областях. Эти теоремы известны из математики, и мы их только проиллюстрируем на примере уравнений электромагнитного поля.

Запишем выражение для электрического заряда в некоторой области V, ограниченной замкнутой поверхностью S, и применим постулат Максвелла к левой и правой части этого уравнения:

; ;

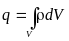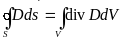Теорема Остроградского – Гаусса: Интеграл от дивергенции вектора D по некоторому объёму равен интегралу от вектора D по замкнутой поверхности, ограничивающей этот объем.

Используя выражение для электрического тока через некоторую поверхность S , ограниченную контуром l , и применив закон полного тока к обеим частям этого уравнения, получим:

; ;

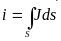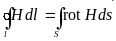Теорема Стокса: Интеграл от ротора вектора H по некоторой поверхности равен интегралу от вектора H по замкнутому контуру, ограничивающему эту поверхность.

Лекция 2 Электростатическое поле

Электростатическое поле создаётся неподвижными (по отношению к наблюдателю) электрическими зарядами. В таком поле отсутствуют электрические токи (J=0), а, следовательно, (при отсутствии намагниченных тел) и магнитное поле (H=0; B=0).

Из полной системы уравнений электромагнитного поля для электростатического поля получаем:

; ;

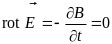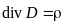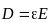
(в изотропной среде направления векторов совпадают).

В реальных устройствах объёмные заряды в диэлектрике не могут находиться в покое, т.е. появляются электрические токи, что нарушат статичность поля. Поэтому во многих случаях второе уравнение имеет нулевую правую часть:

.

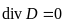Из-за равенства нулю ротора вектора напряжённости электрического поля такое поле называют безвихревым.

Применяя теорему Стокса к первому уравнению, можем записать:

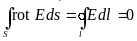
Последнее соотношение определяет независимость интеграла между фиксированными точками от пути интегрирования.

Поэтому для анализа электростатического поля удобно ввести вспомогательную скалярную функцию, называемую электрическим потенциалом. Потенциал некоторой точки поля определяется как интеграл от этой точки до точки нулевого потенциала от скалярного произведения векторов E и dl:

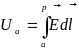
Потенциал точки определяется с точностью до некоторой произвольной постоянной, зависящей от выбора координат точки «p» – точки нулевого потенциала. Разность потенциалов между двумя точками не зависит от выбора точки нулевого потенциала и, конечно, от пути интегрирования.

.

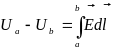При выбранном и фиксированном положении точки нулевого потенциала потенциал точки «а» зависит от координат этой точки, т.е. U_a = U (x,y,z).

Обозначим криволинейную переменную координату точки «а», лежащей на некотором расстоянии от начала координат через l_а = l, а фиксированную координату точки нулевого потенциала – через l _p (см. рисунок 2-1). Запишем выражение для потенциала точки с координатой l:

.

Дифференцируя полученное соотношение по переменному нижнему пределу, получим:

.

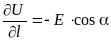p

E



dl

l_a a

l_p

0

Рисунок 2–1

Скорость изменения потенциала вдоль некоторого направления равна проекции вектора напряжённости электрического поля на это направление со знаком минус.

Так как потенциал точки «а» не зависит от пути интегрирования, то, проводя кривую «l» через точку «а» по разным направлениям, получим:

1. Проходя через точку «а» в направлении осей координат, запишем:

; ;

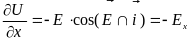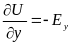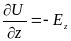
2. Проходя через точку «а» по линии l₁ перпендикулярно вектору напряжённости электрического поля (₁ = 90⁰) и вдоль него по линии l₂ (₂ = 0) (см. рис. 2-2), получим:

l₁ E l₂

a

Рисунок 2-2

;

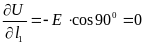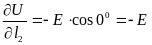
При перемещении перпендикулярно вектору напряжённости потенциал не изменяется, т. е. остаётся постоянным. Поэтому поверхности, перпендикулярные силовым линиям, называются равнопотенциальными (эквипотенциальными). Это направление обозначают через «a»

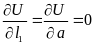
Направление вдоль линии напряжённости перпендикулярно поверхности равного потенциала. Часто это направление обозначают через «n», имея в виду нормаль к равнопотенциальной поверхности, тогда последнее соотношение можно записать иначе:

.

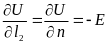Производная 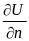ведёт себя как вектор, имеет составляющие, определяемые направляющими косинусами, и называется градиентом потенциала.

 grad U = – .

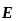Используя векторный оператор «набла», можем записать последнее выражение в декартовой системе координат:

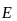– = grad U = = .

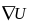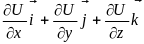Представление напряжённости через потенциал позволяет свести всю совокупность уравнений электростатики, записанных для векторов и 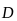, к одному дифференциальному уравнению, относительно потенциала. Разыскание скалярной функции – потенциала, является более лёгкой задачей , чем определение векторных характеристик поля. Поэтому нахождение потенциала является основной задачей электростатики. По найденному потенциалу U(x,y,z) легко определяется напряжённость электрического поля.