
- •Лекция 1
- •Закон полного тока и закон электромагнитной индукции в дифференциальной форме.
- •Полная система уравнений электромагнитного поля в дифференциальной форме.
- •Граничные условия
- •На поверхности раздела диэлектриков.
- •На поверхности раздела проводника и диэлектрика.
- •Теоремы Остроградского – Гаусса и Стокса.
- •Лекция 2 Электростатическое поле
- •Уравнения Пуассона и Лапласа.
- •Лекция 3
- •Применение функций комплексного переменного.
- •Метод заданного комплексного потенциала.
- •Лекция 4 Метод зеркальных изображений.
- •Метод конформных отображений.
- •Графический метод построения картины плоскопараллельного поля.
- •Электрическое поле в диэлектрике около проводников с постоянными токами.
- •Электрическое поле постоянных токов в проводящей среде.
- •Аналогия электрического поля постоянных токов и электростатического поля. Метод электростатической аналогии.
- •Расчёт сопротивления заземления
- •Моделирование электростатических полей полем постоянного тока в проводящей среде
- •Лекция 7
- •Плоскопараллельное магнитное поле.
- •Комплексный потенциал магнитного поля.
- •Магнитное поле двух нитей с прямым и обратным током.
- •Принцип соответствия плоскопараллельных электрических и магнитных полей.
- •Граничные условия в магнитном поле у поверхности ферромагнетиков.
- •Метод зеркальных изображений в магнитном поле.
- •Графический метод построения картины плоскопараллельного магнитного поля.
- •Приближенные методы расчёта и построения картины плоскопараллельного поля. Метод сеток.
- •Лекция 8 Векторный потенциал магнитного поля.
- •Случай линейных проводником с током.
- •Определение магнитного потока через векторный потенциал.
- •Расчёт индуктивностей.
- •Лекция 9 Индуктивность коаксиального кабеля.
- •Индуктивности тонких проводников с токами
- •Лекция 10 Метод участков.
- •Индуктивности систем параллельных проводов.
- •Взаимная индуктивность между двумя двухпроводными линиями.
- •Две двухпроводные линии, расположенные симметрично в параллельных плоскостях.
- •Линии расположены во взаимно перпендикулярных плоскостях.
- •Индуктивность трёхфазной линии.
- •Лекция 11 Переменное электромагнитное поле в диэлектрике
- •Вектор Умова-Пойнтинга.
- •Длина электромагнитной волны в диэлектрике.
- •Лекция 12 Переменное электромагнитное поле в проводящей среде.
- •Длина волны и затухание.
- •Понятие об электромагнитном экранировании.
- •Лекция 13
- •Активное сопротивление шины для переменного тока.
Приближенные методы расчёта и построения картины плоскопараллельного поля. Метод сеток.
В случае сложных границ области, в которой необходимо анализировать поле, можно применить один из приближенных методов, называемый методом сеток. Рассмотрим его применение на примере определения скалярного магнитного потенциала плоскопараллельного магнитного поля постоянных токов. Так как поле, описываемое скалярным магнитным потенциалом, существует только вне областей с токами, то во всех точках скалярный магнитный потенциал удовлетворяет уравнению Лапласа:
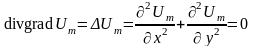 .
.
Разобьём исследуемую область с помощью линий, параллельных осям координат, на одинаковые ячейки, шириной x и высотой y (рис.7–7):
y

 y
y
b
a o c
d
x
x
Рисунок 7–7
Переходя к конечным приращениям, можем записать приближенное равенство:
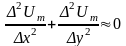 .
.
Рассмотрев произвольный узел сетки (o) и четыре примыкающие к нему узла (a,b,c,d), можем записать через приращения потенциалов и координат выражения для первых производных, а затем и вторую производную по оси абсцисс:
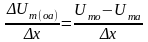
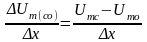
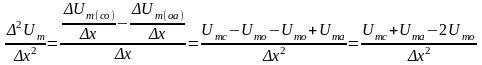
Аналогичное соотношение можно записать для второй производной от скалярного магнитного потенциала и по оси ординат:
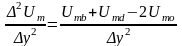 .
.
Подставляя обе вторые производные в уравнение Лапласа и принимая сетку квадратной (x = y), получаем:
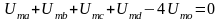 ,
откуда:
,
откуда: 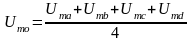 .
.
Полученное соотношение означает, что для квадратной сетки магнитный потенциал любого узла сетки может быть приближённо принят равным среднему арифметическому магнитных потенциалов соседних с ним узлов сетки.
Записав аналогичные уравнения для всех узлов сетки, и используя значения потенциала на границах области, можно вычислить потенциалы всех узлов, если решить совместно полученную систему уравнений.
Однако вместо совместного решения большого количества уравнений удобнее воспользоваться итерационным методом. Для этого необходимо задаться начальными приближениями потенциалов во всех узлах сетки, а затем, проверяя соотношения для потенциалов поочередно во всех узлах, уточнить потенциалы всех узловых точек. Полученные в результате первой итерации значения потенциалов узлов вновь проверяются и уточняются с помощью полученных соотношений. Проводя последовательно несколько итераций, удаётся получить значения потенциалов в узлах, которые сходятся к величинам, совпадающим с результатами непосредственного решением системы уравнений для узлов сетки.
Итерационный процесс сходится быстрее, если удаётся правильно задать начальные приближения для потенциалов узлов.
Лекция 8 Векторный потенциал магнитного поля.
В связи с тем, что введённый ранее скалярный магнитный потенциал Um позволяет описывать магнитные поля только в областях, не занятых электрическими токами, желательно ввести в рассмотрение какую-либо другую вспомогательную величину, с помощью которой можно было бы анализировать магнитные поля постоянных токов, как вне проводников с токами, так и внутри этих проводников. Это позволит анализировать поле в областях, где оно имеет либо потенциальный, либо вихревой характер.
Кроме того, желательно, чтобы эта новая вспомогательная величина была пригодна и для исследования переменных электромагнитных полей, т. е. для случая, когда плотность тока изменяется во времени (J(t) ≠ const).
Рассматривая уравнения магнитного поля:
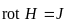 ;
;
;
;
;
;
мы видим, что второе уравнение будет выполняться всегда, если представить вектор магнитной индукции, как ротор некоторого вспомогательного вектора:
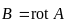 ; [
; [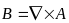 ];
]; 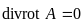 ; [
; [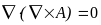 ].
].
Новый вектор
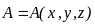 называют векторным потенциалом магнитного
поля. Он
является функцией координат, так как
зависит от распределения индукции в
пространстве, которая в свою очередь
зависит от распределения электрических
токов.
называют векторным потенциалом магнитного
поля. Он
является функцией координат, так как
зависит от распределения индукции в
пространстве, которая в свою очередь
зависит от распределения электрических
токов.
Наложим на векторный потенциал такие условия, чтобы при подстановке его в уравнения магнитного поля эти уравнения выполнялись бы во всех точках поля – как при
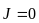 ,
так и при
,
так и при
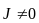 .
В этом случае векторным магнитным
потенциалом можно будет пользоваться
для анализа магнитных полей в любых
средах.
.
В этом случае векторным магнитным
потенциалом можно будет пользоваться
для анализа магнитных полей в любых
средах.
Принцип непрерывности магнитного потока выполняется всегда, так как именно на этом основании мы ввели векторный потенциал.
Подставляя векторный
потенциал в закон полного тока
,
и принимая, что магнитная проницаемость
среды не зависит от координат ( (x,y,z)
= const),
умножив обе части уравнения на ,
получим:
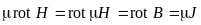 ,
что приводит к уравнению:
,
что приводит к уравнению:
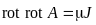 .
.
Рассмотрим последнее уравнение, используя векторный оператор Гамильтона (в декартовой системе координат). Преобразуем левую часть уравнения, применяя формулу для двойного векторного произведения:

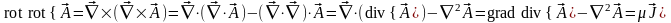 (*)
(*)
В полученном векторном уравнении скрыто три уравнения для проекций векторов на координатные оси. Вводя векторный потенциал, мы задали только одно уравнение для описания ротора этого вектора:
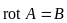 .
Для полного описания вектора необходимо
задать также его дивергенцию. При
рассмотрении магнитного
поля постоянных токов
примем, что дивергенция векторного
магнитного потенциала равна нулю:
.
Для полного описания вектора необходимо
задать также его дивергенцию. При
рассмотрении магнитного
поля постоянных токов
примем, что дивергенция векторного
магнитного потенциала равна нулю:
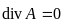 .
В интегральной форме это уравнение
записывается в виде:
.
В интегральной форме это уравнение
записывается в виде: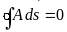 .
. Это
означает, что во всех точках магнитного
поля постоянного тока выполняется
принцип
непрерывности линий векторного
магнитного потенциала,
т. е. эти линии не имеют ни начала, ни
конца и являются замкнутыми на себя
кривыми. При рассмотрении граничных
условий в различных средах на основании
такого типа интегралов мы утверждали,
что на границе раздела сред остаются
неизменными нормальные по отношению
к границе составляющие соответствующего
вектора. В данном случае для векторного
магнитного потенциала можем записать:
Это
означает, что во всех точках магнитного
поля постоянного тока выполняется
принцип
непрерывности линий векторного
магнитного потенциала,
т. е. эти линии не имеют ни начала, ни
конца и являются замкнутыми на себя
кривыми. При рассмотрении граничных
условий в различных средах на основании
такого типа интегралов мы утверждали,
что на границе раздела сред остаются
неизменными нормальные по отношению
к границе составляющие соответствующего
вектора. В данном случае для векторного
магнитного потенциала можем записать:
A1n = A2n .
 Принятое
ограничение для дивергенции векторного
магнитного потенциала не сужает
возможностей применения уравнений
магнитного поля, так как вектор магнитной
индукции B
определяется лишь ротором векторного
потенциала и не зависит от его дивергенции.
Тогда из уравнения (*) получаем:
Принятое
ограничение для дивергенции векторного
магнитного потенциала не сужает
возможностей применения уравнений
магнитного поля, так как вектор магнитной
индукции B
определяется лишь ротором векторного
потенциала и не зависит от его дивергенции.
Тогда из уравнения (*) получаем: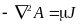 или
или
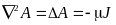
Так как в левой части уравнения стоит Лапласиан векторного потенциала, а правая часть уравнения не равна нулю, то полученное уравнение является уравнением Пуассона для векторного потенциала. В этом векторном уравнении содержится три уравнения для проекций векторов на оси координат, в частности для декартовой системы можем записать:
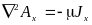 ;
; 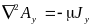 ;
; 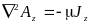 .
.Сопоставляя эти уравнения с уравнением Пуассона для скалярного электрического потенциала:
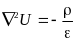 ,
,можем заметить, что одно уравнение переходит в другое при замене:
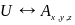 и
и 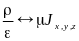
Решение уравнения Пуассона для скалярного электрического потенциала известно:
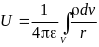
поэтому по аналогии можно записать решение уравнения Пуассона для проекций векторного потенциала:
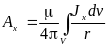 ;
; 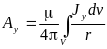 ;
; 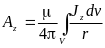 .
.Просуммировав умноженные на орты проекции векторного потенциала, получим решение уравнения Пуассона для векторного потенциала магнитного поля (под интегралом геометрическое суммирование):
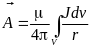
Интегрирование проводится по всей области (объёму), где плотность тока не равна нулю. Наиболее часто электрические токи, создающие магнитное поле, протекают по проводам, поэтому представляет интерес вычисление векторного магнитного потенциала для этого случая.
