Длина электромагнитной волны в диэлектрике.

Приращение координаты, на котором аргумент волны изменяется на 2, называется длиной волны (). Из соотношения =2 получим:

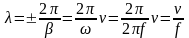. Либо иначе:

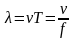
Так как скорость распространения электромагнитной волны в диэлектрике зависит только от его диэлектрических и магнитных свойств и не зависит от частоты передаваемого сигнала, то длина волны в диэлектрике обратно пропорциональна частоте сигнала. Длина электромагнитных волн в воздухе в зависимости от частоты (таблица 11–1) определяется из соотношения:

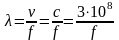
Таблица 11–1 Длина волны в воздухе для различных частот.

Частота	Длина волны	Диапазон	Примечание
f	
105 гц =100 кГц	3000 м	Длинные волны
106 гц =1 МГц	300 м	Средние волны
107 гц =10 МГц	30 м	Короткие волны
108 гц =100 МГц	3 м	УКВ; FM; компьютер	ТВ - метровый диапазон
109 гц =1000 МГц	0,3 м	Мобильная связь	ТВ - дециметровый диапазон

Лекция 12 Переменное электромагнитное поле в проводящей среде.

Рассмотрим закон полного тока и закон электромагнитной индукции:

;

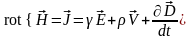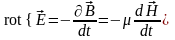
Токи переноса не могут существовать внутри проводящей среды, а токами смещения можно пренебречь по сравнению с токами проводимости. Тогда закон полного тока можно записать в виде:

.

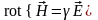Рассмотрим плоскую электромагнитную волну, распространяющуюся в диэлектрике и падающую перпендикулярно на поверхность проводящей среды. Направим ось z по направлению вектора скорости волны, т.е. внутрь проводника перпендикулярно его поверхности и запишем проекции уравнений на оси декартовой системы координат:

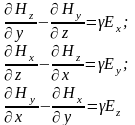
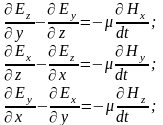
Учитывая, что волна плоская (все величины, характеризующие её, зависят только от координаты z), из записанной системы уравнений по аналогии с рассуждениями о плоской волне в диэлектрике, можем записать:

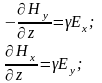
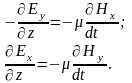
Направим ось y по вектору H. В этом случае H = H_y; H_x = 0 , поэтому E_y = 0, и уравнения упрощаются:

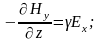
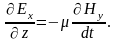
После дифференцирования первого уравнения по координате z и подстановке в него второго уравнения, получаем уравнение для вектора напряжённости магнитного поля и по аналогии запишем такое же уравнение для вектора напряжённости электрического поля:

; ; .

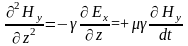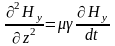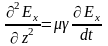Последние уравнения отличаются от волновых уравнений, полученных для этих векторов при рассмотрении переменного электромагнитного поля в диэлектрике тем, что содержат не вторую, а первую производную от векторов по времени.

Решение уравнения для установившегося синусоидального режима.

При рассмотрении установившегося синусоидального режима напряжённости электрического и магнитного поля можно записать в виде мгновенных значений и в комплексном виде:

;

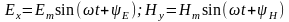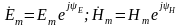
Так как в комплексном виде временная координата t исключается, а дифференцирование по времени заменяется умножением на jω , то переменные зависят только от одной пространственной координаты z, и уравнения могут быть записаны в полных производных:

; ;

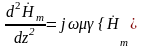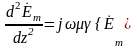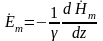
Решим уравнение для напряжённости магнитного поля:

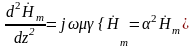, где ;

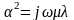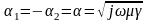– корни характеристического уравнения

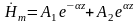
Преобразуем выражение для корня характеристического уравнения:

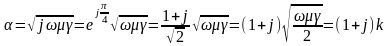, где

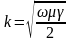
Тогда решение для напряжённости магнитного поля можно представить в виде:

.

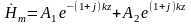При z, стремящемся к бесконечности, множитель e^kz и напряжённость магнитного поля также стремятся к бесконечности, что невозможно из физических соображений, поэтому: A₂ = 0

Окончательное выражение для напряжённости магнитного поля примет вид:

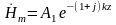
Постоянную A₁ определим из граничных условия на поверхности раздела проводника и диэлектрика (рис.12–1) при z = 0.

H_me H_m0

z

 

Рисунок 12–1

Так как волна распространяется по направлению, перпендикулярному к поверхности проводящей среды, то вектор напряжённости магнитного поля в диэлектрике H_me расположен параллельно границе и равен вектору напряжённости магнитного поля внутри проводящей среды вблизи её поверхности H_m0 (ввиду равенства на границе касательных составляющих). Поэтому, зная параметры волны у поверхности проводящей среды в диэлектрике, определяем постоянную A₁ из граничного условия: при z = 0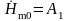

Окончательно можем записать: .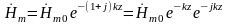

Полученное в комплексном виде решение представим в виде мгновенного значения:

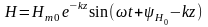
Запишем решение для комплексной амплитуды напряжённости электрического поля :

.

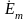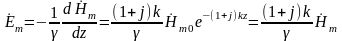Отношение комплексных амплитуд электрической и магнитной напряжённости определяет волновое комплексное сопротивление ( Z ) проводящей среды для синусоидальной электромагнитной волны:

.

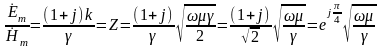Это сопротивление имеет вещественную и мнимую часть, что свидетельствует о наличии тепловых потерь в проводнике и сдвиге по фазе (  = + /4), между волнами электрической и магнитной напряжённости во временной области. Волновое сопротивление можно представить и в алгебраической форме:

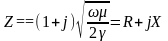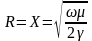, причем , а X - индуктивное сопротивление

Окончательное выражение для комплексной амплитуды напряжённости запишем в показательной форме:

.

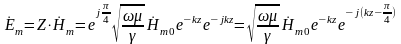Мгновенное значение напряжённости электрического поля имеет вид:

.

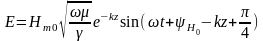Плотность тока проводимости определяется из соотношения J_пр = E и равна:

. (*)

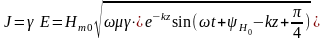Следует помнить, что в рассматриваемом случае плоской электромагнитной волны векторы напряжённости электрического и магнитного поля взаимно перпендикулярны в пространстве. Построим кривые, изображающие качественное распределение напряжённости электрического и магнитного поля вдоль оси z для некоторого момента времени (t = 0), принимая, что начальная фаза 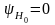(рис.12–2).

x

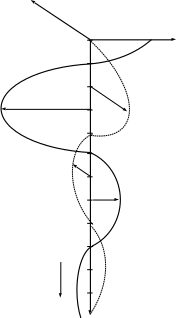
H_y

z

0

v

E_x

y

Рисунок 12–2

Волна напряжённости магнитного поля отстаёт по фазе от волны напряжённости электрического поля на 45 градусов. Амплитуды обеих волн по мере продвижения вдоль оси z вглубь проводника затухают со скоростью, определяемой множителем e^-kz.