Лекция 13

Неравномерное распределение синусоидального тока в плоском шинопроводе.

Рассмотрим систему из двух плоских проводящих шин высотой h и шириной d, расположенных параллельно и на достаточно малом расстоянии  друг от друга (рис. 14–1), причём l >> h >> d >> . В шинах протекает переменный синусоидальный ток – i.

y

l

x

i i

z

h 0

H_y H_y

E_x

S S

E_x

d 

Рисунок 14–1

Учитывая соотношения между размерами, считаем электромагнитную волну плоской, все её параметры зависят только от одной координаты z. Воспользуемся решением уравнений для плоской синусоидальной волны ( см. лекцию 12 стр. 2).

; ; ,

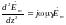где – корень характеристического уравнения

Для нахождения постоянных А₁ и А₂, используем граничные условия. Начало координат расположим на наружной поверхности левой шины, и определим значения напряжённости магнитного поля при z₁ = 0 и при z₂ = d. Рассматривая совокупность двух соседних шин с одинаковыми по величине и противоположными по направлению токами, применим закон полного тока.

Для контура l₁ , охватывающего обе шины с прямым и обратным током и расположенного вплотную к поверхностям обеих шин (рис.14–2а), получим:

.

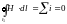Считаем, что снаружи, вне системы шин, магнитное поле отсутствует, т.е. при z₁ = 0

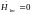, откуда А₁ + А₂ = 0, А₁ = – А₂ = А.

l₁ l₂

а) б)

Рисунок 14–2

Для контура l₂, охватывающего левую шину и расположенного вплотную к её поверхности (рис.14–2б), получим:

Пренебрегая составляющими по горизонтальным составляющим контура (d << h) и учитывая, что на левой границе (при z₁ = 0) H₁ = 0, получаем:

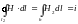, где H₂ – значение напряжённости при z₂ = d.

Так как волна плоская, то 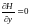, и во всех точках по высоте шины напряжённость магнитного поля (при z = const) одинакова. Это означает, что H₂ = const, и последний интеграл можно записать в виде:

H₂ h = i, или в комплексной форме: .

Отсюда определяем второе граничное условие: при z = d .

Подставляя найденное граничное условие в уравнение, получим:

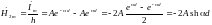
Теперь запишем выражение для постоянной A и для напряжённости магнитного поля в произвольной точке внутри левой шины:

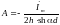
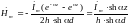
Используем полученное соотношение для анализа распределения тока по сечению шины. Определим плотность тока из закона полного тока:

; .

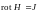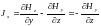Для комплексных значений можем записать:

; .

Анализировать распределение тока по сечению шины удобнее в безразмерном виде. С этой целью определим среднее по сечению шины значение плотности тока:

.

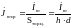Отношение плотности тока в произвольной точке сечения шины к средней плотности тока:

В полученном соотношении коэффициент  = (1 + j)k и гиперболические функции являются комплексными числами. Коэффициент, стоящий перед chz, – постоянное комплексное число. Отметим, что распределение тока по сечению шины не зависит от высоты шины h, но зависит от её толщины, так как электромагнитная волна затухает при распространении вдоль координаты z.

Запишем известные соотношения для гиперболических функций от суммы аргументов:

ch z = ch (1 + j)kz = ch kz·ch jkz + sh kz·sh jkz = ch kz·cos kz + j·sh kz·sin kz;

sh d = sh (1 + j)kd = sh kd·ch jkd + ch kd·sh jkd = sh kd·cos kd + j·ch kd·sin kd .

Эти соотношения необходимо использовать при расчёте конкретных значений относительной плотности тока в точке с координатой z.

Закон распределения тока по сечению шины зависит от удельного сопротивления материала шинопровода, его магнитной проницаемости и частоты переменного тока в шинопроводе. Все эти параметры входят в коэффициент k, который, как мы помним, равен:

.
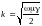