Индуктивности систем параллельных проводов.

В системе параллельных проводов с токами поле имеет плоскопараллельный характер, векторный потенциал, как и плотность тока, имеет единственную составляющую, направленную вдоль оси z.

В одной из предыдущих лекций мы рассматривали случай определения сцепленного с прямоугольной рамкой магнитного потока, созданного током в линейном проводе. Разность векторных магнитных потенциалов на разных сторонах рамки, удалённых на расстояния a и b от провода, мы получили в виде:

.

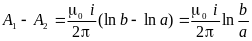По аналогии векторный магнитный потенциал в системе проводов с токами можем записать:

,

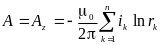где r_k – расстояние от рассматриваемой точки до соответствующего провода.

Для двухпроводной линии с прямым и обратным током (рис.10–4) определим внешнее потокосцепление и внешнюю индуктивность участка линии длиной l , используя контур, расположенный на ближних друг к другу поверхностях проводов.

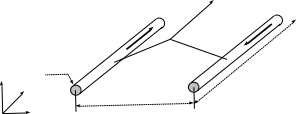A_z

1 2

i i

r₁ r₂

R l

z

D

Рисунок 10–4

В произвольной точке около двухпроводной линии векторный магнитный потенциал равен: .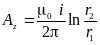

Тогда векторные потенциалы на внутренних поверхностях первого и второго провода имеют вид: ,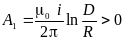

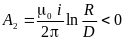а внешний магнитный поток и внешняя индуктивность двухпроводной линии равны соответственно:

;

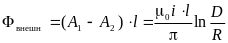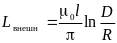
Внутренняя индуктивность этой линии определяется магнитным потоком внутри прямого и обратного провода (общая длина 2l ): .

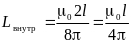Окончательно индуктивность двухпроводной линии равна: .

В реальных линиях расстояние между проводами превышает радиус провода примерно в 1000 раз, тогда: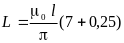

Взаимная индуктивность между двумя двухпроводными линиями.

Пусть первая линия с проводами 1 и 1^/ расположена параллельно второй линии с проводами 2 и 2^/ (рис. 10–5).

1 1^/

 ●

r₁₂ r₁₂^/ r₁^/₂^/

r₁^/₂

2 2^/

Рисунок 10–5

Зададимся током в первой линии и определим векторный магнитный потенциал на осях проводов второй линии:

; .

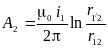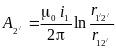Поток взаимоиндукции, сцепляющийся со второй линией, равен:

,

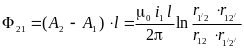а взаимная индуктивность между двумя двухпроводными линиями определяется соотношением:

.

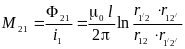Рассмотрим некоторые примеры при различном взаимном расположении линий.

Две двухпроводные линии, расположенные симметрично в параллельных плоскостях.

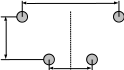
D₁

D₁

1 2 2^/ 1^/

1 1^/ D₂

б)

h

1 1^/

2 2^/

h

D₂ D

2 2^/

а) в)

Рисунок 10–6

В общем случае расстояние между проводами одной линии (D₁) и другой линии (D₂) различны (рис. 10–6а) при этом:

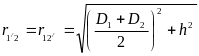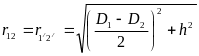; , поэтому:

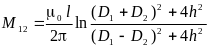
Если линии расположены на одной высоте (рис. 10–6б), то h = 0 и формула упрощается: .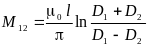

Если же расстояние между проводами линии (рис.10–6в) одно и тоже (D₁ =D₂ = D), то взаимная индуктивность определяется из выражения: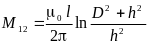

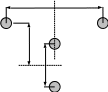
Линии расположены во взаимно перпендикулярных плоскостях.

1.Провода второй линии расположены в плоскости симметрии первой линии (рис. 10–7а). В этом случае: 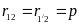, 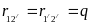при любых значениях D₁ , D₂ и b, поэтому: .

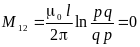При таком расположении две линии не оказывают влияния друг на друга через магнитное поле.

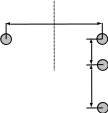D₁ D₁

1 1^| 1 1^|

b

b 2

2

D₂ D₂

2^| 2^|

а) б)

Рисунок 10–7

2. Провода второй линии расположены вне плоскости симметрии первой линии (рис. 10–7б). В этом случае:

; ;

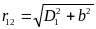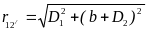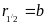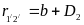; , поэтому:

.