
Динамика точки и системы / ДИНАМИКА
.pdf
3.31. Работа силы, приложенной к твердому телу при различных случаях его движения
Поступательное движение (элементарные перемещения точек тела одинаковы):
|
= Fdr |
(1) |
d A = Fvk dt = Fv dt |
||
A = M F dr |
|
(2) |
M 0 |
|
|
Вращательное движение вокруг неподвижной оси.
Скорость точки тела |
v = ω r |
(3) |
|
Элементарная работа
d A = F vdt = F (ω r ) dt |
(4) |
|
181 |
Момент силы |
mO |
(F ) = r F |
|
(5) |
|
|
|
||||
|
|
|
= mO (F) cos dt |
(6) |
|
d A = ω (r F) dt = ω mO (F) dt |
|||||
mО сos = моменту mz |
силы |
F |
относительно оси |
||
вращения Oz и dt = d , окончательно получаем |
|
||||
|
|
|
|
|
(7) |
|
d A = mzd |
|
|
||
Элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на дифференциал угла поворота тела.
182
Полная работа: |
|
|
|
A = |
|
mz d |
(8) |
|
|||
При mz = const : |
0 |
|
|
|
|
|
|
A = mz |
(9) |
||
где φ — угол поворота тела, на котором определяется работа.
Так как d φ = dt, и согласно формуле (7)
|
(10) |
d A = mO (F ) ω dt |
то мощность в случае вращения твердого тела вокруг неподвижной оси
|
|
|
|
|
N = |
d A |
= m |
ω = m |
(11) |
|
||||
|
dt |
O |
z |
183 |
|
|
|
|
Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равна произведению угловой скорости тела на момент силы относительно оси вращения.
Плоскопараллельное движение: |
|
|
|
|
v =vA + ω r |
(12) |
|||
где vA — скорость полюса А; |
|
|
|
|
r = AM. Тогда |
|
|||
d A = F v dt = F vA dt + F (ω r )dt. (13)
184
Далее, так как |
vAdt = drA ; |
|
|
|
|
F (ω r ) = ω (r F) = ω mA (F) = mzA |
(14) |
|
|
||
то |
|
(15) |
|
d A = F drA +mzAd |
|
где mzA — момент силы относительно оси, проходящей через полюс и перпендикулярной к плоскости движения.
Элементарная работа силы, приложенной к какой-либо точке твердого тела, в случае его плоскопараллельного движения равна сумме элементарных работ на
элементарном поступательном перемещении вместе с полюсом и элементарном вращательном перемещении
вокруг мгновенной оси, проходящей через полюс. |
185 |
|
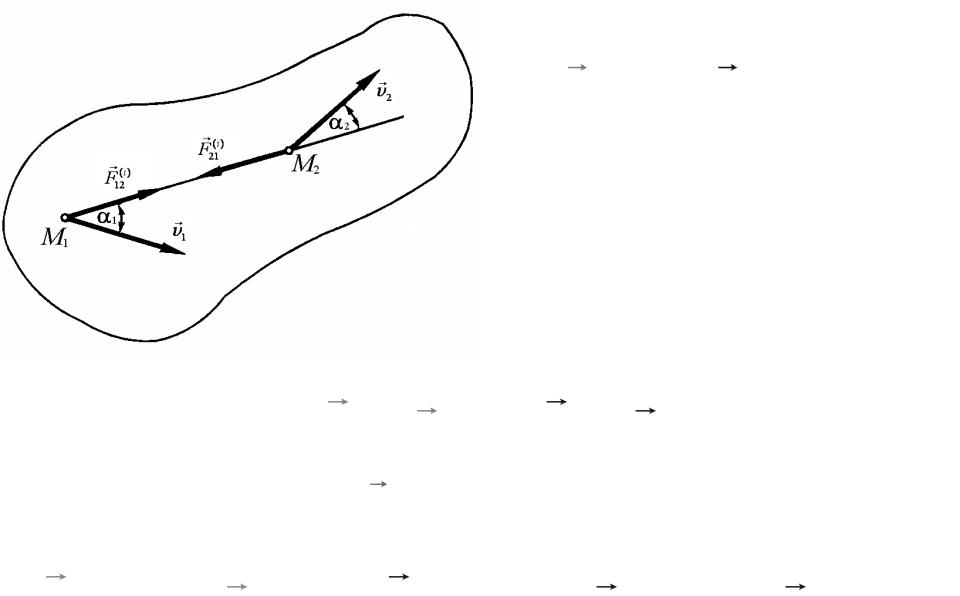
3.32. Работа внутренних сил, приложенных к твердому телу
F (i) = −F (i ) ; |
|
||
12 |
21 |
(1) |
|
F (i) = F (i) . |
|||
|
|||
12 |
21 |
|
|
Сумма элементарных работ внутренних сил рассматриваемых точек:
(i) |
(i) |
(i) |
(i) |
v2dt |
|
d A1 |
+ d A2 |
= F12 |
v1dt + F21 |
(2) |
e 0
Единичный вектор , направлен по направлению первой силы:
(i) |
(i) |
o |
; |
(i) |
(i) |
e |
o |
(i) |
e |
o |
186 |
F12 |
= F12 |
e |
F21 |
= −F21 |
|
= −F12 |
|
(3) |
Используем теперь формулы (3) для преобразования равенства (2)
d A1(i) + d A2(i) = F12(i) (v1 eo −v2 eo )dt =
(4)
= F12(i) (v1 cos 1 −v2 cos 2 )dt
0
Сумма элементарных, и следовательно, полных работ всех внутренних сил твердого тела равна нулю.
187
Лекция 7 3.33. Кинетическая энергия точки и механической системы
mv 2
Кинетическая энергия точки:
2
Кинетическая энергия системы материальных точек:
|
|
|
N |
m v 2 |
|
|
|
|||
|
|
T = |
k |
k |
|
|
(1) |
|||
|
|
|
|
|
|
|||||
|
|
k =1 |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
или |
N |
m v2 |
|
N |
m v |
v |
|
|
||
|
|
k |
|
|||||||
|
T = |
k k |
= |
|
|
k k |
|
188 |
||
|
k =1 |
2 |
|
k =1 |
2 |
|
|
(2) |
||
|
|
|
|
|
||||||
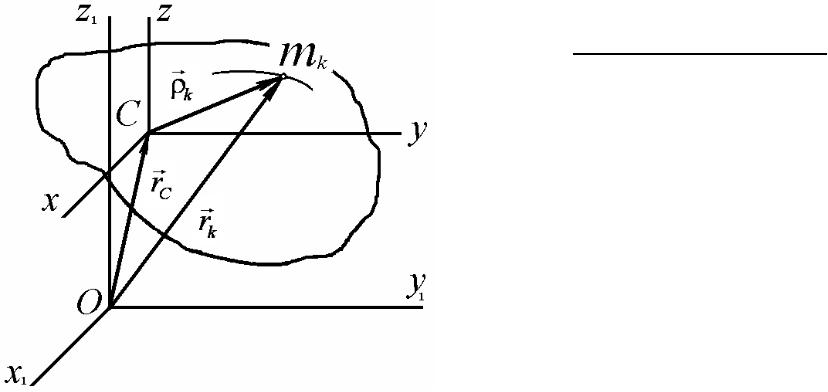
Теорема Кёнига
С – центр масс;
Ox1y1z1 - неподвижная система координат;
Сxyz - подвижная система координат с началом в центре масс С, Сxyz движется поступательно вместе с центром масс.
Абсолютное движение системы - совокупность переносного движения вместе с центром масс и относительного движения по отношению к центру масс
189
системы.
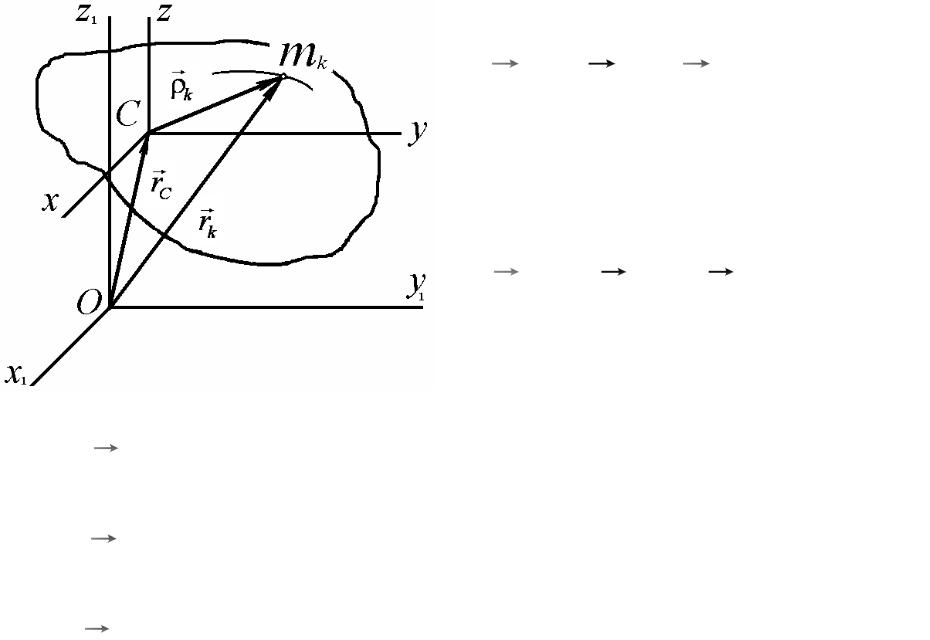
rk =rC + k |
(3) |
Дифференцируя получаем:
v |
k |
=v |
C |
+v(r ) |
(4) |
|
|
k |
|
где vk — абсолютная скорость k-й точки системы; vC — абсолютная скорость центра масс;
v(r)
k — относительная скорость k-й точки
190
относительно системы координат Сxyz.
