
Динамика точки и системы / ДИНАМИКА
.pdf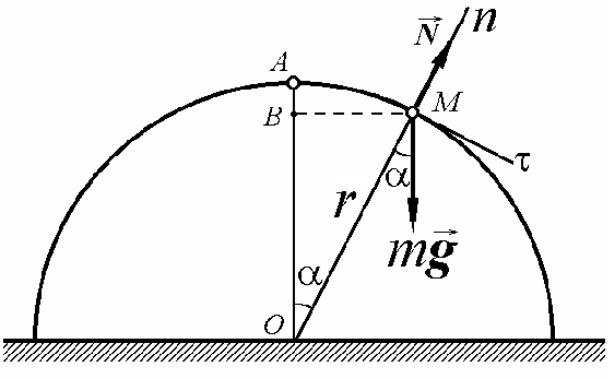
Пример 3.3. Материальная точка М вследствие малого толчка начинает движение из верхней точки А сферического купола, радиус которого равен r. Пренебрегая трением, определить, на какой высоте от плоскости основания нарушится контакт точки М с поверхностью купола. Чему равна скорость точки М в момент её отрыва от купола.
61
Решение. Уравнения движения точки в проекциях на естественные оси координат:
m |
dv |
|
= mg sin ; |
(1) |
dt |
|
|||
|
|
|
|
m |
v2 |
= mg cos – N. |
(2) |
|
|
r |
|||
|
|
|
|
|
Преобразуем (1)
dv |
|
v dv |
|
v dv |
(3) |
||
|
|
|
|
|
|
|
|
dt = |
|
ds |
= |
|
rd |
||
|
|
|
|||||
62
|
v dv |
= g sin |
|
|||
|
(4) |
|||||
|
rd |
|
|
|
||
|
|
|
|
|
||
Интегрируя (4) при v = 0 при = 0, получим |
|
|||||
v2 = 2gr (1 – cos ). |
|
|
|
(5) |
||
Из второго уравнения находим величину |
||||||
нормальной реакции |
v2 |
|
||||
|
|
|
|
|||
N = mg cos – m |
|
|
= mg (3cos –2). |
|
||
|
|
|
||||
N = 0, если cos 1 = 2/3.
r
Высота точки М над основанием при = 1 :
h = r cos 1 = 2r/3. |
(7) |
Скорость точки в момент отрыва v2 = 2gr/3. |
63 |
Лекция 3 3.9. Механическая система. Центр масс системы
Механической системой материальных точек -
совокупность взаимодействующих между собой материальных точек.
Неизменяемая - система, расстояние между точками которой при ее движении остается постоянным.
Абсолютно твердое тело представляет - пример неизменяемой системы.
64
Механическая система N материальных точек:
массы mk (k = 1, 2, …, N);
положение 3N координат (xk, yk, zk)
Масса системы:
|
N |
|
|
M = m1 + m2 +... + mN = |
|
mk |
(1) |
|
|||
|
|
|
k =1
65
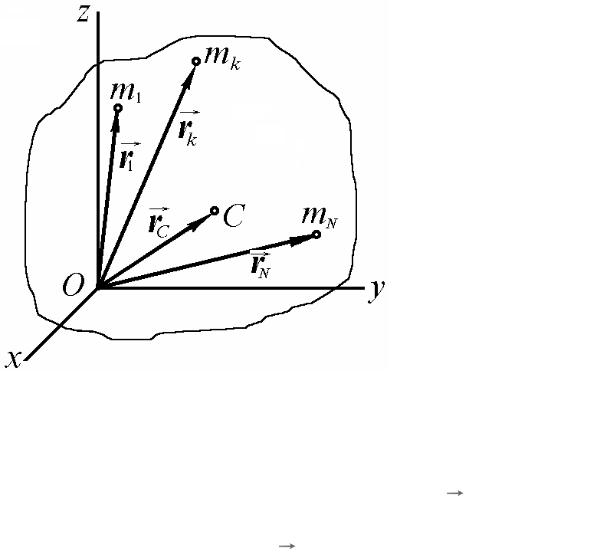
Центром масс механической системы - геометрическая точка C, положение которой определяется радиус-вектором:
|
|
N |
|
|
|
mk rk |
|
rC |
= |
k =1 |
(2) |
N |
|||
|
|
mk |
|
k =1
66
Координаты центра масс системы
|
N |
|
N |
|
N |
|
|
mk xk |
|
mk yk |
|
mk zk |
|
x = |
k =1 |
; y = |
k =1 |
; z = |
k =1 |
|
N |
N |
N |
||||
C |
C |
C |
||||
|
mk |
|
mk |
|
mk |
|
|
k =1 |
|
k =1 |
|
k =1 |
Статический момент массы системы:
N |
= MrC |
; |
|
mk rk |
(3) |
||
|
|
|
k =1
67
N
mk xk
k =1
N
mk yk
k =1
N
mk zk
k =1
=MxC ;
=MyC ;
=MzC .
Центр масс системы – это такая точка, относительно которой статический момент массы равен нулю.
68

3.10. Классификация сил, действующих на систему. Дифференциальные уравнения
движения системы
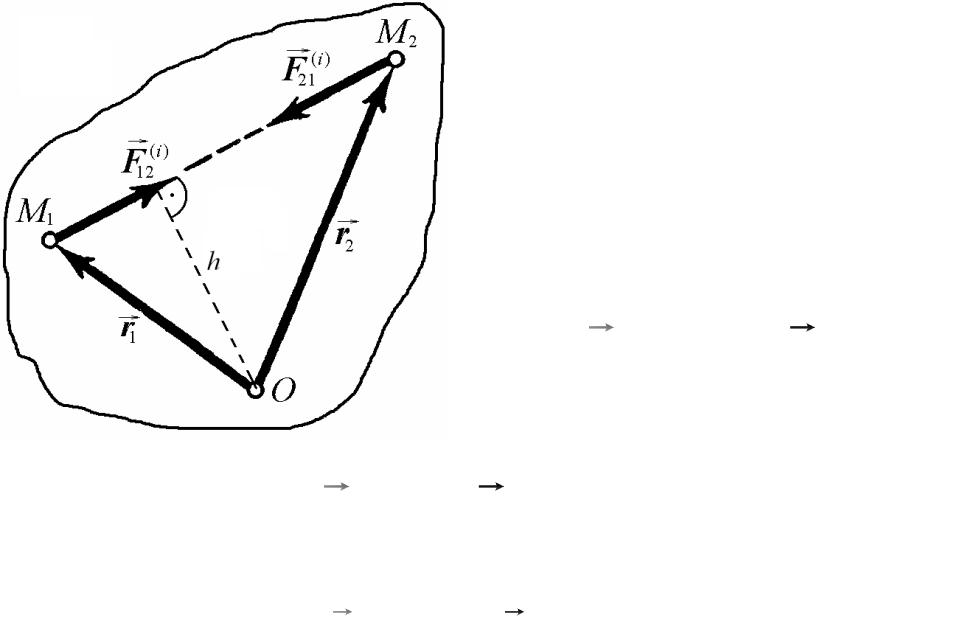
Внешние силы - силы взаимодействия между точками системы и точками, не принадлежащими к этой системе.
Внутренне силы - силы взаимодействия между точками системы.
Fk(e) - равнодействующая внешних сил
Fk( i ) - равнодействующая внутренних сил
69
Главный |
вектор |
всех |
внутренних |
|
сил |
механической системы равен нулю.
F12(i ) = −F21(i )
|
(i ) |
(i ) |
= 0 |
|
F12 |
+ F21 |
(1) |
||
|
|
|
|
|
R |
|
N |
= 0 |
|
|
= Fk |
|
||
|
(i) |
(i) |
|
(2) |
|
|
|
|
|
k =1 |
70 |
|
