1490

связи с этим, при решении практических задач необходимо оценить полосу частот исследуемого сигнала, в которой сосредоточена основная часть энергии сигнала. Под основной частью энергии понимают обычно величину не менее чем 0.9 полной мощности сигнала, а полосу частот, в которой сосредоточено 90% мощности сигнала, называют эффективной шириной спектра сигнала.

Определим эффективную ширину спектра для трех типов сигнала, рассмотренных в п. 2.3, а именно: прямоугольный импульс, экспоненциальный импульс и функция Гаусса [11, 12].

2.4.1. Эффективная ширина спектра прямоугольного импульса

Напомним прежде всего, что при анализе спектральной плотности прямоугольного импульса, определенной выражением (2.10а)

ω =τ sinωτ 2 x( )

ωτ 2

было рассмотрено соотношение между длительностью импульса τ и полушириной главного лепестка его спектральной плотности. При этом полушириной главного лепестка был назван интервал угловых частот 0 <ω ≤ 2π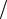τ . Представляется чрезвычайно интересным определить часть энергии прямоугольного импульса, содержащейся в данной полосе частот, поскольку именно для этой полосы частот был установлен принцип неопределенности, характеризуемый выражением ∆f ∆τ =1. Учитывая, что амплитуда импульса была принята единичной, нетрудно установить, что полная энергия P прямоугольного импульса длительностью τ определяется площадью импульса, т.к.

62

τ 2

P = ∫ 12dt =τ.

−τ 2

Поскольку, в соответствии с теоремой Парсеваля, полная энергия определяется как

а для симметричного энергетического спектра это выражение может быть записано в виде

63

Интеграл, входящий в выражение (2.17), после интегрирования по час-

где z =ωВτ . Функция (2.19) представляет собой одну из форм интеграль-

ного синуса и подробно табулирована (см. например таблицы А. Анго [3] ). Используя (2.19), перепишем выражение (2.18), определяющее часть энергии, заключенную в полосе [0,ωВ] , в окончательном виде

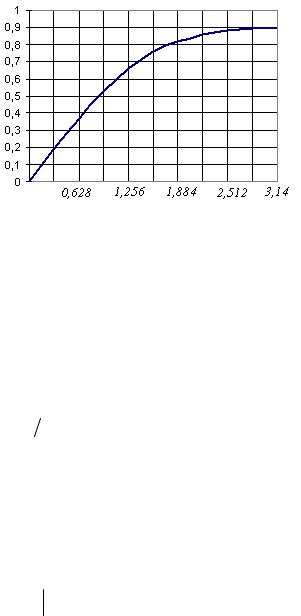
ωВτ2 , дает результат, представленный на рис 2.9. Из этого рисунка вид-

фильтра при достаточно эффективном использовании энергии импульса. Однако в случае, если требуется получить на выходе фильтра форму им-

64

пульса, близкую к прямоугольной, полоса пропускания фильтра должна быть значительно шире.

Рис. 2.9. К определению эффективной ширины спектра

2.4.2. Эффективная ширина спектра экспоненциального импульса

Соответственно, энергетический спектр экспоненциального импульса определяется как

Определим теперь эффективную ширину спектра (2.21), т.е. полосу частотой [ω, ωВ ], в которой сосредоточенно 90% энергии импульса. Для определения эффективной ширины спектра воспользуемся соотношением

Тогда

65

Подставляя пределы интегрирования, получим arctg ωαВ = 0,45π ,

откуда верхняя частота эффективной ширины спектра определяется, как

ωВ = tg(0,45π)α = 6,28/τ .

Учитывая, что ωВ = 2π fВ , нетрудно увидеть, что верхняя частота эф-

фективной ширины спектра экспоненциального есть

fВ = ωπВ =τ1

2

Таким образом, 90% энергии экспоненциального импульса сосредоточено в полосе частот от 0 до fВ =1τ . Данный результат совпадает с опре-

делением эффективной полосы частот прямоугольного импульса (см. под-

раздел 2.4.1).

2.4.3. Эффективная ширина спектра гауссова импульса

Спектральная плотность гауссова импульса x(t) = exp(−t2 2τ2 ) опреде-

лена выражением (2.14)

X (ω) = 2πexp −ω2τ2 .

2

Полная энергия гауссова импульса может быть найдена в виде

Используя замену переменных t /τ = x , dt = dxτ , преобразующую выражение (2.24) в интеграл Эйлера – Пуассона, определим полную энергию импульса как

66

Найдем теперь эффективную ширину спектра гауссова импульса, в пределах которой сосредоточено 90% энергии импульса. Для этого проинтегрируем энергетический спектр гауссова импульса

X& (ω) 2 = 2πτ2exp(−ω2τ2 )

от нуля до некоторой частоты ωВ , и найдем эту частоту, исходя из условия

90 – процентного содержания энергии импульса в полосе [0, ωВ]

Определим энергию гауссова импульса в полосе [0, ωВ] как

который табулирован во многих справочниках, например [13].

Для преобразования выражения (2.26) используем замену переменных ωτ = r , dω = dr / dτ и перепишем это выражение как

Из выражения (2.28) следует, что отношение энергии P∆ω , заключенной в полосе частот [0, ωВ], к полной энергии гауссова импульса P равно

Для 90 – процентного содержания энергии импульса в полосе [0, ωВ]

левая часть выражения (2.29) равна 0.9, что и позволяет, используя таблицы интеграла вероятностей, определить величину аргумента Z =ωВτ ≈1,16.

67

Учитывая, что τ представляет собой половину длительности гауссова импульса на уровне, 1/ e ≈ 0,606 т.е. τ = 0,5∆t , видим, что π fВ∆t =1,16

откуда верхняя частота эффективной полосы спектра может быть получена

ввиде fв ≈ 037 / ∆t .

2.5.Основные свойства преобразования Фурье

(теоремы о спектрах)

Рассмотрим несколько общих теорем о спектрах, основанных на свойствах преобразования Фурье [1, 3, 7, 8, 11].

2.5.1. Теорема сложения (теорема линейности)

Отметим прежде всего, что преобразование Фурье линейно. Отсюда следует, что к нему применим принцип суперпозиции и это обстоятельство можно сформулировать следующим образом:

Преобразование Фурье взвешенной суммы (разности) сигналов равно взвешенной сумме (разности) спектров этих сигналов:

Здесь fi (t) и Si (ω) есть функции времени и отвечающие им спектры, а ai

есть некоторые весовые коэффициенты.

Сложение комплексных спектральных плотностей производится по правилам сложения комплексных чисел

Спектр амплитуд и спектр фаз суммы спектров определяется как

68

2.5.2. Теорема смещения (теорема задержки)

Рассмотрим влияние временного смещения (задержки) сигнала на его спектр. Анализ проведем с использованием конкретного примера.

Пусть имеют место два сигнала в виде прямоугольных импульсов длительностью τ , обладающих единичной амплитудой. Однако их расположение на оси времени различаются: один из сигналов расположен симметрично относительно начала координат, а второй смещен относительно первого на величину τ / 2 (см. рис 2.10, а, б).

x(t )

Рис. 2.10а. Прямоугольный импульс x(t )

Рис. 2.10б. Смещенный прямоугольный импульс

69

Спектр несмещенного сигнала определяется выражением (2.10а)

Модуль X& (ω) и фаза ϕ(ω) этого спектра изображены на рис 2.11, а, б.

Рис. 2.11а

ϕ(ω)

π

ω

−π

Рис. 2.11б

ϕ(ω)

ω

Рис. 2.11в

Рис. 2.11. Амплитудный и фазовый спектры смещенной функции

70

Рассмотрим теперь выражение для комплексного спектра сигнала, отличающегося от первоначального сигнала произвольным смещением (запаздыванием) на время ∆t

Используя замену переменных t − ∆t =t1 , t =t1 + ∆t , dt = dt1 , перепишем

(2.31) в виде

X&1(ω) = ∞∫ x(t1)exp[− jω(t1 + ∆t)]dt1 =

−∞

= exp(− jω∆t ) ∞∫ x(t1)exp(− jωt1 )dt = X& (ω)exp(− jω∆t ), (2.32)

−∞

где X& (ω) есть спектр несмещенной функции. Таким образом, теорема о спектре смещенной функции может быть сформулировать следующим образом:

Если функция x(t) , обладающая спектральной плотностью X& (ω) ,

смещена на время ∆t , то спектр смещенной функции определяется произ-

ведением спектра несмещенной функции X& (ω) и фазового множителя exp(− jω∆t) :

X&1(ω) = X& (ω)exp(− jω∆t) . (2.33)

Для конкретного примера смещенного прямоугольного импульса (см. рис. 2.10, б), получим:

X&1(ω) = ∫τ0 exp(− jωt )dt =− j1ω exp(− jωt )τ0 =

= − j1ω exp(− jωt )−1 = j1ω[1−cosωτ + j sinωτ].

Используя выражения sin2 α2 = 0,5(1−cosα) , sin 2α = 2cosαsinα пре-

образуем последнее соотношение к виду

71