1490

В состав основной тригонометрической системы входят как четные функ-

ции (1, cos 2πT k t , …), так и нечетные функции (sin 2Tπ t , …, sin 2πT k t ).

Если функция ξ (t ), заданная на интервале [−T / 2; T / 2], четная, то ее

разложение в ряд Фурье имеет вид

22

1.4. Ряд Фурье в комплексной форме. Спектр периодической функции

Перепишем для удобства выражение (1.11) для тригонометрического ряда Фурье

23

Рассматривая соотношения (1.29а, б) можно сделать следующие выводы:

1. Выражение 0,5(ak + jbk ) может быть получено из выражения

0,5(ak − jbk ) при изменении знака индекса k : k → −k . Тогда, если ввести обозначение

в случае k = 0 . Следовательно, выражение (1.28) можно переписать в виде

24

Соотношение (1.31) есть разложение периодической функции ξ (t ) в

ряд Фурье, обладающий комплексными коэффициентами C&k , которые оп-

ределяются выражением (1.30), или, иначе, рядом Фурье в комплексной форме. Этот ряд является более простым по структуре и имеет то преимущество, что все коэффициенты разложения определяются единственной формулой (1.30). Рассматривая физический смысл ряда (1.31), нетрудно видеть, что в разложении присутствуют как положительные гармоники с индексом k , так и отрицательные с индексом −k . Хотя отрицательные частоты физически не существуют, их использование создает определенные удобства для анализа, поскольку операции с комплексными числами значительно проще. Нетрудно видеть также, что ряд Фурье в действительной форме может быть получен путем отбрасывания гармоник с отрицательными частотами и удвоения амплитуд гармоник с положительными частотами (для значений k ≥1).

Относительно определения значений коэффициентов C&k для случая k < 0 (т.е. для отрицательных частот) нетрудно показать, что для действи-

тельных функций ξ (t ) справедливо следующее: поскольку для положи-

тельных значений k

то для отрицательных величин (−k )

Таким образом, для действительных функций времени комплексные коэффициенты Фурье (комплексные амплитуды) гармоник с отрицательной

25

частотой определяются комплексно-сопряженными коэффициентами Фурье соответствующих гармоник с положительной частотой.

Сопоставляя амплитудно-фазовую форму ряда Фурье (1.10б), его тригонометрическую (1.11) и комплексную (1.31) формы, нетрудно видеть,

плексным спектром этой функции [1, 7]. Набор модулей комплексных ам-

плитуд C&k , характеризующий частотную зависимость амплитуд гармоник называется амплитудным спектром функции ξ (t ). Набор величин ϕk , ха-

рактеризующий зависимость начальной фазы гармоник от частоты, назы-

вается фазовым спектром, а набор величин Pk =C&kC&k = C&k 2 , характери-

зующий частотное распределение мощности гармоник называется спектром мощности.

Комплексный спектр функции можно наглядно представить графиче-

ски. Если расположить векторные амплитуды C&k гармонических состав-

26

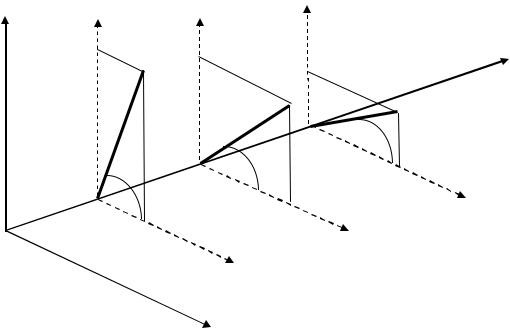
ляющих разложения в трехмерном пространстве, совместив действитель-

ную часть ReC&k с осью OX (при этом мнимая часть ImC&k будет автома-

тически совмещена с осью OY ), а номера гармоник расположить вдоль оси OZ , то будет получено трехмерное разложение действительной функции

ξ (t ) в комплексный ряд Фурье (см. рис. 1.1).

ReC&k

Рис. 1.1. Графическое представление комплексного спектра

1.5. Примеры разложения периодических функций в ряд Фурье. Некоторые свойства спектра периодических функций

Рассмотрим ряд примеров разложения периодических функций в ряд Фурье и продемонстрируем на этих примерах некоторые свойства спектра.

1.5.1. Разложение в ряд Фурье периодической последовательности прямоугольных импульсов

Зададим периодическую последовательность прямоугольных импульсов, следующих с периодом T и имеющих длительность τ (рис. 1.2). Для упрощения расчетов амплитуду импульсов примем за единицу. Считая, что

27

один из импульсов последовательности расположен симметрично относительно начала координат (см. рис. 1.2.), представим данную последовательность комплексным рядом Фурье (1.31) и определим коэффициенты разложения

ξ (t )

τ

T

Рис. 1.2. Периодическая последовательность прямоугольных импульсов

Величина q =T /τ называется скважностью. Набор коэффициентов C&k

представляет собой комплексный спектр импульсной последовательности,

характеризует распределение амплитуд и фаз частотного (спектрального) представления анализируемого сигнала. Амплитуды спектральных (гармонических) составляющих могут быть изображены в виде так называемых «спектральных линий», расположенных вдоль оси частот, а изменение

28

огибающей комплексной амплитуды спектральных коэффициентов определяется функцией (1.35), известной в математике как первый замечательный предел. Значение этого предела в точке k = 0 есть единица. Таким образом, спектр периодической функции является дискретной функцией частоты.

Рис. 1.3. Спектр периодической последовательности прямоугольных импульсов

Для определения спектра последовательности, изображенной на рис. 1.2. была использована комплексная форма ряда Фурье, но нетрудно показать, что, с учетом четности анализируемой функции, коэффициенты представления этой функции тригонометрическим рядом Фурье имеют вид

Таким образом, использование комплексной формы ряда Фурье предпочтительнее, поскольку сокращает объем вычислений.

Отметим, также, что функция (1.36) является знакопеременной и не может быть спектром амплитуд, который представляет собой набор модулей коэффициентов C&k ≥ 0 . Поскольку отрицательные лепестки спектра ха-

29

рактеризуются отрицательными величинами C&k , эти величины можно за-

писать в виде (−1) C&k = C&k exp{jπ}. Таким образом при переходе функции sin x / x в отрицательную область фазы спектральных линий, входящих в состав отрицательного лепестка спектра, претерпевают скачок на 1800 относительно фаз спектральных линий положительных лепестков. На рис. 1.4 изображены спектры амплитуд и фаз периодической последовательности прямоугольных импульсов.

C&k

1

π

0

Рис.1.4. Амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов

Продолжим анализ спектрального разложения (1.34) с целью установления связи между шириной основного лепестка спектральной функции и длительностью одиночного импульса последовательности. За основной лепесток примем часть графика функции шириной ∆f , заключенную меж-

полуширина основного лепестка (т.е. расстояние от начала координат до первого нуля) определяется из условия

30

спектра (основному лепестку). Назовем величину ∆f шириной основного

из которой следует, что произведение длительности импульса на ширину главного лепестка его спектра есть постоянная величина.

Выражение (1.38) есть одна из форм принципа неопределенности, из которого следует, что ширина спектра и длительность импульса обратно пропорциональны.

В дальнейшем будет показано, что в основном лепестке спектра сосредоточено более 90% энергии сигнала и поэтому в большинстве случаев ширину основного лепестка называют шириной спектра сигнала.

1.5.2. Теорема смещения для разложения в ряд Фурье

Рассмотрим разложение в ряд Фурье последовательности прямоугольных импульсов с единичной амплитудой, длительностью τ и периодом T (рис. 1.5). Начало первого импульса последовательности в данном случае совпадает с началом координат, т.е. данная последовательность смещена во времени на величину τ / 2 относительно последовательности ξ (t ), изо-

31