
1490
.pdf
Рис. 3.9. Формирование сигнала на выходе НЧ – фильтра при поступлении на вход фильтра прямоугольного импульса
3.5.3. Прохождение функции единичного скачка через фильтр высоких частот
Рассмотрим процесс передачи функции единичного скачка
1 при t > 0, x(t) =
0 при t < 0,
обладающей преобразованием Лапласа X (s) =1/ s , через фильтр высоких частот, характеризуемой передаточной функцией
H&ВЧ(s) = (1 +sτs0τ0 ) .
Преобразуем, прежде всего, передаточную функцию фильтра высоких частот к виду
122
H&ВЧ |
(s) = |
sτ0 +1 −1 |
=1− |
1 |
|
, |
(3.45) |
|
τ0 (s +1/τ |
0 ) |
|||||
|
|
1 + sτ0 |
|
|
|||
а затем найдём преобразование Лапласа выходного сигнала ВЧ фильтра в виде:
Y (s) = H&ВЧ(s) X (s) = |
1 − |
1 |
|
. |
(3.46) |
|
τ0 (s +1/τ |
0 )s |
|||||
|
s |
|
|
Для определения формы зависимости выходного сигнала от времени,
произведем обратное преобразование Лапласа над |
|
выражением (3.46): |
||||||||
(−1) |
(−1) |
1 |
|
(−1) |
|
1 |
|
|
|
|
L |
[Y (s)]= L |
|
|
− L |
|
|
|
|
. |
(4.47) |
|
(s +1/τ0 )s |
|||||||||
|
|
s |
|
|
τ0 |
|
|
|||
Обратное преобразование Лапласа первого слагаемого в выражении (3.47)
есть |
не что иное, как функция единичного скачка ( y(t) =1 |
при t > 0 , |
y(t) = 0 при t < 0 ) поскольку единственный полюс функции 1/ s |
равен ну- |
|
лю, |
а отвечающий ему вычет равен единице. Обратное преобразование |
|
Лапласа второго слагаемого найдено в подразделе 3.5.1 и определяется выражением (3.44). Тогда форма временного сигнала на выходе ВЧ – фильтра при подаче на его вход функции единичного скачка определяется как
y(t) =1 −1 +exp(−t /τ0 )= exp(−t /τ0 ), t > 0 . |
(3.48а) |
Выходной сигнал (3.48а) изображен на рис. 3.10.
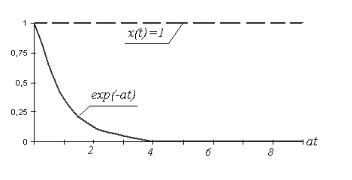
Рис. 3.10. Прохождение функции единичного скачка через фильтр высоких частот
123

Из данного рисунка следует, что функция единичного скачка после прохождения ВЧ – фильтра превращается в узкий импульс, длительность которого определяется постоянной времени фильтра. Плоская вершина единичного скачка, определяемая составляющими нижних частот, исчезает, поскольку ВЧ – фильтр подавляет нижние частоты входного сигнала. Процесс обострения выходного сигнала фильтра по сравнению со входным сигналом есть не что иное, как процесс дифференцирования входного сигнала и поэтому фильтры высоких частот называются дифференцирующими цепями.
3.5.4. Прохождение прямоугольного импульса через фильтр высоких частот
В заключение подраздела 3.5 рассмотрим процесс прохождения прямоугольного импульса с единичной амплитудой
1 при 0 <t <τ, x(t) =
0 при всех других значениях t
через фильтр высоких частот, передаточная функция H2 (s) которого оп-
ределяется выражением (3.45)
H&ВЧ(s) =1 −τ0 (s +11/τ0 ) .
Учитывая, что преобразование Лапласа входного сигнала имеет вид
X (s) = 1 − exp(−sτ ), s s
запишем преобразование Лапласа Y (s) выходного сигнала ВЧ – фильтра в виде
124
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
exp |
( |
−sτ |
) |
|
||||
Y (s) = H& |
ВЧ (s) X (s) = 1 − |
|
|
|
|
|
1 − |
|
|
|
= |
|||||||||||
τ0 (s +1/τ |
|
|
|
s |
|
|||||||||||||||||
|
|
|
|
|
|
0 ) s |
|
|
|
|
||||||||||||
|
|
1 |
|
|
exp |
( |
−sτ |
) |
|
|
exp |
( |
−sτ |
) |
|
|
|
|
|
|||
= 1 − |
|
|
|
− |
|
|
− |
|
|
|
|
|
=Y1(s) −Y2 (s) . |
|||||||||
sτ0 (s +1/τ |
|
|
|
s |
|
|
|
|
|
|
|
|||||||||||
s |
0 ) |
|
|
|
sτ0 (s +1/τ0 ) |
|
|
|
|
|||||||||||||
Функция времени |
y(t) |
на выходе ФЧ – фильтра определяется обратным |
||||||||||||||||||||
преобразованием Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L(−1) [Y (s)]= L(−1) [Y1(s)]− L(−1) [Y2 (s)]= y1(t) − y2 (t), |
|||||||||||||||||||||
где функции y1 (t) и y2 (t) определены |
|
на интервалах времени t > 0 и t >τ |
||||||||||||||||||||
соответственно. Слагаемое |
y1 (t) определяется выражением (3.48): |
|||||||||||||||||||||
y1(t) = exp(−t /τ0 ) , t > 0 ,
а для слагаемого y2 (t) запишем обратное преобразование Лапласа |
|
||||||||||||
−1 |
exp(−sτ) |
|
exp(−sτ) |
−1 |
exp(−sτ) |
−1 |
exp(−sτ) |
|
|||||
y2 (t) = L |
|
s |
− |
|
|
= L |
|
s |
|
− L |
|
|
. |
|
|
||||||||||||
|
|
|
sτ0 (s +1/τ0 ) |
|
|
|
|
sτ0 (s +1/τ0 ) |
|||||
Первое слагаемое последнего соотношения даёт функцию единичного скачка, смещённую на время τ , а для определения второго слагаемого воспользуемся разложением Хевисайда, вычеты в котором определяются как
k1 =1, k2 = −exp(−sτ) .
Тогда y2 (t) для t >τ определяется выражением
y2 |
|
−t −τ |
|
|
−t −τ |
|
(t) =1 −1 +exp |
|
= exp |
. |
|||
|
|
τ0 |
|
|
τ0 |
|
Таким образом, выходной эффект будет иметь вид:
y(t) = y1 (t) − y2 |
(t) = exp(−t /τ |
|
−t −τ |
|
, |
(3.48б) |
0 ) −exp |
|
|||||
|
|
|
τ0 |
|
|
|
где функции y1 (t) и y2 (t) определены на интервалах t > 0 и t >τ |
соответ- |
|||||
ственно. |
|
|
|
|
|
|
125

Графически выходной сигнал изображён на рис. 3.11
Рис. 3.11. Прохождение прямоугольного импульса через фильтр высоких частот
Из рис. 3.11 следует, что после прохождения дифференцирующей цепи плоская вершина исчезает, а переднему и заднему фронтам отвечают узкие положительный и отрицательный импульсы, длительность которых определяется постоянной временной цепи.
3.6.Применение интеграла свертки для анализа линейных систем
Внастоящем подразделе рассмотрен метод определения выходного сигнала линейной системы с использованием интеграла сверти и его связь с методом анализа систем в частотной области.
3.6.1.Преобразование Лапласа свертки
Как было показано выше, методы спектрального анализа, использующие преобразования Фурье и преобразования Лапласа, тесно связаны. Однако ценность преобразования Лапласа заключается в снятии ограничений,
126
связанных с проблемой интегрируемости анализируемых функций и об этом не следует забывать даже в случае, когда рассматриваются свойства преобразований Лапласа, идентичные свойствам преобразований Фурье.
Рассмотрим интеграл свертки [1, 2, 8, 16]
|
y(t )= ∫t |
x(τ )h(t −τ )dτ , |
(3.49) |
|
0 |
|
|
в котором функция x(t ) |
представляет собой сигнал на входе линейной |
||
системы (цепи), функция |
y (t ) есть сигнал на выходе этой системы, а |
||
функция h(t ) является характеристикой системы во временной области и называется импульсной реакцией ( или реакцией на единичный импульс). Ниже эта функция будет рассмотрена подробно.
Нашей задачей является доказательство того факта, что интеграл свертки (3.49) является во временной области эквивалентом обратного преобразования Лапласа выражения (3.41)
Y (s)= H& (s)X (s)
которое использовалось при анализе линейных систем (цепей) в частотной области. Здесь, как и ранее, Y (s) – преобразование Лапласа выходного сигнала. X (s)– преобразование Лапласа входного сигнала, а H (s) – пе-
редаточная функция.
Найдем преобразование Лапласа выражения (3.49):
∞ |
∞ t |
|
∫y(t )exp(−st )dt = ∫ ∫x(τ )h(t −τ )dτ |
||
0 |
0 0 |
|
= ∞∫ ∞∫x(τ )h(t −τ )dτ exp(−st ) |
||
0 0 |
|
|
exp(−st )dt =
dt. (3.50)
Учитывая, что интеграл в левой части равенства (3.50) есть преобразование Лапласа выходного сигнала и меняя порядок интегрирования, получим
127
Y (s)= ∞∫x(τ ) |
∞∫h(t −τ )exp(−st )dt dτ . |
(3.51) |
||
0 |
|
0 |
|
|
В выражении (3.51) внутренний интеграл представляет собой преобразова-
ние Лапласа смещенной функции h(t )
∞∫h(t −τ )exp(−sτ )dt = H& (s)exp(−sτ ).
0
Подставляя этот результат в (3.51), видим что
Y (s)= H& (s)∞∫x(τ )exp(−sτ )dτ = H& (s)X (s). |
(3.52) |
0 |
|
Таким образом, преобразование Лапласа свертки определяется как произведение преобразований Лапласа свертываемых функций. В силу взаимной однозначности прямого и обратного преобразований Лапласа очевидно, что результат (3.52) после применения к нему обратного преобразования Лапласа приведет к выражению (3.49).
3.6.2.Импульсная реакция линейной цепи
Впредыдущем подразделе было показано, что преобразование Лапласа функции h(t ), называемой импульсной реакцией цепи, дает передаточную
функцию цепи H& (s), т.е.
H& (s)= ∞∫h(t )exp(−st )dt.
0
Импульсной реакцией линейной цепи называется ее отклик на входное воздействие в виде единичного импульса, т.е. функции δ (t ). Свойства этой функции были рассмотрены в главе 2. В частности, было указано, что эта функция обладает так называемым фильтрующим свойством
128
∞∫x(t )δ (t −t0 )dt = x(t0 ).
0
Преобразование Фурье δ – функции также было рассмотрено в главе 2, но в данной главе необходимо использовать ее преобразование Лапласа, которое можно найти, записав преобразование Лапласа смещенной δ – функции:
L δ (t −t |
0 |
) = |
∞ |
δ |
(t |
−t |
0 |
)exp(−st )dt , |
(3.53а) |
|||
|
|
∫ |
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
которое, в соответствии с фильтрующим свойством δ |
– функции, дает |
|||||||||||
L |
δ (t |
−t |
0 |
) |
= exp(−st |
0 |
). |
(3.53б) |
||||
|
|
|
|
|
|
|
|
|
|
|
||
В случае, если δ – функция расположена в начале координат (смещение t0 = 0 ), то
L δ (t ) =1 |
(3.53б) |
|
|
|
|
Таким образом, спектральная плотность δ – функции равномерна на
всей S – плоскости. |
|
|
Предполагая, что сигнал |
x(t ) на входе цепи представляет собой |
δ – |
функцию, найдем выходной сигнал |
|
|
y(t )= ∞∫x(τ )h(t −τ )dτ = ∞∫δ (τ )h(t −τ )dτ = |
|
|
0 |
0 |
|
= ∞∫δ (t −τ )h(τ )dτ = h(t ), |
(3.54) |
|
0 |
|
|
используя фильтрующее свойство δ – функции. Из выражения (3.54)
следует, что, действительно, импульсная реакция h(t ) представляет собой отклик линейной цепи на δ – функцию. Выполнив преобразование Лапласа выражения (3.54), получим спектральную плотность выходного сигнала для данного случая
129

Y (s)= L δ (t ) H& (s)≡ H& (s).
Полученное выражение можно интерпретировать следующим образом: поскольку δ – функция обладает равномерным и равным единице спектром на всей S – плоскости, то спектральная плотность выходного сигна-
ла Y (s) тождественно равна передаточной функции системы. В этом слу-
чае обратное преобразование Лапласа от передаточной функции дает импульсную реакцию цепи.
Определим теперь импульсную реакцию простейших линейных цепей.
3.6.3.Импульсная реакция НЧ и ВЧ фильтров
Всоответствии с вышеизложенным, для определения импульсной реакции НЧ и ВЧ фильтров проделаем обратное преобразование Лапласа над их передаточными функциями. Так, для фильтра нижних частот можно записать
h(t )= L(−1) τ0 (s +11/τ0 ) .
Учитывая, |
что функция H (s) имеет единственный |
полюс в точке |
|||
sp = −1/τ0 |
и определяя соответствующий вычет k =1/τ0 , |
получим |
|||
|
h(t )= |
1 |
exp(−t /τ ). |
(3.55) |
|
|
|
||||
|
τ |
0 |
|
|
|
|
|
|
|
|
|
Импульсная реакция фильтра высоких частот представляет собой более сложную функцию. Для ее определения воспользуемся записью передаточной функции ВЧ – фильтра в форме (3.45)
H& (s)= |
sτ0 |
= |
sτ0 +1 −1 |
=1 − |
1 |
. |
|
1 + sτ0 |
1 + sτ0 |
|
τ0 (s +1 τ0 ) |
||||
130

Тогда импульсная реакция ВЧ – фильтра может быть определена как сумма обратных преобразований Лапласа
( ) |
|
[ ] |
τ |
0 |
(s + |
1 |
τ0 ) |
|
|
|
(−1) |
|
(−1) |
|
1 |
|
|
|
|
h t = L |
1 |
− L |
|
|
|
|
|
. |
|
Учитывая, что первое слагаемое есть обратное преобразование Лапласа равномерно распределенный по S – плоскости спектральной плотности,
получим функцию δ (t ). Второе преобразование дает функцию exp(−t /τ0 ).
Таким образом, импульсная реакция ВЧ – фильтра принимает вид
h(t )=δ (t )− |
1 |
exp(−t /τ0 ). |
(3.56) |
|
|||
|
τ0 |
|
|
Наличие δ – функции в составе импульсной реакции ВЧ – фильтра объясняет эффект обострения фронтов сигнала (эффект дифференцирования) при прохождении фильтра высоких частот.
3.6.4. Сопоставление спектрального метода и метода свертки при анализе линейных систем
Вышеизложенные результаты свидетельствуют о том, что функция времени на выходе фильтра может быть найдена как обратным преобразованием Лапласа над спектральной плотностью выходного сигнала, так и непосредственно во временной области с использованием интеграла свертки. В качестве примера приведем решение задачи определения формы сигнала на выходе линейной цепи с использованием обоих способов.
Зададим сигнал x(t )= exp(−αt ), обладающий преобразованием Лапласа
X (s)=1 (s +α), на входе фильтра нижних частот. В этом случае преобра-
зование Лапласа выходного сигнала определяется как
131
