1490

Далее, используя соотношения (5.38) и (5.39) выпишем отдельно спектральную плотность аналитического сигнала для областей отрицательных и положительных частот:

Из выражений (5.40) следует, что преобразование Фурье аналитического сигнала тождественно равно нулю в области отрицательных частот (ω < 0 ), а в области положительных частот (ω > 0 ) амплитудные значения спектральной плотности удваиваются. Полученный результат подтвержда-

ет, что выполнение одного из условий Титчмарша (функции x(t ) и σ (t )

являются сопряженными) повлекло за собой выполнение второго условия.

По известной спектральной плотности ψ& (t ) аналитического сигнала, его

зависимость во времени может быть найдена с использованием обратного преобразования Фурье

В порядке обсуждения результата (5.40) можно отметить, что его использование дает простой способ построения функции σ (t ), сопряжен-

ной к физически существующему сигналу x(t ). Исходная функция x(t )

должна быть подана на вход некоторого фильтра, обладающего равномерной амплитудно-частотной характеристикой, но вводящего фазовый сдвиг −π / 2 в области частот ω < 0 и +π / 2 в области частот ω > 0 . Такой фильтр называют квадратурным.

Рассмотрим теперь несколько примеров определения формы аналитиче-

ского сигнала ψ& (t ).

Пример 1. Определим аналитический сигнал ψ&1 (t ), отвечающий функции отсчетов

222

Данная функция была найдена обратным преобразованием Фурье от дей-

ствительной равномерной спектральной плотности X (ω), финитной на интервале (−ωB , ωB ). Для нахождения аналитического сигнала как функ-

ции времени воспользуемся выражением (5.41), т.е. обратным преобразо-

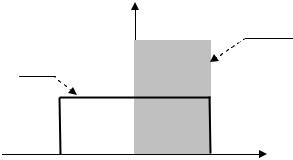
ванием Фурье над односторонней спектральной плотностью ψ&1 (ω) (см.

рис. 5.11).

ψ& (ω) ψ&1 (ω)

X1(ω)

2x0

x0

−ωB 0 ωB ω

Рис. 5.11. Спектральная плотность аналитического сигнала ψ&1 (ω)и

функции отсчетов x1 (t )

Пунктиром на этом рисунке обозначена спектральная плотность функции отсчетов x1 (t ). Тогда

223

представляет собой функцию, сопряженную к функции отсчетов x1 (t ).

Следует отметить, что вычисление функции σ1 (t ) путем применения пре-

образования Гильберта к функции x1 (t ) представляет собой весьма трудо-

емкий процесс. На рисунке 5. 12 изображены исходная функция x(t ) и

сопряженная к ней функция σ (t )

Рис. 5.12. Исходная функция x(t ) и сопряженная к ней функция σ (t )

Пример 2. Найдем аналитический сигнал ψ&2 (t ), отвечающий высокочас-

тотной функции отсчетов

используя вышеописанный метод. Спектральные плотности аналитическо-

го сигнала ψ&2 (t ) и физической функции x2 (t ) (пунктир) изображены на рисунке 5. 13.

Теперь аналитический сигнал ψ&2 (t ) можно найти как

Используя формулу Эйлера и известные тригонометрические соотношения

sinα −sin β = 2cos α + β sin α − β , 2 2

224

где ω0 = (ω1 +ω2 )/ 2 – средняя частота.

5.7.Узкополосные сигналы как частный случай сигналов

сограниченным спектром

Внастоящем подразделе рассматривается семейство так называемых узкополосных сигналов, имеющих место на выходе частотно-избирательных цепей, полоса пропускания (полоса прозрачности) ∆f которых, опреде-

ляющая ширину спектра выходного сигнала, много меньше центральной частоты ω0 полосы пропускания частотно-избирательной цепи

Условие (5.45) определяет принадлежность сигнала к семейству узкопо-

лосных. Если некоторая действительная функция x(t ) обладает спектраль-

ной плотностью, сосредоточенной в окрестности нулевой частоты, то функция y(t )= x(t )cos(ω0t +ϕ0 ) при достаточно большом значении часто-

Выражение (5.46а) представляет собой наиболее общую модель действительного узкополосного сигнала

226

где функции времени A(t )= x(t )cosϕ(t ), B(t )= x(t )sinϕ(t ) есть низко-

частотные функции, поскольку их относительные изменения за время, рав-

ла, а функция B(t ) называется квадратурной составляющей. В литературе также можно встретить определения, в соответствии с которыми обе функции A(t ) и B(t ) называются “квадратурными” составляющими (или компонентами) узкополосного сигнала, или его “косинусной” и “синусной” составляющими [20, 21, 27].

Отметим, что величина σ (t )=ω0t +ϕ(t ) есть полная фаза сигнала y(t )

и поэтому мгновенная частота этого сигнала определяется производной по

Из выражения (5.46а) следует также, что узкополосный сигнал представляет собой сложное колебание, обладающее одновременно как амплитудной, так и фазовой модуляцией несущего гармонического колебания, имеющего частоту ω0 .

Для определения формы аналитического сигнала ψ&Y , отвечающего дей-

ствительной узкополосной функции y (t ), найдем сопряженную функцию:

Здесь медленно меняющиеся функции A(t ) и B (t ) вынесены за знак ин-

ной, равной нулю) и получим

227

бающей и фазой физической функции y (t ) соотношениями

228

ϕ(t )= arctg BA((tt )); argψ&Y (t )= arctg BA((tt )).

Из выражения (5.50) следуют частные соотношения для преобразования Гильберта гармонических функций:

5.8. Теорема отсчетов для полосового сигнала.

Рассмотрим теорему отсчетов во временном представлении примени-

тельно к функции x1 (t ), обладающей комплексной спектральной плотно-

приведено на рис. 5.14.

Рис. 5.14. Спектральная плотность полосового сигнала

Сопоставим функции x1 (t ) аналитический сигнал в соответствии с пра-

вилом (5.41):

229

есть функция, сопряженная к x1 (t ).

Используя прием периодического продолжения, разложим спектраль-

где величина ω2 −ω1 = ∆ω (ширина спектральной полосы) принята за пери-

од, а коэффициенты ряда определяются как

Учитывая, что аналитический сигнал ψ& (t ) связан со спектральной плот-

ностью X& (ω) соотношением

230

Тогда, подставляя ряд Фурье (5.55) в соотношение (5.57), получим

Рассмотрим теперь физическую функцию x1 (t ), представляющую собой действительную часть аналитического сигнала ψ& (t ). Для простоты рас-

смотрим только действительную часть одного из слагаемых ряда (5.61):

231