1490

Рассмотрим теперь способ обойти проблему, возникающую в случае, если интеграл (3.1) расходится. Введем для этого вместо функции x(t) зату-

хающую функцию x(t)exp(−σt ) с параметром σ >0 и найдем ее спек-

тральную плотность, которая будет зависеть от параметра σ [15]:

Вследствие быстрого убывания множителя exp(−σt ) при t →∞ интеграл

(3.3) сходится даже для таких функций как tn , а также для показательной

функции exp(αt) (α >0) , если выбрать параметр σ >α . Таким образом,

использование функции x(t)exp(−σt) вместо функции x(t) позволяет уст-

ранить расходимость интеграла (3.1) практически для всех анализируемых функций. Выражение (3.2) может быть переписано в виде:

(Последнее выражение получено путем умножения обоих частей равенства

(3.4) на exp(−σt )).

Из выражений (3.5) и (3.6) видно, что параметр σ и частота ω входят в эти выражения в виде комбинации σ + jω . Таким образом, появилась ком-

плексная переменная, которую можно обозначить одной буквой:

93

s =σ + jω . Поскольку функция X&σ (ω) зависит от этой новой переменной,

введем обозначение X&σ (ω) = X& (σ + jω) = X (s) . Необходимо отметить, что в литературе по преобразованию Лапласа часто вместо s используют обозначение p , заимствованное из работ Оливера Хевисайда. Однако у Хеви-

сайда буква p означает не переменную, а некоторый дифференциальный

оператор. Кроме того, в математике при одновременном рассмотрении двух переменных принято применять для их обозначения две соседние буквы алфавита (например, x и y , u и v и.т.д.).

Тогда, поскольку аргументом функции x(t) является время t , то для обозначения нового аргумента функции x(σ + jω) целесообразно выбрать

букву s . Иногда переменную s называют комплексной частотой [8, 16, 17], однако с физической точки зрения это не имеет смысла, так как во всех случаях речь может идти только о вещественных частотах, определяемых значениями Im s =ω , а величина Re s =σ есть параметр, определяющий скорость затухания функции x(t) , определяемую экспонентой exp{−σt}.

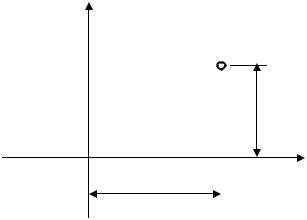
Теперь введем переменнуюs вместо частоты ω в выражение (3.6) как переменную, по которой производится интегрирование. Поскольку в этом выражении частота ω изменяется от −∞ до +∞, в то время как величина σ остается постоянной, то переменная s =σ + jω будет изменяться в пре-

делах от σ − jω до σ + jω . Этому изменению переменной s на комплекс-

ной плоскости соответствует перемещение вдоль прямой, параллельной оси ординат Im s =ω . Абсцисса этой прямой определяется отрезком σ действительной оси Re s =σ (см. рис. 3.1)

94

Поскольку в выражении (3.6) проведена замена переменных ω →s , то

Рис 3.1. Контур интегрирования на комплексной плоскости

Выражение (3.7) называется прямым преобразованием Лапласа, а выражение (3.8) представляет собой обратное преобразование Лапласа. Физический смысл преобразования Лапласа можно изложить следующим образом:

Если в функции X (s) , определяемой прямым преобразованием Лапласа

(3.7), рассматривать аргумент s как комплексную переменную s =σ + jω ,

то функция X (σ + jω) при постоянном значении σ будет представлять собой спектральную плотность затухающей функции времени

95

exp{−σt}x(t) . Функция времени x(t) может быть построена по спектраль-

ной плотности X (s) с использованием выражения (3.8).

Рассматриваемое преобразование было найдено французским математиком Пьером Симоном де Лапласом, который указал на взаимно однозначное соответствие функций x(t) X (s) , и применил результаты для решения дифференциальных уравнений. При использовании этого преобразования дифференциальные уравнения переходят в алгебраические, что значительно упрощает решение. Однако ценность этого преобразования для решения прикладных задач оставалась неизвестной более ста лет, пока в конце 19 века его, по существу, вновь не открыл Оливер Хевисайд. Исследования Хевисайда оказали значительное влияние на современную электротехнику, а затем и на радиотехнику.

3.2Основные свойства преобразования Лапласа

Внастоящем параграфе рассматриваются основные свойства преобразования Лапласа [14 - 17] с использованием простых примеров и будет показано, что основные свойства преобразования Лапласа по своему смыслу идентичны свойствам преобразования Фурье, что согласуется с результатами, изложенными в предыдущем параграфе.

3.2.1Область сходимости

Если при каком – либо значении σ0 параметра σ спектральная плот-

ность затухающей функции exp(−σ0t)x(t) существует, то очевидно, что она существует и при значении параметра σ >σ0 . Математически это означает,

что если интеграл (3.7) сходится при значении s =σ0 + jω , то он сходится

96

также при s =σ + jω , где σ >σ0 . Очевидно, что если функция x(t) не име-

ет особенностей, то областью сходимости интеграла (3.7) является полуплоскость Re[s] >σ0 . Минимальное действительное число σ0 , при котором интеграл сходится, называется абсциссой абсолютной сходимости. Область абсолютной сходимости может занимать всю s – плоскость, так что σ0 =−∞. Это справедливо, например, для короткого импульса x(t) , нерав-

ного нулю лишь на конечном интервале времени.

Отметим, что большинство функций спектральной плотности X (s) ,

представляющих для нас интерес, являются рациональными функциями , то есть отношениями полиномов переменной s различной степени. Особый интерес представляют правильные рациональные функции, для которых степень полинома числителя меньше или равна степени полинома знаменателя. Корни полинома числителя, обращающие функцию X (s) в

нуль, называются нулями рациональной функции, а корни полинома знаменателя, обращающие функцию X (s) в бесконечность, называются по-

люсами функции. По определению, в области сходимости не может быть полюсов и поэтому для рациональной функции X (s) областью сходимости является область, лежащая правее самого правого полюса.

Рассмотрим теперь несколько примеров.

Пример 1. Зададим функцию времени в виде:

1 при t > 0, x(t) = 0 при t < 0.

Эта функция называется функцией единичного скачка или единичным скачком Хевисайда (рис 3.2). Вопрос об определении функции x(t) в точке разрыва t =0 оставим открытым, так как при вычислении преобразования Лапласа безразлично, какое значение имеет эта функция при t =0 . Тогда

97

X (s)= ∞∫x(t )exp(−st )dt =

0

Re[s] =σ >0 . Таким образом, областью сходимости функции X (s) являет-

ся полуплоскость.

x(t )

1

t

0

Рис 3.2. Единичный скачок Хевисайда

Таким образом, абсциссой абсолютной сходимости в данном случае является величина −α .

98

Пример 3. Найдем преобразование Лапласа функции x(t) =cosωt , заданной на интервале t >0 .

представляющей собой один полупериод функции sinω0t . Тогда

X (s) =π∫/ ω sinωt exp(−st )dt =

0

99

существующий для всех значений s . Функция (3.13б) не имеет полюсов ни в одной точке s – плоскости, поскольку полюса в точках s =± jω компен-

сируются в этих точках нулями этой функции, т.е. значениями s =± jω , которые являются корнями числителя, т.к. 1 +exp(−sπ /ω)S =± jω = 0.. Не-

трудно видеть, что в точках s = ± jω имеет место неопределенность типа

0 / 0 , раскрывая которую по правилу Лопиталя, получим после первой же процедуры дифференцирования числителя и знаменателя

Таким образом, область сходимости в данном случае представляет собой всю комплексную плоскость. Это справедливо в силу того, что функ-

100

ция x(t) представляет собой импульс синусоидальной формы, определен-

ный на конечном интервале времени.

В дальнейшем, как правило, указание области сходимости будет опускаться, но при этом, естественно, будет подразумеваться, что существуют некоторое значение σ0 , такое, что для Re[s] >σ0 все интегралы, имеющие место в конкретной задаче, сходятся.

3.2.2. Теорема задержки (смещения), теорема линейности и их использование

Теорема задержки и теорема линейности для преобразования Лапласа идентичны по смыслу соответствующим теоремам для преобразованиям Фурье. Рассмотрим эти теоремы на конкретных примерах.

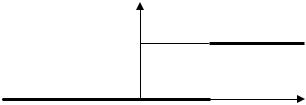
Пример 1. Рассмотрим преобразование Лапласа смещенной функции

1 при t > Τ x(t −Τ) = 0 при t <Τ,

которая изображена на рис 3.3.

при условии, что Re[s] =σ > 0, так что exp(−st )→0 при t →∞.

101