U |
(t) = A Re |
exp( |
jω t ) |
∞ |
J |
|
(m )exp( jkΩt ) |
= |
∑ |
k |
ЧМ |
0 |
|
|
|
0 |
k=−∞ |
|
|
ЧМ |
|
|
|
|
|
|
|
|
|
|
|
|
= A |
∞ |
J |
|
(m)cos(ω |
|
+ kΩ)t. |
|
(6.43) |
|
∑ |
k |
|
|
|
0 k=−∞ |
|
|
0 |
|
|
|
|
|
Набор значений функций Бесселя Jk (m) образует спектр ЧМ сигнала. Не-
трудно видеть, что спектр ЧМ сигнала с однотональным сообщением содержит в общем случае бесконечное число боковых колебаний cos(ω0 ±kΩ)t . Поскольку функции Бесселя с положительными и отрица-
тельными значениями порядка k связаны соотношением [31]
J |
−k |
(m) = (−1)k J |
k |
(m) , |
|
|
|
|
|
то начальные фазы боковых колебаний с частотами |
ω0 + kλ и ω0 −kΩ |
совпадают для четных k и отличаются на 1800 для |
нечетных k . Факт |
изменения фазы нечетных номеров нижних боковых колебаний на 1800 по сравнению с соответствующими верхними боковыми колебаниями был продемонстрирован выше для значений m <<1и m ≈1.
В таблице 6.1 приведены значения функций Бесселя различных порядков в зависимости от индекса модуляции [30]. Из этой таблицы следует, что с ростом индекса функции Бесселя увеличивается протяженность области аргументов, при которых значения функции (т.е спектральные коэффициенты) очень малы.
Таким образом, хотя с ростом индекса модуляции ширина полосы частот, занимаемая ЧМ сигналом, расширяется, но, начиная с некоторого номера k , значениями спектральных коэффициентов Jk (m) можно пренеб-
речь. Обычно принято пренебрегать спектральными коэффициентами, начиная с величины функции Бесселя k > m +1. Отсюда следует, что реаль-
ная ширина спектра ЧМ сигнала может быть оценена как |
|
∆F = 2(m +1)Ω. |
(6.44а) |
|
|
|
|
|
|
|
|
Таблица 6.1. |
|
|
|
|
|
|
|
|
|
|
k \ m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0,765 |
0,224 |
-0,26 |
-0,397 |
-0,177 |
0,15 |
0,3 |
0,17 |
|
1 |
0,44 |
0,576 |
0,339 |
-0,066 |
-0,327 |
-0,276 |
-0,004 |
0,234 |
|
2 |
0,115 |
0,353 |
0,486 |
0,364 |
0,046 |
-0,243 |
-0,3 |
-0,113 |
|
3 |
0,0195 |
0,129 |
0,309 |
0,43 |
0,365 |
0,115 |
-0,167 |
-0,291 |
|
4 |
0,0025 |
0,034 |
0,132 |
0,281 |
0,391 |
0,357 |
0,158 |
-0,105 |
|
5 |
|
0,07 |
0,043 |
0,132 |
0,261 |
0,362 |
0,348 |
0,186 |
|
6 |
|
0,001 |
0,0114 |
0,049 |
0,131 |
0,246 |
0,34 |
0,337 |
|
7 |
|
|
0,002 |
0,015 |
0,053 |
0,129 |
0,233 |
0,32 |
|
8 |
|
|
|
0,004 |
0,018 |
0,056 |
0,128 |
0,235 |
|
9 |
|
|
|
|
0,005 |
0,021 |
0,058 |
0,126 |
|
10 |
|
|
|
|
0,001 |
0,007 |
0,023 |
0,06 |
|
11 |
|
|
|
|
|
0,002 |
0,008 |
0,025 |
|
12 |
|
|
|
|
|
|
0,002 |
0,009 |
|
13 |
|
|
|
|
|
|
0,001 |
0,003 |
|
14 |
|
|
|
|
|
|
|
0,001 |
|
15 |
|
|
|
|
|
|
|
0,0003 |
|
Как правило, на практике индекс частотной модуляции удовлетворяет ус-
ловию mЧМ >>1. Тогда (6.44а) можно переписать в виде |
|
∆F ≈ 2mЧМ Ω = 2∆ω , |
(6.44 б) |
поскольку mЧМ = ∆ω/ Ω.
Таким образом, ЧМ сигнал занимает полосу частот, определяемую удвоенной величиной девиации частоты ∆ω .
6.3.6. Спектр фазо - манипулированного сигнала
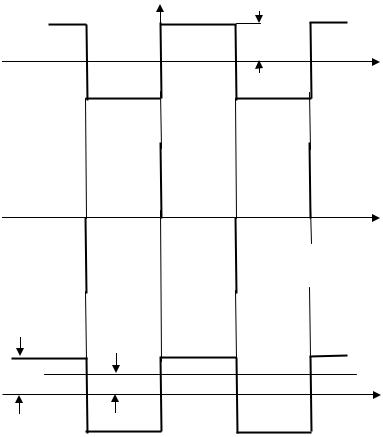
Фазовая манипуляция радиосигналов представляет собой один из видов фазовой модуляции, при которой имеют место скачкообразные (мгновенные) изменения фазы радиосигнала в соответствии некоторым заданным правилом [7, 11] (например – предаваемым сообщением).
Рассмотрим закон изменения фазы при ее периодическом изменении, имеющим “прямоугольный” характер (рис 6.12). Внутри этого периода мо-
дуляции (см. рис 6.12а) изменение фазы описывается следующим условием:
ϕ |
MAX |
при 0 <t ≤T / 2 |
(6.45) |
ϕ(t) = |
|
при T / 2 <t ≤T |
−ϕMAX |
|
|
|
|
ϕ(t ) |
|
|
|
|
ϕMAX |
|
−T / 2 |
|
0 |
T / 2 |
t |
|
T |
a)
2ϕMAX δ (t )
|
−T / 2 |
0 |
T / 2 |
T |
t |
|
|
|
−2ϕMAX δ (t +T / 2) |
|
|
−2ϕMAX δ (t −T / 2) |
|
|
|
|
б) |
|
|
|
|
|
sinϕ |
|
|
|
sinϕMAX |
cosϕMAX |
|
|
t |
|
−T / 2 |
0 |
T / 2 |
T |
|
|
в)
Рис. 6.12. Закон изменения фазы
Изменение частоты колебания ∆ω(t) , определяемое как
∆ω(t) = dϕ(t) / dt , имеет вид, показанный на рис. 6.12б. При этом величина
∆ω(t) равна нулю на всей |
оси времени t , исключая точки |
t =0; t = ±T / 2; t = ±T; ... t = nT / 2 , |
в которых функция ϕ(t) имеет разрыв. В |
этих точках, как это следует из правил дифференциального исчисления, ∆ω(t) обращается в бесконечность, что, с точки зрения теории обобщен-
ных функций, соответствует знакопеременной последовательности дельта-
функций, умноженных на некоторый постоянный коэффициент γ . Коэф-
фициент γ определяется из условия совпадения интеграла от функции
∆ω(t) с заданным законом изменения фазы [11].
Так, для момента времени t =0 можно получить следующее условие:
T∫/ 2 |
∆ω(t)dt =T∫/ 2 |
γδ (t )dt = 2ϕMAX ,, |
−T / 2 |
−T / 2 |
|
откуда, с учетом условия нормировки |
|
T∫/ 2 δ (t )dt =1
−T / 2
следует, что γ = 2ϕMAX . Таким образом, в момент времени t = 0 изменение частоты должно быть представлено функцией 2ϕMAX δ(t) . В моменты вре-
мени t = ±T / 2 изменение частоты определяется как −2ϕMAX δ(t ±T / 2) .
Учитывая выражение (6.35), представляющее колебание с угловой модуляцией (в данном случае – с фазовой манипуляцией) в виде суммы квадратур
UФМ (t )= A0 cosϕ(t )cosω0t − A0 sinϕ(t )sinω0t,
напомним, что спектр сигнала UФМ (t) определяется спектрами функций cosϕ(t) , sinϕ(t) и определим эти спектры. Графики функций cosϕ(t) и sinϕ(t) изображены на рис. 6.12в.
Поскольку ϕ(t) есть нечетная функция времени, постоянная на интер-
валах 0 <t <T / 2 и −T / 2 < t < 0 , то cosϕ(t) = cos[−ϕ(t)]= cosϕMAX = const ,
а функция sinϕ(t) имеет вид прямоугольного периодического сигнала с амплитудой sinϕMAX .
Для выбранного на рис 6.12в начала отсчета функция sinϕMAX является нечетной и поэтому разложение данной функции в ряд Фурье содержит только коэффициенты bk (см. главу 1). Найдем эти коэффициенты в виде

|
|
|
|
|
|
b = |
2 |
T∫/ 2 |
sinϕ(t)sin nΩtdt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
T −T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
∫0 (−sinϕMAX )sin nΩtdt + |
2 |
|
T∫/ 2 sinϕMAX sin nΩtdt = |
|
|
|
|
T |
|
|
|
|
|
|
|
−T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 0 |
|
|
|
|
= |
2sinϕMAX |
cos nΩt |
|
0 |
|
|
−cos nΩt |
|
T / 2 = − |
4sinϕMAX |
cos nΩT / 2 −1 . |
(6.46) |
|
|
|
|
|
|
|
|
TnΩ |
|
|
|
|
|
|
|
−T / 2 |
|
|
|
|
|
|
|
0 |
|
|
|
TnΩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
nΩT / 2 = n |
2π |
T = nπ , то коэффициенты b |
существуют только |
|
|
|
|
|
|
|
|
|
|
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для нечетных значений n , т.к. cosnπ =0 |
|
при n = 0, |
2, 4... , а cos nπ = −1 |
при n =1, |
3, |
5.... Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = |
|
8sinϕMAX |
|
|
= |
8sinϕMAX |
|
= |
4sinϕMAX |
|
|
(6.47) |
|
|
|
|
|
|
|
|
|
|
|
Tn2π /T |
|
|
|
|
|
|
|
|
k |
|
|
TnΩ |
|
|
|
|
|
|
πn |
|
|
|
|
для n =1, |
3, |
5... и bk |
= 0 для n =0, 2, 4.... |
|
|
|
|
|
|
|
|
Таким образом, разложение функции sinϕ(t) в ряд Фурье имеет вид |
|
|
|
sinϕ(t) = |
4sinϕMAX |
|
sin Ωt +1 sin3Ωt +1 sin 5Ωt +... . |
(6.48) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перенесем теперь спектры функций cosϕ(t) и sinϕ(t) на соответст-
вующие квадратурные составляющие cosω0t и sinω0t . Косинусную квад-
ратуру запишем в виде |
|
|
|
A0 cosϕ(t)cosω0t = A0 cosϕMAX cosω0t , |
(6.49а) |
а синусную квадратуру как |
|
|
|
A0 sinϕ(t)sinω0t = |
4 |
A0 sinϕMAX |
sin Ωt sinω0 t + |
|
|
|
π |
|
|
|
+13sin3Ωt sinω0t +15 sin 5Ωt sinω0t +...] =
=π4 A0 sinϕMAX 12 cos(ω0 −Ω)t − 12 cos(ω0 +Ω)t + 16 cos(ω0 −3Ω)t −16 cos(ω0 +3Ω)t +
+ |
1 |
cos(ω0 |
−5Ω)t − |
1 |
(ω0 +5Ω)t +...] . |
(6.49б) |
|
|
10 |
|
10 |
|
|

Выражения (6.49) и (6.35) позволяют записать окончательную форму спектрального разложения фазо – манипулированного колебания:
UФМ (t) = A0 {cosϕMAX cosω0 t + |
2 |
sinϕMAX [cos(ω0 |
+ Ω)t −cos(ω0 −Ω)t]+ |
π |
+ |
2 |
sinϕ |
|
|
cos(ω +3Ω)t −cos(ω −3Ω)t + |
|
3π |
|
|
|
|
|
|
|
MAX |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
+ |
2 |
|
sinϕ |
|
|
cos(ω +5Ω)t −cos(ω −5Ω)t +...}. |
(6.50) |
5π |
|
|
|
|
|
|
|
MAX |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Значительный интерес для практики представляет случай |
ϕMAX =0,5π , |
когда полный скачок фазы равен π , а фазо – манипулированное колебание принимает вид, показанный на рис. 6.13
|
|
U (t ) |
A0 |
|
t |
|
0 |
|
|
−T / 2 |
|
T / 2 |
Рис. 6.13. ФМ сигнал в случае полного скачка фазы, равного π |
Как следует из этого рисунка, скачок фазы на 1800 происходит через каждую половину периода закона модуляции. При этом cosϕMAX = 0 , sinϕMAX =1 и выражение (6.50) для спектрального представления фазо-
манипулированного сигнала принимает вид
UФМ (t) = |
2A0 |
{[cos(ω0 + Ω)t −cos(ω0 −Ω)t]+ 1 |
[cos(ω0 +3λ)t −cos(ω0 −3λ)t]+ |
|
π |
3 |
|
|
|
|
+1 [cos(ω0 +5λ)t −cos(ω0 −5λ)t |
]...}. |
(6.51) |
|
|
5 |
|
|
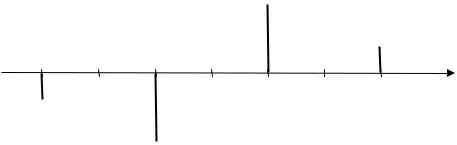
Спектр этого колебания (до боковых частот ω0 ±3Ω) |
изображен на рис. |
6.14. Кроме того, из выражения (6.51) следует, что спектральная амплитуда на частоте ω =ω0 равна нулю. Таким образом, при манипуляции фазы с полным скачком ϕ =π (ϕMAX = 0,5π ) несущая частота в спектре фазо – ма-
нипулированного колебания отсутствует.
2A0 /π
|
ω −3Ω |
ω −Ω |
2A0 / 3π |
|
|
0 |
0 |
ω0 +3Ω |
ω |
|
−2A0 / 3π |
ω0 ω0 +Ω |
|
|
−2A0 /π
Рис. 6.14. Спектр фазо – манипулированного колебания для случая полного скачка фазы, равного π
6.4. Импульсные радиосигналы с внутриимпульсной модуляцией. Сжатие сигналов по оси времени
В настоящем подразделе рассмотрены спектральные и корреляционные свойства импульсных радиосигналов, высокочастотное заполнение которых модулировано по частоте. Чаще всего используется внутриимпульсная ЧМ с линейным законом изменения частоты во времени.
Теория таких сигналов и соответствующие технические способы их создания и обработки были созданы вскоре после окончания второй мировой войны одновременно в СССР (Я. Ширман) [32] и в США (Ф. Вудворд и др.) [33]. В качестве основных причин, обусловивших эти разработки, явилась необходимость обеспечения одновременных измерений радиальной составляющей скорости радиолокационного объекта (доплеровский сдвиг частоты) и дистанции до него с высокой разрешающей способностью по обоим параметрам. Однако высокое разрешение по скорости требует использование радиосигнала (импульса), имеющего большую длительность, а высокое разрешение по дальности, напротив, требует минимальной протяженности импульса во времени. В данном случае соотношение неопределенности ∆f ∆τ =1 привело к противоречию интересов при разработке РЛС и к необходимости синтеза нового класса сигналов, способных одновременно обеспечить высокое разрешение как по дальности,
268
так и по скорости. Проведенные исследования и разработки показали, что длительность радиолокационного сигнала может быть настолько велика, чтобы удовлетворить требования к разрешению по скорости, а высокое разрешение по дальности может быть при этом обеспечено за счет внутриимпульсной широкополосной модуляции (ЧМ или ФМ). Новый класс сигналов получил название «сложные сигналы». Использование данных сигналов позволяет обеспечить оптимальность радиолокационных систем, но эти вопросы не входят в круг интересов данного пособия.
6.4.1. Спектр радиосигнала с внутриимпульсной частотной модуляцией.
Рассмотрим спектральный состав прямоугольного радиоимпульса [1, 32, 33], обладающего значительной длительностью τИ , полагая при этом,
что частота его заполнения линейно нарастает во времени. Будем считать также, что начало координат t = 0 соответствует середине импульса (рис. 6.15).
|
U (t ) |
|
−τИ / 2 |
0 |
t |
|
|
|
τИ / 2 |
Рис. 6.15
Для определения математической модели радиосигнала U (t )= cos ψ (t )
с внутриимпульсной ЧМ необходимо определить закон изменения обоб-
щенной фазы ψ (t ) во времени. Для этого запишем закон линейного изме-
нения угловой частоты во времени как
где ω0 = 2π f0t – несущая частота, отвечающая |
моменту времени |
t = −τИ / 2, а величина |
|
µ = ∆ω/τИ |
(6.53а) |
представляет собой скорость изменения угловой частоты во времени. Максимальное изменение частоты за длительность импульса составляет
|
|
|
|
|
|
∆ω = µτИ. |
(6.53б) |
Найдем обобщенную (полную) фазу ЧМ сигнала U (t )= cos ψ (t ) |
|
|
( |
|
) |
|
t |
] |
0 |
|
|
ψ |
t |
= |
∫[ 0 |
(6.54) |
|
|
|
ω |
+ µt ' dt ' =ω t + µt2 / 2 |
|
|
|
|
|
|
0 |
|
|
|
и запишем математическую модель радиосигнала с линейной |
внутриим- |
пульсной ЧМ в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 при t < −τИ / 2; |
|
U |
|
|
|
|
|
|
|
при −τИ / 2 ≤ t ≤τИ / 2; |
(6.55) |
ЛЧМ (t )= UM cos(ω0t + µt2 / 2) |
|
|
|
|
|
|
|
0 при t <τИ / 2. |
|
|
|
|
|
|
|
|
|
Используя математическую модель (6.55), запишем спектральную плот-
ность одиночного ЛЧМ импульса: |
|
|
|
|
|
|
|
|
|
|
|
|
S (ω)=UM τИ∫/ 2 |
cos(ω0t + µt2 / 2)exp(− jωt )dt = |
|
|
|
−τИ / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
τИ / 2 |
|
{ |
|
|
|
|
0 |
|
|
} |
|
|
|
∫ |
|
|
|
|
|
|
|
|
= 0,5U |
|
|
exp |
|
j |
|
(ω −ω)t + 0,5µt |
2 |
|
dt + |
|
|
|
|
|
|
|
|
|
|
|
−τИ / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
τИ / 2 |
|
{ |
|
|
|
|
0 |
|
|
|
|
} |
|
|
∫ |
|
|
|
|
|
|
|
|
|
+0,5U |
|
|
exp |
|
− j |
|
(ω |
+ω)t + 0,5µt |
2 |
|
dt. |
(6.56) |
|
|
|
|
|
|
−τИ / 2
Спектральная плотность ЛЧМ импульса в области положительных частот описывается первым интегралом выражения (6.56). Вычислим этот интеграл. Для этого преобразуем показатель подынтегральной экспоненциальной функции и дополним его до полного квадрата:
|
|
2(ω − |
ω |
)t |
|
0,5µt2 −(ω −ω0 )t = 0,5µ t2 |
− |
|
0 |
|
|
= |
µ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(ω −ω )t |
|
(ω |
−ω )2 |
|
(ω − |
ω )2 |
|
|
|
|
= 0,5µ t2 |
− |
|
|
|
|
0 |
+ |
|
|
0 |
|
|
− |
|
|
|
|
|
0 |
|
= |
|
|
|
|
µ |
|
|
|
µ2 |
|
|
|
|
|
|
µ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ω |
− |
ω )2 |
|
|
|
|
2 |
(ω − |
ω )t |
|
|
(ω −ω )2 |
|
|
= −0,5µ |
|
|
0 |
|
|
|
+ 0,5µ t2 − |
|
|
|
0 |
|
|
+ |
|
|
|
0 |
|
|
= |
|
µ |
|
|
|
|
µ |
|
|
|
|
|
|
µ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−0,5µ ( |
ω −ω |
2 |
|
|
|
|
|
ω |
−ω |
0 ) |
|
2 |
|
|
|
(6.57) |
|
|
|
0 ) |
+ 0,5µ |
t − ( |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
Подставляя (6.57) в первый интеграл выражения (6.56), запишем спектральную плотность ЛЧМ импульса в области положительных частот как
|
(ω −ω0 )2 τИ / 2 |
|
µ |
ω −ω0 |
S&ЛЧМ (ω)= 0,5UM exp − j |
2µ |
|
|
∫ |
|
exp j |
2 |
t − |
|
|
|
µ |
|
|
−τ |
/ 2 |
|
|
|
|
|
|
И |
|
|
|
|
|
Для вычисления интеграла выражении (6.58) воспользуемся заменой переменной в соответствии с выражением
|
ω −ω |
|
= |
π x, |
(6.59) |
µ t − |
0 |
|
|
µ |
|
|
|
|
откуда следует, что
t − |
ω −ω |
0 = |
π |
x, dt = |
π |
|
ω −ω |
|
2 |
µ |
µ |
µ |
dx, 0,5µ t − |
µ |
0 |
|
= 0,5πx2. |
|
|
|
|
|
|
|
При использовании данной замены переменных пределы интеграла (6.58) принимают вид
|
|
|
−X1 = |
µ τ |
|
|
+ |
ω −ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
µ |
0 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
|
|
|
|
|
|
|
|
|
τ |
µ |
|
|
ω −ω0 |
|
|
|
0,5µτ |
И |
+ |
( |
ω −ω |
0 ) |
|
|
|
= |
0,5 |
И |
|
+ |
|
|
= |
|
|
|
|
|
|
, |
6.60а) |
|
π |
|
|
|
|
|
π |
|
µ |
|
|
|
|
|
|
π |
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 = |
µ τ |
И − |
ω −ω |
|
= |
|
|
|
|
|
|
|
|
|
|
|
µ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
2 |
|
|
|
|
|
|
|
|
|
|
|