
10.4. Обобщенные координаты, число степеней свободы механической системы
Принцип возможных перемещений применяется для описания движений сложных механических систем. Сложность механической системы характеризуется числом обобщенных координат.
Обобщенными координатами называют независимые величины, заданием которых однозначно определяется положение всех точек механической с стемы.
10.4.1. Механ ческая система с одной степенью свободы |
С |
представлен |
|
|
|
На |
р с. |
10.4 |
|
|
|
кривош пно-ползунный |
механизм, |
|
|
|
имеющ й размеры ОА=r; |
АВ=l. |
|
|
|
|
Угол в данном механизме |
|
|
|
является |
|
|
|
|
|
, |
|
|
|
координатой |
|
|
|
|
с помощью |
которой |
можно |
|
|
|
определ ть коорд наты всех точек |
|
|
|
механизма: |
|
|
|
|
|
|
|
|
xA r cos ; |
yA |
r sin ; |
|
|
|
|
обобщенной |
|
|
|
x |
В |
ОК КВ r cos l 2 |
r 2 sin2 ; |
y |
B |
0 . |
Таким образом, Амы видим, что координаты точек системы являются
10.4.2.Механическая системаДсо многими степенями свободы
Вкачестве примера сложной механическойИсистемы рассмотрим случай свободного движения твердого тела (рис. 10.5).
Вобщем случае движение свободноготвердогопоступательноецентром
полюс, и сферическое движение тела относительно центра масс. Поступательное движение тела происходит вместе с системой координат Сx1 y1z1 , которая перемещается
параллельно инерциальной системе координат О1x1y1z1.

При поступательном перемещении центр масс тела С перемещается по траектории, уравнение которой в пространстве определяется тремя
обобщенными координатами: |
хс=f1(t); |
ус=f2(t); zс=f3(t). |
|
|
ферическое движение тела относительно центра масс определяется |
тремя углами Эйлера: ψ=f4(t); |
=f5(t); |
=f6(t), где ψ – угол прецессии; – |
С |
|
|
|
|
|
|
|
|
угол нутации; |
– угол собственного вращения. |
|
|
В аналитической механике обобщенные координаты принято |
обозначать qi, где i – индекс (номер) обобщенной координаты. Для |
свободного твердого тела обобщенные координаты имеют вид |
|
|
q1=хс; |
q2=yс; q3=zc; |
q4=ψ; |
q5= ; |
q6=φ. |
|
механическ |
|
|
|
|
|
|
10.5. Пр нц п возможных перемещений для механической |
|
|
|
с стемы, находящейся в равновесии |
|
В |
б |
находиться неподвижные |
состоян |
|
равновесия |
|
могут |
|
е с стемы, а также системы, находящиеся в движении. |
|
Представ м |
|
неподвижную |
|
|
|
механическую |
|
с стему |
в |
|
виде |
|
|
|
совокупности точек, на которые |
|
|
|
действуют задаваемые силы и реакции |
|
|
|
связей (рис. 10.6). Механическая система |
|
|
|
состоит из n материальных точек и имеет |
|
|
|
S степеней |
свободы. Каждая точка |
|
|
|
механической |
|
системы |
|
Д |
|
|
подчинена |
|
|
|
идеальным стационарнымАдвусторонним |
|
|
связям и находится в равновесии. |
|
|
|
|
|
|
Для точек механической системы справедливы уравнения |
равновесия |
|
Рi |
Ri 0 , |
i=1,2,…,n или Рi Ri |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
И |
где Pi |
– равнодействующая задаваемых сил, приложенных к точке; Ri – |
равнодействующая сил реакций связей. |
|
|
|
|
Мысленно сообщим системе возможное перемещение по одной |
обобщенной координате, приняв постоянными все другие обобщенные |
координаты. В результате точки механической системы получают |
соответствующие |
возможные перемещения |
si . Вычислим |
сумму |
элементарных работ всех сил механической системы на всех возможных |
перемещениях: |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
si ) |
n |
|
|
|
(10.6) |
|
|
Pi si cos(Pi , |
Ri si cos(Ri , si ) 0 . |
|
|
i |
1 |
|
|
|
i 1 |
|
|
|
|
Принимая, что все связи механической системы являются идеальными, а все силы трения, если они имеются, переведены в разряд задаваемых сил, можем утверждать, что сумма работ идеальных связей механической системы равна нулю:
С |
n |
|
(10.7) |
Ri si cos(Ri , si ) 0 . |
i 1 |
|
|
|
|
|
Это означает, что |
при записи суммы |
элементарных работ в |
уравнении (10.6) работу идеальных связей можно не рассматривать. Тогда |
уравнен е, выражающее принцип возможных перемещений для |
механической с стемы, будет иметь вид |
|
|
системы |
|
|
|
|
|
|
n |
|
|
|
(10.8) |
|
|
Pi si cos(Pi , si ) 0. |
|
|
|
i 1 |
|
|
|
|
|
|
ущность пр нц па возможных перемещений, согласно уравнению |
(10.8), состо т в следующем: для равновесия голономной механической |
|
обобщенной |
|
идеальным, |
|
со |
мног ми степенями |
свободы, подчиненной |
стационарным |
неосво ождающим связям, необходимо и достаточно, чтобы |
сумма элементарных ра от всех задаваемых сил, приложенных к точкам |
системы, была равна нулю на лю ом возможном перемещении системы по |
заданной |
|
координате. |
|
|
|
|
|
|
|
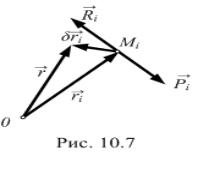
А |
|
Если для точек механической системы |
|
|
возможные перемещения задать |
|
изменением |
|
|
радиуса-вектора (рис. 10.7), проведенного из |
|
|
произвольной точки О, то уравнение, |
|
|
выражающее |
принцип |
|
возможных |
|
|
перемещений, будет иметь вид |
|
Д |
|
n |
|
|
|
|
(10.9) |
|
|
|
Pi ri cos(Pi , ri ) 0 . |
|
|
|
|
i 1 |
|
|
|
|
|
|
Уравнение можно записать в виде скалярного произведения векторов |
|
|
|
|
|
n |
|
|
(10.10) |
|
|
|
|
|
Pi ri 0. |
|
|
|
|
|
|
|
|
И |
i 1
Полученные уравнения (10.8) – (10.10) можно использовать для решения задач статики на равновесие механических систем.
10.6. Методы решения задач аналитической механики
10.6.1. Геометрический метод
Геометрический метод предполагает вычисление работ активных сил на возможном перемещении механической системы. При поступательном
движении тела элементарная работа постоянной силы Fk на возможном перемещении δsk определяется по формуле
Аk Fk sk cos(Fk , sk ).
При вращении тела вокруг неподвижной оси, а также при плоскопараллельном движении (вращении вокруг мгновенного центра скоростей) элементарная работа определяется по формуле
Аk МО(Fk ) k ,
где MО(Fk ) – момент силы относительно оси вращения, проходящей через
точку О; δφk – возможное угловое перемещение.
Элементарная работа положительна, когда направления момента и возможного углового перемещения совпадают, и отрицательна, когда они противоположны. Если в состав системы входят тела, совершающие поступательное, вращательное и плоскопараллельное движения, уравнение
(10.8) можно представ ть в виде |
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
s |
|
|
s ) |
n |
|
|
0 . |
(10.11) |
|
F |
k |
cos(F , |
M |
0 |
F |
k |
|
k 1 |
k |
|
|
k |
k |
k 1 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
План решен я |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1. |
ть все |
|
задаваемые |
силы |
и |
|
показать |
моменты |
задачи |
|
|
|
|
|
|
|
|
|
|
действующ х пар с л. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Сообщ ть с стеме возможное перемещение и показать на рисунке |
углы δφk |
элементарных |
|
поворотов |
тел |
и векторы |
sk элементарных |
перемещенийИзобразточек приложения сил.
3. Подсчитать элементарные работы всех активных сил на заданном возможном перемещении и составить уравнение (10.11).
4. Выразить все величины δsk, δφk через какую-либо одну, для чего
|
следует установить зависимость между δsk и δφk, учитывая, что модуль |
|
|
А |
|
вектора sk |
|
вычисляется как длина дуги по формуле sk rk δφk. |
|
|
Д |
После замены величин sk , δφk через одну из полученного уравнения можно определить искомую силу, или искомый момент пары сил, или
искомую зависимость между действующими силами и моментами пар сил. |
|
|
|
|
k |
|
|
|
И |
10.6.2. Кинематический метод |
При использовании кинематического метода учитываются связи |
между возможными |
скоростями Vk точек приложения сил и их |
возможными перемещениями s |
|
, а также между угловыми скоростями ωk |
звеньев, к которым приложены силы, и их возможными угловыми |
перемещениями δφk : V |
|
sk |
; |
k |
|
k |
. |
|
|
|
k |
|
dt |
|
|
dt |
При этом показывают не возможные перемещения, а возможные скорости точек приложения сил и возможные угловые скорости звеньев, к которым приложены силы. Принцип возможных перемещений
10.6.3. Аналитический метод
превращается в принцип возможных скоростей и расчетная формула (10.11) принимает вид
n |
|
|
|
n |
|
|
|
|
0 . |
(10.12) |
F V |
cos(F ,V ) M |
|
F |
|
k 1 |
k k |
k |
k |
k 1 |
0 |
k |
|
k |
|
|
равнение показывает полную аналогию структур построения формул
(10.11) и (10.12).
Анал т ческ й метод позволяет формализовать процесс решения |
проекции |
|
|
|
задачи. Он заключается в определении работ задаваемых сил на |
Свозможном перемещен |
системы через |
проекции сил и |
проекции |
возможных перемещен й на декартовы оси координат: |
|
|
|
б |
|
|
|
|
|
n |
|
|
|
(10.13) |
|
|
|
Fkx xk Fky yk Fkz zk 0 , |
|
|
|
k 1 |
|
|
|
|
здесь |
Fkx , Fky , Fkz – |
|
k-й силы; |
δxk , δyk , δzk – |
проекции |
возможного перемещен я sk точки приложения этой силы на оси. |
Проекц |
А |
|
возможных |
перемещений |
вычисляют путем записи |
уравнений координат для точек приложения сил и применения к этим |
уравнениям |
|
операции |
варьирования |
(аналогичной |
операции |
дифференцирования функции). |
|
|
|
План решения задачи. |
|
|
|
|
1. |
Показать все задаваемые силы и моменты действующих пар сил. |
2. |
Выбрать неподвижную систему декартовых координат, связав ее с |
телом, которое при возможном перемещении системы остается |
неподвижным. |
|
|
|
|
|
3. |
Вычислить проекции заданных сил на оси Fkx , Fky , Fkz . |
|
4. |
|
|
|
|
|
И |
Записать уравнения координат точек приложения сил xk, yk, zk. |
5. |
Найти значения δxk , δyk ,Дδzk дифференцированием уравнений |
координат по выбранному обобщенному параметру. |
|
6. |
Записать уравнение возможных работ в виде (10.13). |
|
7. |
Определить искомый параметр. |
|
|




