
2192
.pdf3.4. Три формы записи уравнений равновесия плоской системы сил
Получены общие уравнения равновесия плоской системы сил, действующих на твердое тело, в следующей форме:
n |
0 ; |
n |
0 ; |
n |
М |
|
|
(3.10) |
F |
F |
|
|
(F ) 0. |
||||
i 1 ix |
|
i 1 iy |
|
i 1 |
|
O |
i |
|
С |
|
|
|
|
|
|
|
|
Уравнения (3.10) называют уравнениями равновесия плоской системы |
||||||||
сил в первой форме. |
|
|
|
|
|
|
|
|
Уравнен я равновесия плоской системы сил, приложенных к
твердому телу, можно записывать в других эквивалентных формах. |
|
||||||||||
иначе |
|
|
|
|
|
|
|||||
Уравнен я равновес я плоской системы сил можно сформулировать |
|||||||||||
: для равновес я плоской системы сил, приложенных к твердому |
|||||||||||
телу, необход |
мо |
достаточно, |
чтобы суммы алгебраических моментов |
||||||||
сил относ тельно двух лю ых точек и алгебраическая сумма проекций |
|||||||||||
этих с л на ось плоскости, не перпендикулярную прямой, проходящей |
|||||||||||
через две моментные точки, |
ыли равны нулю, т.е. |
|
|
||||||||
n |
|
|
|
|
n |
|
|
|
n |
|
|
|
М |
|
(F ) 0 ; |
М |
|
(F ) 0 ; |
F |
0 , |
(3.11) |
||
i 1 |
|
А |
|
i |
i 1 |
|
В |
i |
i 1 iх |
|
|
где за ось Оx пр нята лю ая прямая, не перпендикулярная АВ. |
|
||||||||||
|
|
|
|
А |
|
||||||
Уравнения (3.11) представляют вторую форму записи уравнений |
|||||||||||
равновесия бплоской произвольной системы сил. |
|
|
|||||||||
Возможна третья форма записи уравнений равновесия. |
|
||||||||||
Для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю, т.е.
n |
|
|
|
n |
|
|
|
n |
М |
|
|
(3.12) |
М |
|
(F ) 0 ; |
М |
|
(F ) 0 ; |
|
|
(F ) 0. |
||||
i 1 |
А |
|
i |
i 1 |
В |
|
i |
i 1 |
|
С |
i |
|
Точки А, В, С не должны лежать на одной прямой. |
|
|||||||||||
Уравнения |
(3.12) |
являются |
Дтретьей формой записи уравнений |
|||||||||
равновесия плоской произвольной системы сил. |
|
|
|
|
||||||||
В частном случае плоской системы параллельных сил можно сформулировать другую форму уравнений равновесия этой системы сил:
для равновесия плоской системы параллельных сил, приложенных к
твердому телу, необходимо и достаточно, |
чтобы суммы алгебраических |
|||||||
|
|
|
|
|
|
|
И |
|
моментов сил относительно двух любых точек были равны нулю, т.е. |
||||||||
n |
М |
|
|
n |
М |
|
|
(3.13) |
|
|
(F ) 0 ; |
|
|
(F ) 0 . |
|||
i 1 |
|
А |
i |
i 1 |
|
В |
i |
|
Точки А и В нельзя брать на прямой линии, параллельной силам
161
3.5. Определение реакций опор механической системы
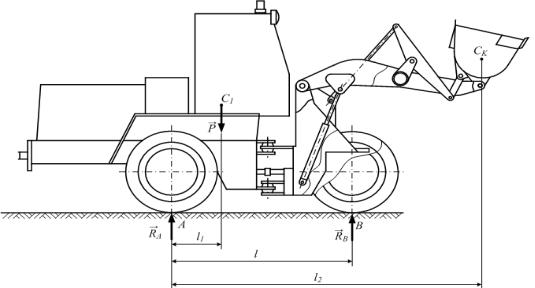
Погрузочно-транспортная машина с грузом в ковше с позиций теоретической механики представляет собой твердое тело, имеющее силу
тяжести P , приложенную в точке С1 (рис. 3.5). Cила P является равнодействующей системы параллельных сил всех тел механической
системы, |
а точка 1 является точкой приложения равнодействующей. Для |
|
превращения несвободного твердого тела в свободное необходимо |
||
освобод |
ть его от связей. В данном случае связью является горизонтальная |
|
поверхность. Поэтому реакции опорной поверхности RA и RB тоже |
||
являются |
|
силами. |
С |
|
|
параллельными |
||
|
б |
|
|
|
АРис. 3.5 |
Таким образом, рассматриваемое твердое тело находится в равновесии под действием силы тяжести P и двух реакций RA , RB . Для
системы параллельных сил опорную реакцию |
RA определим из уравнения |
|||
Д |
||||
моментов сил относительно точки В: |
|
|
|
|
n |
|
P(l l1) |
|
|
M iB 0 ; P(l l1) RA l 0 , откуда RA |
. |
|||
|
||||
i 1 |
|
l |
||
Реакцию RB определим из уравнения проекций сил на вертикальную |
||||
ось |
И |
|||
n |
||||
Fiy 0 ; P RA RB 0 ; |
RB P RA . |
|||
i 1
162
3.6. Приведение пространственной системы параллельных сил
Пространственная |
|
|
|
система |
|||||
параллельных сил не приводится к динаме, |
|||||||||
так как для нее главный вектор и главный |
|||||||||
момент |
в |
общем |
случае |
|
взаимно |
||||
С |
|
|
|
|
|
|
|
||
перпендикулярны. Для доказательства этого |
|||||||||
рассмотрим |
пространственную |
|
систему |
||||||
параллельных с л, для которой главный |
|||||||||
вектор |
главный момент не равны нулю. |
|
|
||||||
координат |
|
|
|
|
|||||
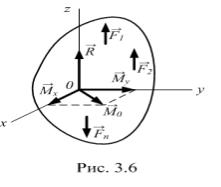
Выберем за центр приведения точку О – начало декартовой системы |
|||||||||
|
, ось Оz которой направим параллельно силам (рис. 3.6). Тогда |
||||||||
проекц |
главного вектора на оси координат Ox, Oy являются тождествами |
||||||||
|
б |
|
n |
||||||
|
|
|
Rx |
n |
|
|
|
|
|
|
|
|
Fix 0 ; |
Ry Fiy 0, |
|||||
|
|
|
|
i 1 |
|
|
|
i 1 |
|
так как параллельные силы перпендикулярны этим осям. Проекция |
|||||||||
главного вектора на ось Оz |
в о щем случае не равна нулю. Она равна |
||||||||
|
|
|
А |
||||||
алгебраической сумме параллельных сил, т.е. |
|||||||||
|
|
|
|
Rz |
n |
|
n |
|
|
|
|
|
|
Fiz |
Fi |
0. |
|||
|
|
|
|
|
i n |
|
i 1 |
|
|
Следовательно, |
главный вектор |
R параллелен оси Оz. Для проекций |
|||||||
|
|
|
|
|
|
Д |
|||
главного момента на оси координат имеем |
|
|
|||||||
n |
Мх(Fi ) 0 ; |
|
n |
|
|
|
|
n |
|
Мx |
Мy Му(Fi ) 0; |
|
Мz Мz (Fi ) 0 . |
||||||
i 1 |
|
|
|
i 1 |
|
|
|
i n |
|
Проекция главного момента на ось Оz |
равна нулю, так как каждая |
||||||||
сила параллельна этой оси. |
|
|
|
|
И |
||||
|
|
|
|
|
|||||
Таким образом, главный момент расположен в плоскости Оxy, перпендикулярной главному вектору, направленному по оси Оz. В этом
случае система сил приводится к равнодействующей. |
|
|
|
|||||||
Для |
системы |
параллельных сил |
имеем другие |
частные |
случаи |
|||||
|
|
|
; |
|
0 0 |
– система |
приводится |
к |
паре сил; |
|
приведения: R 0 |
M |
R 0 ; |
||||||||
|
или |
|
|
|
0 – |
система приводится к |
равнодействующей |
|||
M 0 0 |
R 0 ; |
M 0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
силе; R |
0 ; |
M 0 |
0 – имеем уравновешенную систему сил. |
|
||||||
163
3.7.Равновесие твердого тела
3.7.1.Равновесие тела с двумя закрепленными точками
Твердое тело с двумя опорами в точках А и
В имеет неподвижную ось вращения, |
||||||||
проходящую через эти точки. Пусть тело |
||||||||
С |
|
|
|
|
|
|||
находится в равновесии под действием |
||||||||
приложенных сил (F1, F2 ,...., Fn ) . Освободим |
||||||||
тело от связей, пр лож в в опорах А и В силы |
||||||||
реакции |
RA |
RB . |
Эти |
силы разложим |
на |
|||
уравнений |
координат |
|||||||
составляющ е, параллельные осям |
||||||||
|
|
|
|
|
|
|
|
|
X A , |
YA , |
Z A |
X B , |
YB , |
для сво одного тела |
|||
можем состав ть 6 |
|
равновесия сил. |
|
|||||
|
|
б |
|
|
||||
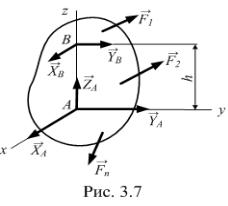
|
Обознач в АВ через h (рис. 3.7), |
получим |
||||||
|
|
|
n |
|
X B 0 ; |
|
n |
|
|
|
|
Fix X A |
|
M x (Fi ) YBh 0 ; |
|||
|
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
n |
|
|
|
n |
|
|
|
|
Fiy YA |
YB 0 ; |
|
M y (Fi ) X B h 0; |
||
|
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
n |
|
|
|
n |
|
|
|
|
Fiz Z A |
0 ; |
|
M z (Fi ) 0 . |
||
|
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
Д |
|||
|
Имеем для тела 6 уравнений равновесия и 5 неизвестных величин. |
|||||||
Одно из полученныхАуравнений является условием вращения тела. В |
||||||||
рассматриваемом случае тело имеет одну степень свободы, оно может |
||||||||
вращаться вокруг оси Оz (ось В). Приложенные силы удовлетворяют |
||||||||
одному условию равновесия. Сумма моментов заданных сил относительно |
||||||||
оси Оz обращается в нуль. |
|
|
|
|
||||
|
|
|
3.7.2. Твердое тело с одной закрепленной точкой |
|||||
|
Тело с одной закрепленной точкой имеет три степени свободы. Оно, |
|||||||
например, может вращаться вокруг каждой из трех осей координат, |
||||||||
проходящих через закрепленную точку. |
|
И |
||||||
164

Если твердое тело с одной |
|
|
|
||||||
закрепленной точкой А, принимаемой за |
|
|
|
||||||
шаровой |
шарнир, |
освободить |
от |
этой |
|
|
|
||
связи, то для составляющих сил реакций |
|
|
|
||||||
связи X A |
, YA , Z A и приложенных к телу |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
сил (F1 |
, F2 ,...., Fn ) |
можно |
составить |
|
|
|
|||
следующие шесть уравнений (рис. 3.8): |
|
|
|
|
|||||
С |
n |
X A |
|
|
n |
|
|
||
Fix |
0 ; |
|
M x (Fi ) 0; |
||||||
|
|
i 1 |
|
|
|
|
i 1 |
|
|
|
|
n |
YA |
|
|
n |
|
||
|
|
Fiy |
0 ; |
|
M y (Fi ) 0 ; |
||||
|
б |
i 1 |
|
|
|||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
n |
Z |
|
0 ; |
|
n |
|
|
|
|
F |
A |
|
M |
z |
(F ) 0 . |
||
иiz |
|
|
i 1 |
i |
|||||
|
|
i 1 |
|
|
|
|
|
|
|
В этом случае имеем три уравнения равновесия с тремя неизвестными и три условияАравновесия. Задача статически определима. Приложенные силы удовлетворяют трем условиям равновесия, т.е. равны нулю суммы моментов приложенных сил относительно каждой из трех осей координат. В эти условия не входят неизвестные силы реакций. В рассмотренном случае число условий равновесия, совпало с числом степеней свободы этого тела. Для Дсвободного твердого тела имеем шесть степеней свободы и соответственно шесть условий равновесия сил.
И
165
КИНЕМАТИКА
ИСХОДНЫЕ ПОЛОЖЕНИЯ, ОСНОВНЫЕ РАЗДЕЛЫ
|
Материальная точка может рассматриваться как модель твердого |
||||||
тела, совершающего поступательные движения, когда размеры твердого |
|||||||
С |
|
|
|
|
|
||
тела не имеют существенного значения. |
|
||||||
В |
разделе |
«Кинематика» |
|
изучают |
|
||
движен я точек, тел и механических |
|
||||||
систем в заданных с стемах координат; |
|
||||||
характер ст ки |
механ ческого |
движения |
|
||||
материальных |
точек |
тел, |
которыми |
|
|||
являются траектор |
, |
, |
ускорения |
|
|||
и |
методы х |
определения при |
разных |
|
|||
|
б |
|
|||||
случаях задан я дв |
жен |
я. |
|
|
|
||
|
Дв жен е матер альных о ъектов рассматривают в плоскости или |
||||||
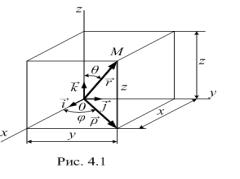
пространствескорости; спользуют эвклидово трехмерное пространство и |
|||||||
различные с стемы координат: правую декартову прямоугольную систему |
|||||||
координат Oxyz (р с. 41.1), цилиндрическую систему координат ρ, φ, z и |
|||||||
|
|
|
ТИКА |
|
|||
сферическую систему координат |
r, |
θ, φ (радиус-вектор, широта и долгота), |
|||||
полярную систему координат ρ, φ в плоскости, а также другие системы |
|||||||
координат. Основными разделами кинематики являются: кинематика |
|||||||
точки, твердого тела и механической системы. |
|
||||||
|
|
|
|
|
|
Д |
|
|
|
|
|
4. КИНЕМ |
ТОЧКИ |
|
|
|
|
4.1. Способы задания движения точки |
|
||||
|
Движение |
точки |
считают заданным, если в выбранной |
системе |
|||
|
|
|
|
|
|
И |
|
отсчета можно определить положение точки в любой момент времени. |
|||||||
Движение точки можно задавать разными способами. Рассмотрим |
|||||||
основные из них. |
|
|
|
|
|
||
|
4.1.1. Векторный способ задания движения точки |
|
|||||
|
При векторном способе задания движения положение точки на |
||||||
траектории определяют концом радиуса-вектора r , проведенного из |
|||||||
некоторой неподвижной точки О: |
r r( t ) . |
(4.1) |
|||||
|
|
|
|
|
|
||
Векторное уравнение (4.1) представляет собой уравнение движения точки. Точка движется по траектории, которая задана концом радиуса-
166
вектора. Уравнение (4.1) можно записать в проекциях на декартовы оси координат Ox, Oy, Oz
r i х jy kz, |
(4.2) |
где i , j ,k – единичные векторы-орты координатных осей.
4.1.2. Координатный способ задания движения точки
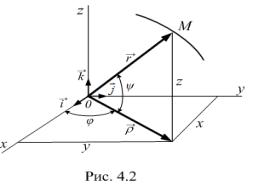
Дв жен е точки задают в декартовой системе координат путем задания коорд нат точки в виде скалярных функций времени (рис. 4.2)
х=f1(t); |
у= f2(t); z= f3(t). |
(4.3) |
|
СУравнен я (4.3) представляют |
|||
собой уравнен я дв жения точки в |
|||
декартовой |
|
прямоугольной |
системе |
координат, они позволяют для каждого |
|||
момента времени указать положение |
|||
точкив выбранной с стеме Oxyz. |
|||
Поэтому уравнен я (4.3) являются также и уравнениями траектории |
|||
|
|
А |
|
точки, заданными параметрически. Для получения явного вида уравнения |
|||
траектории бследует получить уравнение f(х,у,z)=0, в котором отсутствует |
|||
время t. Уравнение (4.2) связывает векторный и координатный способы |
|||
задания движения точки. |
Д |
||
Пример 1. |
|
||
Движение точки задано в векторной форме уравнением |
|||
|
|
r (2t 3)i t 2 j 4 k . |
|
Записать уравнения движения точки в координатной форме.
Решение.
В соответствии с формулой (4.2) х=2t – 3; y= – t2; z=4.
Уравнение (4.2) позволяет также перейти от координатного способа задания движения точки к векторному.
Пример 2. Движение точки в плоскости Оxy задано уравнениями x=2t; y=8t2.
Определить траекторию точки, начало и направление движения. |
||
Решение. Исключим из уравнения движения параметр t. з первого |
||
уравнения находим t |
x |
И |
|
и, подставляя это значение t во второе уравнение, |
|
2 |
|
|
получаем y=2x2. |
|
|
167
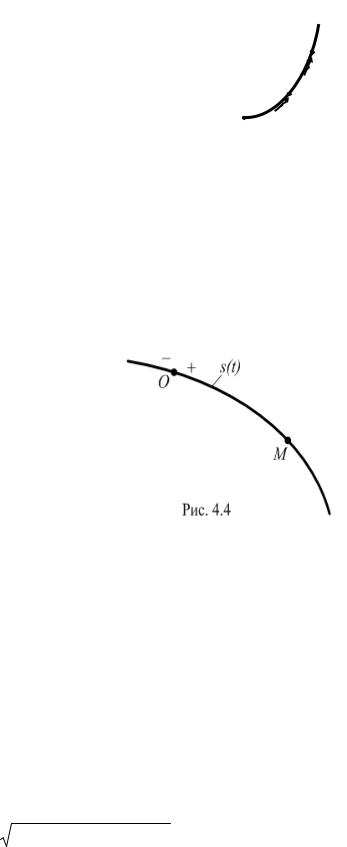
Следовательно, получено уравнение параболы с |
|
|
|
|
||||||
|
|
|
||||||||
вершиной в начале координат и осью, совпадающей с |
|
|
|
|
||||||
осью Оy (рис. 4.3). В начальный момент времени t0=0 |
|
|
|
|
||||||
координаты точки x0=0; y0=0. Следовательно, точка |
|
|
|
|
||||||
начинает движение из начала координат. При любом |
|
|
|
|
||||||
значении времени t координаты точки x и y будут |
|
|
|
|
||||||
С |
|
|
|
|
|
|
|
|
||
положительными, поэтому траекторией будет не вся |
|
|
|
|
|
|||||
парабола, а только правая её ветвь. |
|
|
|
|
|
|
||||
отсчитываетсяДля задан уравнен я движения точки |
|
|
||||||||
|
4.1.3. Естественный способ задания движения точки |
|
|
|||||||
Пусть точка дв жется |
по заданной криволинейной траектории. При |
|||||||||
естественном спосо |
задания движения точки задают: траекторию точки; |
|||||||||
начало |
направлен е |
отсчёта дуговой координаты s, которая |
||||||||
|
|
начала отсчета. |
|
|
|
|
|
|
||
по траектор |
нео ходимо вы рать |
на |
|
|
||||||
заданной траектор |
точку О, принимаемую |
|
|
|||||||
|
|
|
А |
|
|
|||||
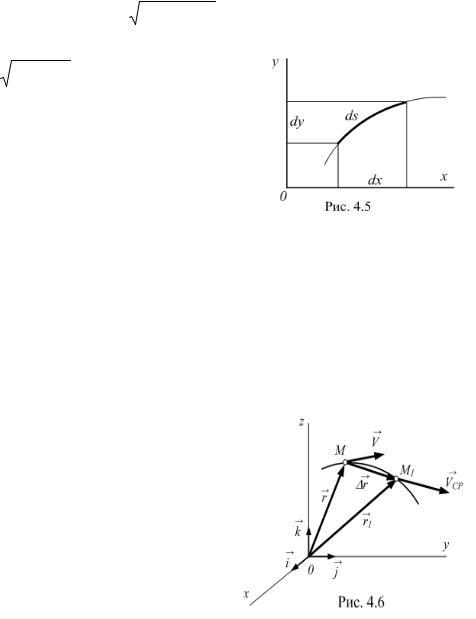
за начало отсчёта дуговой координаты (рис. |
|
|
||||||||
4.4). Обычнобза t=0 принимают момент |
|
|
||||||||
времени, когда движущаяся точка проходит |
|
|
||||||||
через точку О. Дуговая координата |
|
|
||||||||
рассматривается |
|
как |
координата, |
|
|
|||||
отсчитываемая |
|
по |
Д |
|
|
|||||
|
криволинейной |
|
|
|||||||
траектории. Зависимость |
s s(t) |
|
|
|
|
(4.4) |
||||
является уравнением движения точки по траектории.
Необходимо отметить, что величина s в уравнении (4.4) определяет дуговую координату (положение) на траекторииИдвижущейся точки, а не пройденный ею путь. Например, точка, совершая колебательное движение вдоль траектории относительно точки О, окажется в итоге в положении М. Пройденный за время движения путь σ не равен дуговой координате s. Эти параметры будут совпадать только в том случае, когда точка движется в направлении отсчёта дуговой координаты. Покажем связь между координатным и естественным способами задания движения точки. Известно, что элемент дуги ds связан с координатами движущейся точки следующим уравнением:
ds (dx)2 (dy)2 (dz)2 .
Интегрируя это уравнение, получим уравнение движения точки
168
|
|
|
|
|
|
|
|
|
|
s(t) t |
Vdt , |
|
|
(4.5) |
||
где V – скорость точки. |
|
|
0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
Здесь s(0) 0; |
|
dx xdt; |
dy ydt; |
|
dz zdt. |
|
|||||||||
|
Если точка движется в плоскости Oxy, то уравнение движения точки |
|||||||||||||||
выражается, согласно теореме Пифагора (рис. 4.5), |
||||||||||||||||
|
|
|
|
|
|
|
|
|
ds |
dx2 dy2 , |
|
|
(4.6) |
|||
и после |
нтегр рован я – в конечной форме |
|
|
|
||||||||||||
|
|
|
|
t |
|
2 |
|
2 |
|
t |
|
|
|
|
|
|
|
|
|
(t) |
0 |
|
|
dt |
0 Vdt. |
|
|
(4.7) |
|
||||
|
|
|
x |
|
y |
|
|
|
||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
прямол нейном движении точки путь |
|
||||||||||||
будет выч сляться по формуле |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vdt. |
|
|
|
(4.8) |
|
|||
|
|
|
|
(t) xdt |
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
При |
|
|
|
|
|
|
||||||||||
|
|
|
4.2. Скорость |
|
ускорение точки при векторном способе |
|||||||||||
|
|
|
|
|
|
|
|
|
задания движения |
|
||||||
|
|
|
б |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
4.2.1.Скорость точки |
|
|
|||||
|
|
Одной из основных характеристик движения точки является её |
||||||||||||||
скорость относительно выбранной системы отсчёта, которая изображена в |
||||||||||||||||
|
|
|
|
|
|
|
А |
|||||||||
виде декартовой прямоугольной системы координат (рис. 4.6). |
||||||||||||||||
|
Положение движущейся точки М в |
|
|
|||||||||||||
рассматриваемой |
|
|
|
системе |
отсчёта |
|
|
|||||||||
определяется в момент времени t |
радиусом- |
|
|
|||||||||||||
вектором |
r , |
|
|
который |
соединяет |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||
неподвижную точку О с этой точкой. В |
И |
|||||||||||||||
другой |
момент |
|
|
времени |
t1 t t |
|||||||||||
движущаяся точка займёт положение M1 и её |
||||||||||||||||
радиусом-вектором будет r1 . За время ∆t |
||||||||||||||||
радиус-вектор движущейся точки изменится |
||||||||||||||||
на r |
r1 r. |
|
|
|
|
|
Vср |
|
|
|
|
|
||||
|
Средней |
скоростью |
точки за |
время |
|
∆t называют отношение |
||||||||||
V |
|
r |
. Средняя скорость совпадает с вектором r . В общем случае она |
|||||||||||||
ср |
|
t |
|
|
|
|
|
осреднения ∆t. |
|
|
|
|
|
|||
зависит |
от времени |
|
Введём |
|
понятие действительной |
|||||||||||
169
скорости точки V в момент времени t, которая определяется как предел средней скорости, если промежуток времени, за который определяется
средняя скорость, стремится к нулю, т.е. V lim |
r |
dr . |
t 0 |
t |
dt |
Таким образом, скорость точки равна первой производной по времени от |
||
Сеё радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки. Для характеристики переменного вектора используют понятие его годографа.
конца вектора, если переменный вектор в различные моменты времени
откладывать от одной той же общей точки.
радиусаразличные-вектора r (р с. 4.6). Последовательные положения вектора r в моменты времени откладываются в этом случае от точки О.
огласно определению, траектория точки является годографом
Первая про зводная по времени от радиуса-вектора есть скорость точки, направленнаябпо касательной к траектории, т. е. к годографу радиуса-вектора.
А
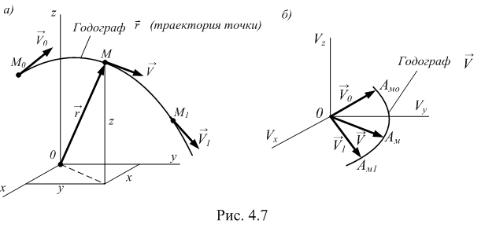
Годографом вектора скорости является линия, на которой располагаются концы вектора скорости в различные моменты времени,
если их начала совместить в одной общей точке (рис. 4.7). |
|
Для |
построения годографа Двектора скорости выбирают точку, |
например О (рис. 4.7,б), и начала векторов скорости для различных |
|
моментов времени помещают в эту точку, не изменяя их направлений. |
|
Каждой точке М траектории (рис. 4.7,а) соответствует своя изображающая |
|
точка АМ |
на годографе вектора скорости (см. рис. 4.7,б). Масштаб |
скоростей при построении годографа вектора скоростиИможет быть выбран |
|
отличным от масштаба для скоростей, изображаемых в точках траектории. |
|
При движении точки М по траектории соответствующая ей изображающая |
|
точка АМi |
движется по годографу вектора скорости. |
При равномерном движении точки по прямой годографом вектора скорости является одна точка, при неравномерном движении – отрезок этой прямой.
170
