
2192
.pdfНьютона и расчетной схемой (см. рис. 7.2,а), когда система двух тел рассматривается как единая механическая система, со вторым телом которой связана неподвижная система координат.
В уравнении принципа Даламбера для несвободной материальной
точки левая часть уравнения (9.3) представляет собой силу инерции Ф, которая является силой реакции отброшенной гравитационной части
механической системы. Заменяя силу инерции Ф произведением массы на ускорение точки, получаем основное уравнение динамики (9.1). Таким образом, в случае д намики несвободной материальной точки основное уравнен е д нам ки (9.1) и уравнение Даламбера (9.3) равноценны. В
рассмотренном случае в задачах движения материальной точки |
|||||||||||||
использован е понят я «сила инерции» не дает ничего нового, |
|||||||||||||
С |
|
|
|
|
|
|
|
|
|||||
т.к.про сход т математ ческая замена силы инерции произведением |
|||||||||||||
массы на ускорен е. В задачах определения сил реакций связей сила |
|||||||||||||
инерции |
|
спользуется как реальная сила наряду с другими действующими |
|||||||||||
силами |
наход тся в согласии с принципом независимого действия сил. |
||||||||||||
|
|
Даламбера, положенные в основу создания уравнений движения |
|||||||||||
Идеи |
|
|
|
|
|
|
|||||||
несвободной матер альной точки и механической системы, оказались |
|||||||||||||
плодотворными |
непрерывно развивались в течение последних столетий. |
||||||||||||
В учебной и технической литературе бытует мнение о том, что основное |
|||||||||||||
уравнение |
динамики |
Ньютона |
для |
решения |
задач |
динамики |
|||||||
|
|
|
|
удобно |
|
|
|
|
|
||||
материальной точки, а принцип Даламбера – для решения задач динамики |
|||||||||||||
сложных механических систем. |
|
|
|
|
|
|
|||||||
|
|
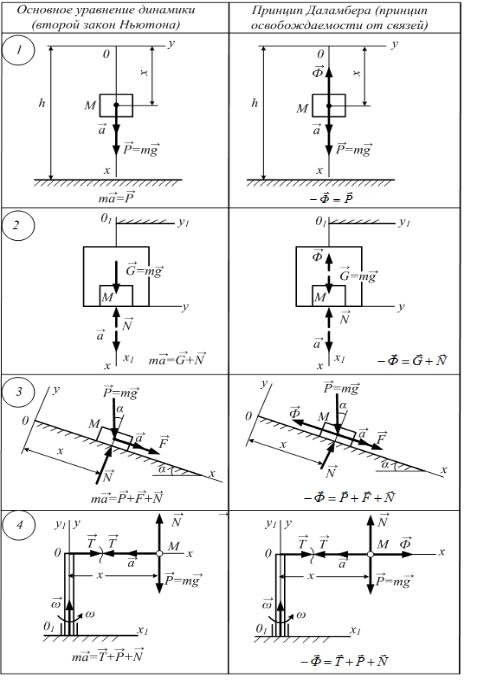
На рис. 9.2 показаны расчётные схемы для решения различных задач |
|||||||||||
динамики |
точки |
одновременно |
при помощи основного |
уравнения |
|||||||||
|
|
|
|
|
|
А |
|
|
|
||||
динамики точки и принципа Даламбера. |
|
|
|
|
|
||||||||
|
|
|
|
9.2.1. Свободное падение материальной точки |
|
|
|||||||
|
|
|
|
|
|
|
у поверхности Земли |
|
|
|
|
||
|
|
|
|
|
|
|
|
Д |
|||||
|
|
Точка массой m падает с высоты h. В начале падения при t=0 x0 0 ; |
|||||||||||
|
|
|
|
|
|
|
|
( ) |
|
|
|||
x0 |
|
0 . |
Определить |
уравнение |
скорости |
точки x t |
|
и |
уравнение |
||||
|
|
|
|
|
|
( ) |
, принимая в пределах ограниченного изменения |
||||||
перемещения точки x t |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
И |
|||
высоты h ускорение g постоянным (рис. 9.2,1). Для соответствующих задач слева показаны расчетные схемы по Ньютону, а справа – по Даламберу для материальной точки. Отличие этих схем состоит в том, что левые расчетные схемы содержат активные силы, приложенные к точке. При этом равнодействующая этих сил совпадает с направлением ускорения точки.
221
С |
|
и |
|
б |
|
А |
|
Д |
|
Рис. 9.2 |
И |
|
|
В даламберовых схемах показаны действующие силы и реакции связей, а также сила инерции, которая является мерой противодействия
активным силам при движении точки.
Сила инерции пропорциональна массе, при этом коэффициентом
пропорциональности является ускорение Ф ma .
Кеплер считал, что сила инерции есть сила сопротивления всякому изменению состояния движения. Аналогичных суждений придерживались Ньютон, Даламбер и другие.
222
Несмотря на различные исходные расчетные схемы и различные векторные уравнения для решения задачи, последующие проекции этих уравнений на координатную ось х дают эквивалентные дифференциальные уравнения. Для свободно падающего тела (см. рис.9.2,1) имеем для левой и правой расчетных схем
|
|
|
|
|
|
|
t |
2 |
|
|
a g ; |
dx |
g ; |
C1 ; x g |
|
C1t C2 . |
|
||||
mx |
mg ; x |
dt |
x gt |
2 |
|
|||||
Из начальных условий находим С1=0; |
С2=0. |
|
|
|
|
|||||
Получен од наковый результат решения задачи при разных исходных |
||||||||||
начальных уравнен ях разными способами. |
постоянным |
ускорением |
a , |
|||||||
произведенВ каб не л фта, опускающейся с |
||||||||||
В рассмотренной задаче сила инерции Ф математически заменяется |
||||||||||
Сем массы тела на ускорение и никаких дополнительных сил, |
||||||||||
действующ х на точку, не появляется. |
|
|
|
|
|
|||||
|
б |
|
|
|
|
|
||||
|
|
9.2.2. Опускание кабины лифта |
|
|
|
|
||||
определ ть с лу нормального давления N тела M на основание лифта
(рис. 9.2,2). Масса тела m, начальные условия следующие: при t=0 x0 0 ; |
||||
x0 0 . Векторные уравнения динамики, по Ньютону и Даламберу, имеют |
||||
|
|
|
|
|
различную математическую форму записи и разное физическое |
||||
содержание. |
|
|
|
|
|
При помощи основного уравнения динамики получаем |
|||
|
|
mx mg N ; ma |
Д |
|
|
|
mg N ; |
N mg ma . |
|
|
|
|
|
|
|
С помощью принципаАДаламбера запишем уравнение проекций сил на |
|||
ось x: |
X i Ф mg N 0 ; |
N mg Ф. |
||
|
Полученные результаты показывают, что в рассмотренной задаче в |
|||
основном уравнении динамики и в принципе аламбера сила инерции Ф |
||||
|
|
|
|
И |
является реальной силой, т.к. нормальная сила равна разности сил тяжести |
||||
и инерции. |
|
|
|
|
|
При N=0 получаем явление невесомости, при котором сила тяжести |
|||
G |
уравновешена силой инерции Ф. Сила инерции Ф в данном примере |
|||
является силой противодействия приложенным силам G N . |
||||
|
9.2.3. Движение тела по наклонной плоскости под действием силы, |
|||
|
|
пропорциональной времени |
||
|
Тело движется по гладкой наклонной плоскости. Сила F kt , угол |
|||
наклонной плоскости ; при t=0 |
x0 0 ; |
x0 0 . Определить уравнения |
||
|
|
|
|
|
скорости и перемещения тела по гладкой наклонной плоскости.
223
Основное уравнение динамики Ньютона и векторное уравнение принципа Даламбера для несвободной материальной точки представлены на рис. 9.2,3. Дифференциальные уравнения движения для обоих случаев являются одинаковыми:
С |
mx mg sin kt ; x g sin m t ; |
|
||||||||
|
|
|
|
|
|
|
k |
|
||
k t 2 |
t 2 |
|
k t3 |
|
||||||
|
С1; x g sin |
|
С1t C2 . |
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
||||
x g sin t |
m 2 |
2 |
m 6 |
|||||||
|
|
|
|
|
||||||
В данном случае с ла инерции Ф является силой противодействия |
||||||||||
силам P F N . |
|
|
|
|
|
|
|
|
|
|
горизонтальной |
|
|
|
|
|
|
||||
9.2.4. Вращение тела в горизонтальной плоскости |
||||||||||
Тело массой m, пр нимаемое за материальную точку М, вращается в |
||||||||||
б |
|
|
|
|
|
|
||||
плоскости вокруг вертикальной оси на стержне длиной |
||||||||||
х=r с постоянной угловой скоростью (рис. 9.2,4).
Определ ть ус л е в стержне и дать характеристику движения тела. В данном случае точка М совершает вращательное движение, поэтому
для пр менен я пр Анципа осво ождаемости от связей необходимо мысленно прекратить вращение системы, зафиксировать ее параметры, применить к точке принцип осво ождаемости от связей, с помощью которого внутренние силы реакции системы переводятся в разряд внешних сил, действующих на точку.
На рис. 9.2,4 показаны силы, действующие на точку М с использованием принципа освобождаемости от связей, и приведены векторные уравнения движения точки для основного уравнения динамики Ньютона и принципа Даламбера. Усилие в стержне Т, согласно принципу
Даламбера, равно силе инерции Ф. |
В данной задаче сила инерции Ф |
|||
|
|
|
И |
|
является реальной единственной действующей силой, создающей |
||||
динамическую силу реакции Т в Дстержне. По Ньютону, mx T ; |
по |
|||
Даламберу, Ф T . |
|
|
|
|
|
T mr 2 ; |
Т=Ф. |
|
|
При условии const сила инерции Ф и реакция связи Т находятся в |
||||
стационарном равновесии. |
|
|
|
|
9.2.5. Равновесие математического маятника при вращении |
|
|||
Маятник и кронштейн вращаются с угловой скоростью |
|
|||
(рис. 9.3,1). Маятник находится в относительном покое в неинерциальной системе координат Оху.
224

Согласно принципу Даламбера, силы, действующие на маятник,
находятся в стационарном равновесии: Ф N P . |
Решаем уравнения |
||
равновесия: |
|
|
|
Xi 0; |
Ф N sin ; Yi 0; P N cos . Откуда Ф P tg . |
||
При отсутствии вращения маятник находится в отвесном положении: |
|||
0; 0. |
|
|
|
В общем случае сила инерции Фобеспечивает равновесие маятника |
|||
(рис. 9.3,1) |
|
|
|
С |
Ф m 2 (l OM sin ) . |
(9.5) |
|
|
|
||
9.3. Пр нц п Даламбера для системы материальных точек |
|||
Рассмотр |
с стему из n материальных точек. |
В каждой точке |
|
системы в общем случае приложены равнодействующая активных сил Fk |
|
и равнодействующая реакций связей Rk . Применяя принцип Даламбера к |
|
каждойполучимточке с стемы, |
|
Fk Rk Фk 0 , |
(9.6) |
где Фk mk ak – сила инерции k-й точки.
Векторные уравнения (9.6) выражают сущность принципа Даламбера: |
||||||
|
б |
|
|
|||
при движении механической системы активная сила и реакция связи вместе с |
||||||
силой инерции образуют уравновешенную систему сил для каждой точки |
||||||
системы. |
А |
|
||||
|
|
|
|
|
|
|
Принцип Даламбера для системы |
|
|
|
|||
по своему содержанию не отличается |
|
|
|
|||
от уравнений движения всех её точек. |
|
|
|
|||
Представим равнодействующую |
силу, |
|
|
|
||
приложенную к каждой точке системы, |
|
|
|
|||
разложенную не на активную силу и |
|
|
|
|||
реакцию связей, а на внутреннююДи |
|
|||||
внешнюю силы по отношению ко всей |
|
|
|
|||
системе (рис. 9.3): |
|
|
|
Рис. 9.3 |
|
|
|
F R |
F e F i . |
|
|||
|
k |
k |
k |
k |
|
|
Тогда принцип Даламбера для системы можноИпредставить в другой |
||||||
форме: |
|
|
|
|
|
|
|
F e |
F i |
Ф |
0 . |
(9.7) |
|
|
k |
|
k |
k |
|
|
Из принципа Даламбера для системы в формах (9.6) и (9.7) можно получить следствия в виде уравнений действующих сил и сил инерции. Если просуммировать уравнения (9.6) по всем точкам системы, то
225
|
|
|
n |
|
n |
|
|
n |
|
|
|
|
(9.8) |
|
|
|
F |
R |
Ф 0 . |
|
|
||||||
|
|
|
k 1 |
k |
k 1 |
|
k |
k 1 |
k |
|
|
|
|
Умножая векторно каждое из соотношений (9.6) слева на радиус- |
|||||||||||||
вектор точки rk |
и опять суммируя по точкам системы, получаем |
||||||||||||
|
n |
|
|
|
n |
|
|
|
n |
|
|
|
|
|
rk |
Fk |
rk |
Rk |
rk |
|
Фk 0 |
или |
|
||||
С |
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
n |
n |
|
|
|||||||
|
M 0 |
Fk |
M |
0 Rk |
M |
0 Фk 0 . |
(9.9) |
||||||
|
k 1 |
|
k 1 |
|
k 1 |
|
|
|
|
||||
Векторные уравнения (9.8), (9.9) позволяют получить путем |
|||||||||||||
статике |
|
|
шесть уравнений |
равновесия, |
|||||||||
проецирован я |
на |
оси |
координат |
||||||||||
аналог чных уравнен ям равновесия сил, приложенных к твёрдому телу в , поэтому данный метод решения задач динамики называют также методом к нетостат ки. Если использовать принцип Даламбера в форме
(9.7), то |
бi i |
|
|||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
0; |
(9.10) |
|
|
|
|
|
|
|
F e |
|
|
Ф |
|||||
|
|
|
|
|
|
|
k 1 |
k |
|
k 1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
M 0 |
Fke |
|
|
M |
0 Фk 0 , |
(9.11) |
|||
|
|
|
|
А |
|
||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
т.к. внутренние |
силы |
системы |
|
по |
|
свойству этих сил |
удовлетворяют |
||||||||
условиям |
n |
|
0; |
|
n |
|
|
|
|
0 . |
|
|
|||
|
F |
|
|
M |
0 |
F |
|
|
|
||||||
|
k 1 |
k |
|
|
k 1 |
|
k |
|
|
|
|
|
|||
Если спроецировать уравнения (9.10) и (9.11) на координатные оси, то |
|||||||||||||||
опять получим |
шесть |
уравнений равновесия для сил. |
Особенностью |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Д |
||||
уравнений равновесия сил в форме (9.10), (9.11) является отсутствие в них |
|||||||||||||||
внутренних сил, что делает их особенно удобными при решении многих |
|||||||||||||||
задач динамики системы. Векторное уравнение (9.10) можно получить также, используя теорему о движении центра масс системы, а уравнение (9.11) – из теоремы об изменении кинетического момента механической
системы. Первое слагаемое в уравнении (9.10) есть главный вектор F e внешних сил, действующих на систему, второе слагаемое – главный вектор
Ф сил инерции. В уравнении (9.11) первое слагаемое – главный момент |
||
M 0e внешних сил относительно центра О, второе слагаемое – главный |
||
момент |
|
|
M 0Ф сил инерции. Уравнения (9.10) и (9.11) можно привести к |
||
виду |
F e Ф 0; |
И |
|
M 0e M 0Ф 0. |
|
Решение полученных векторных уравнений осуществляют путём проецирования их на оси координат Oxyz:
226
Fxe Фx 0; Fye Фy 0;
F e Ф 0.
z z
M xe M xФ 0; |
|
|
Мye МФу |
|
(9.12) |
0; |
||
Мe МФ |
|
|
0, |
|
|
z z |
|
|
откуда следует: |
в любой момент времени для движущейся механической |
||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|||
системы суммы главных векторов внешних сил и сил инерции или их проекции |
|||||||||||||||
на оси, а также сумма главных моментов внешних сил и моментов сил инерции |
|||||||||||||||
относительно любого центра (осей координат) равны нулю. |
|
||||||||||||||
Так м образом, все инерционные воздействия на механическую |
|||||||||||||||
систему |
ли твёрдое тело |
можно |
заменить |
одной |
силой, равной Ф и |
||||||||||
инерции |
|
О, и парой сил с моментом, равным |
|||||||||||||
приложенной в центре приведения |
|||||||||||||||
Ф |
|
|
|
|
|
системы |
|
|
|
|
|
||||
M 0 . Главный вектор с л |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
d |
2 |
|
d |
2 |
|
|
|
|
Ф Ф m a |
m |
|
rk |
|
|
m r , |
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
б |
|
|
dt 2 |
k k |
|
||||||||
|
r |
|
k |
k k |
|
|
|
k |
dt 2 |
|
|
||||
но m |
mr , где m – масса системы; r |
– радиус-вектор центра масс. |
|||||||||||||
|
k k |
c |
|
|
|
|
|
c |
|
|
|
|
|
|
|
Следовательно, |
|
|
|
Ф mac . |
|
|
|
||||||||
|
|
|
А |
(9.13) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Главный вектор сил инерции системы равен произведению массы системы |
|||||||||||||||
на ускорение центра масс и направлен в сторону, противоположную ускорению. |
|||||||||||||||
|
|
9.4. Сила инерции тела в частных случаях его движения |
|||||||||||||
|
|
|
|
|
|
Д |
|
||||||||
Главный вектор сил инерции точек твёрдого тела при любом его |
|||||||||||||||
движении определяется уравнением (9.13). |
ля |
определения главного |
|||||||||||||
момента сил инерции относительно центра необходимо выбрать некоторую геометрическую точку в качестве этого центра, называемую центром приведения. Обычно за такую точку принимают центр масс тела С. Рассмотрим некоторые частные случаи движения тела.
9.4.1. Поступательное движение
В этом случае тело не вращается, следовательно,
M |
Ф |
|
|
|
|
|
m |
|
|
|
m |
|
|
|
|
0 , |
C |
r |
Ф |
r |
k |
a |
k |
r |
a |
mr a |
|||||||
поскольку |
|
k |
|
k |
k |
|
|
|
k k |
Иk C C |
||||||
|
r |
0 . |
Инерционные |
|
|
воздействия |
на тело |
приводятся к |
||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равнодействующей, равной главному вектору сил инерции Ф и |
||||||||||||||||
приложенной |
в |
|
центре |
масс |
|
тела |
|
|
Ф maС . |
Направлена |
||||||
равнодействующая в сторону, противоположную ускорению центра масс.
227
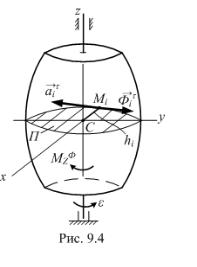
9.4.2. Вращение симметричного тела вокруг главной центральной оси
|
Пусть тело имеет плоскость симметрии П, а ось вращения z |
||||||||||||
перпендикулярна этой плоскости и проходит через центр масс тела С (рис. |
|||||||||||||
9.4). Поместим центр приведения сил инерции в точку С на оси вращения. |
|||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|||
Тогда главный вектор сил инерции тела равен нулю: Ф 0 , т.к. aС 0 . |
|||||||||||||
|
Представим |
тело |
|
как |
совокупность |
|
|
||||||
материальных точек Mi . |
У всех |
точек |
тела |
|
|
||||||||
возникают нормальные |
касательные ускорения |
|
|
||||||||||
вращения |
|
|
|
|
|
|
|
||||||
n |
и |
|
|
|
|
|
|
|
|
|
n |
|
|
ai |
ai |
соответствующие силы инерции Фi , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фi |
. Нормальные с лы |
нерции всех точек тела |
|
|
|||||||||
пересекают |
ось |
|
|
и |
моменты |
|
не |
|
|
||||
создают. |
б |
|
|
|
|
||||||||
|
Главный момент с л инерции формируют |
|
|
||||||||||
только касательные с лы инерции всех точек |
|
|
|||||||||||
тела. Поэтому главный момент сил инерции |
|
|
|||||||||||
равен |
M Ф Ф h |
m h2 . Учитывая, что |
|
|
|||||||||
|
|
z |
i i |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
z |
m h2 , |
|
(9.14) |
|||
используя (9.14), получим |
|
i i |
|
|
|
|
|||||||
M zФ J z . |
|
|
|||||||||||
|
|
|
|
|
|
|
(9.15) |
||||||
|
|
Инерционные воздействия на тело приводятся к паре сил, |
лежащей в |
||||||||||
|
|
|
|
|
|
|
Д |
|
|||||
плоскости, перпендикулярной оси вращения тела. Момент пары сил равен |
|||||||||||||
произведению моментаАинерции тела относительно оси вращения на угловое |
|||||||||||||
ускорение и направлен в сторону, противоположную угловому ускорению. При |
|||||||||||||
решении задач находят модуль момента |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
M zФ J z |
|
, |
|
(9.16) |
||
а его направление показывают на рисунке дуговой стрелкой (см. рис. 9.5). |
|||||||||||||
|
|
|
|
9.4.3. Вращение тела вокруг оси, |
|
|
|||||||
|
|
|
перпендикулярной плоскости симметрии |
|
|
||||||||
|
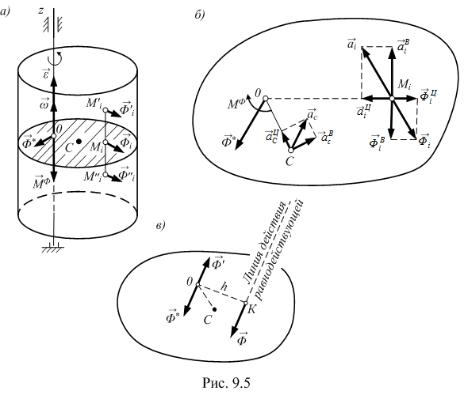
Рассмотрим тело, имеющее плоскость симметрии и вращающееся |
||||||||||||
вокруг неподвижной оси, перпендикулярнойИэтой плоскости и не |
|||||||||||||
проходящей через центр масс тела (рис. 9.5,а). В этом случае неподвижная |
|||||||||||||
ось вращения тела является главной осью инерции тела в точке О. Каждой |
|||||||||||||
точке |
M i' |
(см. рис. 9.5,а) |
соответствует |
точка Mi'' такой |
же массы, |
||||||||
симметричная относительно заданной плоскости (на рис. 9.5,а эта плоскость заштрихована). Из кинематики известно, что ускорения всех точек, лежащих на одной прямой, параллельной оси вращения,
228
|
|
|
|
|
|
|
|
||||
геометрически равны. Поэтому силы инерции Фi |
mi ai |
и Фi |
mi ai |
||
точек M i' и Mi'' геометрически равны и их равнодействующая приложена к |
|||||
точке M i , лежащей в плоскости симметрии. Отсюда следует, что в точке |
|||||
M i приложена равнодействующая сил инерции всех точек тела, |
лежащих |
||||
С |
|
|
|
|
|
на перпендикуляре к плоскости симметрии, восстановленном в этой точке. |
|||||
Таким образом, сложение сил инерции точек тела в этом случае движения сводится к сложению сил инерции точек плоской материальной фигуры, имеющей массу данного тела и тот же момент инерции относительно оси вращен я (р с. 9.5,б).
и |
|
||
|
|
б |
|
|
|
А |
|
|
Приведём силы инерции точек фигуры к центру её вращения О. При |
||
|
|
Д |
|
приведении получим силу, приложенную в этом центре, и пару сил, |
|||
лежащую в плоскости фигуры. |
|
||
|
Сила инерции равна главному вектору, определяемому формулой |
||
Ф maС . |
|
|
|
|
Для определения момента пары M Ф разложим силу инерции каждой |
||
|
|
|
И |
точки на вращательную и центробежную силы инерции, направленные противоположно вращательному и центростремительному ускорениям этой точки.
Их модули определим по формулам |
|
|
||
ФВ m aВ m r ; |
ФЦ m aЦ m r 2 . |
|||
i |
i i i i |
i |
i i |
i i |
229
Так как линии действия центробежных сил инерции проходят через центр вращения О, то искомый момент пары равен сумме моментов
вращательных сил инерции относительно точки О: M Ф M0Ф mi ri2 . Таким образом, алгебраическая величина момента пары, составленной
силами инерции, |
M Ф – J z , где Jz – момент инерции тела относительно |
|||||
С |
|
|
|
|
||
оси вращения; – алгебраическая величина углового ускорения тела. |
||||||
Вектор M Ф |
направлен перпендикулярно плоскости фигуры, т. е. |
|||||
совпадает с осью вращения тела и направлен противоположно вектору |
||||||
углового ускорен |
я: |
|
|
|
||
плоскости |
|
|
||||
|
|
|
M Ф J z . |
|
||
Как звестно |
|
з стат ки, силу Ф* и пару с моментом M Ф, |
лежащие в |
|||
одной |
|
, можно заменить одной действующей силой Ф, |
||||
|
образом |
|
||||
геометр чески равной главному вектору (рис. 9.5,в). |
|
|||||
Л н я действ я этой силы отстоит от центра приведения О на |
||||||
расстоян |
|
|
|
M Ф |
|
|
|
|
|
А |
|
||
|
|
|
h = |
Ф |
. |
(9.17) |
Таким |
|
|
, при вращении твёрдого тела, имеющего плоскость |
|||
материальной симметрии, вокруг оси, перпендикулярной этой плоскости, силы инерции точек тела приводятся к равнодействующей силе, лежащей в плоскости симметрии.
|
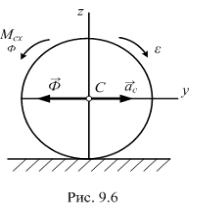
9.4.4. Плоское движение симметричного тела |
|||
Пусть твёрдое тело имеет плоскость |
|
|||
материальной |
симметрии |
и |
совершает |
|
движение, при котором |
все |
точки тела |
|
|
перемещаются |
параллельно |
|
Д |
|
этой плоскости |
И |
|||
(рис. 9.6). Плоское движение тела слагается из |
||||
поступательного движения вместе с центром |
||||
масс и вращательного вокруг оси, проходящей |
||||
через центр масс перпендикулярно плоскости |
||||
материальной симметрии.
|
|
Силы инерции приводятся к главному вектору |
Ф mac , |
приложенному к центру масс и к паре сил с моментом |
M cxФ – Jcx . |
Главный вектор сил инерции и результирующая пара сил инерции так же, как и центр масс тела, лежат в плоскости материальной симметрии.
230
