5. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА
Простейшими движениями твёрдого тела являются поступательное движение и вращение вокруг неподвижной оси.
5.1. Поступательное движение твёрдого тела |
С |
Поступательным движением твёрдого тела называют такое его движение, |
при котором |
любая прямая, жёстко соединённая с телом, остаётся |
параллельной |
своему первоначальному положению в каждый момент |
времени. |
|
|
|
|
|
|
|
|
|
траекторскорости, ускорения всех точек |
|
|
|
Траектор |
точек |
поступательно |
|
|
|
движущегося твёрдого тела могут быть |
|
|
|
прямыми |
любыми кр выми. |
|
|
|
|
|
войства |
поступательного |
движения |
|
|
|
тела |
|
б |
|
|
|
характер зует |
теорема: |
при |
|
|
|
поступательном |
дв жен |
твёрдого |
тела |
|
|
|
тела од наковы. Рассмотр м две точки |
и В |
|
|
|
твёрдого тела. |
А |
|
Радиусы-векторы этих точек удовлетворяют условию (рис. 5.1) |
|
|
|
|
|
|
|
|
В. |
|
|
|
|
|
|
rB |
rA |
|
(5.1) |
Для любого твёрдого тела вектор |
В |
является |
постоянным по |
модулю, |
а |
при поступательном |
движении он не изменяется и по |
направлению. |
|
|
Д |
|
|
|
|
|
|
|
Уравнение (5.1) показывает, что годограф радиуса-вектора точки В, являющийся траекторией этой точки, сдвинут по сравнению с годографом
радиуса-вектора точки А на постоянный вектор АВ. Если этот сдвиг осуществить, то обе траектории совпадут всеми своими точками. Такие траектории являются одинаковыми.
Если продифференцировать по времени уравнение (5.1), то получим
|
|
drB |
|
drA |
|
d |
AB . |
|
|
|
|
|
|
dt |
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
В этом соотношении |
drB |
V |
; |
|
drA |
V |
A |
. |
Кроме того, для AB – |
|
dt |
|
B |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
И |
постоянного по модулю и направления вектора |
|
d |
AB 0. |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, для любого момента времени имеем |
|
|
|
|
|
VB VA . |
|
|
|
(5.2) |
Дифференцируя по времени (5.2) и учитывая, что
|
dVB |
a |
|
; |
|
dV A |
a |
|
, |
|
|
|
|
|
|
|
|
dt |
B |
|
|
dt |
A |
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
|
|
|
|
|
|
|
|
a B |
|
aA . |
|
|
(5.3) |
Теорема о поступательном движении твёрдого тела доказана. |
С |
|
|
|
|
|
|
|
|
Движение твёрдого тела, для которого векторы скоростей точек равны |
только в один момент времени, |
а не всё время, |
называется мгновенным |
поступательным дв жен ем. Для мгновенного поступательного движения ускорен я точек в общем случае не являются одинаковыми.
Поступательное дв жение твёрдого тела полностью определяется
движен |
ем одной его точки уравнениями |
|
|
|
x f1 t ; |
y f 2 t ; |
z f3 t . |
(5.4) |
ледовательно, сво одное твёрдое тело, совершающее поступательное |
движен |
, меет три степени |
|
и уравнения |
(5.4) являются |
кинемат
уравнен ямисвободыпоступательного движения твёрдого тела. Для описания поступательного движения твёрдого тела используют
кинемат ку точки.
движение, при которомАимеется геометрическое место неподвижных точек тела (ось вращения) в течение всего времени движения. При этом остаются неподвижными все точки тела, расположенные на прямой, проходящей
5.2. Вращательное движение твёрдого тела
5.2.1. Угол поворота, угловая скорость и угловое ускорение
Вращением твёрдого тела вокруг неподвижной оси называют такое его
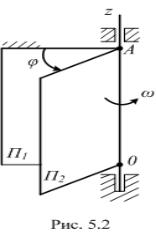
Если А и О – неподвижные точкиДтела (рис. 5.2), то осью вращения является ось Oz. Одно направление оси Oz принимается за положительное.
через его неподвижные точки.
плоскость П1 и подвижную плоскость П2 , котораяИ может быть совмещена с вращающимся телом. Пусть в начальный момент времени обе плоскости
Через ось вращения проведём неподвижную
совпадают. Тогда в момент времени t положение вращающегося тела можно определить двугранным углом φ между плоскостями (рис. 5.2).
Угол φ называют углом поворота тела (угловой координатой).
Положение вращающегося тела в момент времени t задают уравнением
где f t – любая дважды дифференцируемая функция времени.
Это уравнение называют уравнением вращения твёрдого тела вокруг
неподвижной оси.
Тело, совершающее вращение вокруг неподвижной оси, имеет одну степень свободы, так как его положение определяется заданием только одного параметра – угла φ. Угол φ в уравнении (5.5) задают в радианах. Угол φ считают положительным, если, смотря навстречу принятому
направлен ю оси Oz, мы видим вращение тела, происходящее против часовой стрелки. Пр знаком вращательного движения тела является то,
что траектор |
точек тела при его вращении вокруг неподвижной оси |
Сявляются |
, |
расположенными |
в |
плоскостях, |
перпенд кулярных оси вращения. |
|
|
Для характер ст ки вращательного движения твёрдого тела вокруг |
неподв жной |
оси |
спользуют |
понятия угловой |
скорости |
и углового |
ускорен я. |
|
|
|
|
|
окружностямиАлгебра ческой угловой скоростью тела в какой-либо момент времени
называют первую про зводную по времени от угла поворота. Она является
величиной полож тельной при вращении тела против часовой стрелки, так |
как угол поворота возрастает с течением времени. |
|
Угловуюбскорость о означают . |
|
Тогда |
d |
|
|
(5.6) |
|
А. |
Драд/с.
Втехнике частоту вращения n тела выражают в оборотах в минуту. Связь частоты вращения n с угловой скоростьюИимеет вид. (5.8)
|
|
|
|
dt |
dt2 |
|
Размерность углового ускорения получают из формулы (5.8): |
Если |
0 |
при |
0 |
рад/с2 . |
, алгебраическая угловая скорость возрастает с |
|
|
|
|
|
|
|
течением |
времени |
и, следовательно, |
тело вращается ускоренно в |
рассматриваемый момент времени в положительную сторону (против часовой стрелки). При 0 0, т. е. ускоренное вращение совершается
в отрицательную сторону.
Угловую скорость и угловое ускорение на рисунках изображают дуговыми стрелками вокруг оси вращения. Дуговая стрелка для угловой скорости указывает направление вращения тела (см. рис. 5.2).
Для ускоренного вращения дуговые стрелки для угловой скорости и углового ускорения имеют одинаковые направления, для замедленного – их направлен я прот воположны.
численная |
|
|
|
5.2.2. Уравнен я параметры при равномерном и равнопеременном |
С |
|
вращениях тела |
|
Равномерным называется такое вращение твёрдого тела, при котором |
вел ч на угловой скорости |
всё время остаётся постоянной: |
const . Тогда |
d |
0 . Найдём уравнение равномерного вращения. |
|
|
dt |
|
|
|
|
Из формулы |
d |
получим |
t |
t . |
d dt или 0 |
|
|
А |
|
|
|
dt |
|
0 |
0 |
|
Так какбconst , окончательно находим уравнение равномерного |
вращения тела в виде |
|
|
|
|
|
|
|
|
0 t , |
(5.9) |
|
|
|
|
Д |
где 0 – начальный угол поворота тела. |
|
|
Следует отметить совпадение структур формулы (11.29) равномерного движения точки и равномерного вращения тела (5.9).
Равнопеременным называют такое вращение твёрдого тела, при
котором угловое ускорение всё время остаётся постоянным: const . |
|
|
|
|
|
И |
Найдём уравнение равнопеременного вращения, считая, что при t0 0 |
начальный угол 0, начальная угловая скорость |
0 . Согласно формуле |
(5.8), d |
|
или d dt . |
|
|
|
|
dt |
|
const , то, взяв от обеих |
частей |
последнего |
равенства |
Так |
как |
интегралы в соответствующих пределах, получим |
|
|
|
|
|
0 |
t . |
|
|
(5.10) |
Представим эту |
формулу в |
виде |
d |
0 t или, |
разделяя |
|
|
|
|
|
dt |
|
|
переменные, |
найдем |
d 0 dt tdt . |
Вторично интегрируя, найдём |
уравнение равнопеременного вращения тела: |
|
|
|
0 |
0t |
t 2 |
. |
(5.11) |
|
2 |
|
|
|
|
|
|
Если при вращении тела модуль угловой скорости возрастает, то |
|
вращение равноускоренное ( 0 ), |
а если убывает – |
равнозамедленное |
|
( 0 ). Утверждение справедливо при вращении тела в положительном |
|
С |
|
|
|
|
|
направлении угла поворота . |
|
|
|
|
Отметим совпадение структур формул (4.30), (4.31) равнопеременного движен я точки (5.10), (5.11) равнопеременного вращения тела.
Пр мер. Угловая скорость |
вала |
двигателя 0 120 рад/c |
число |
t |
4 |
вследств е увел чен я нагрузки упала в течение 4 с до 80 рад/c.
Выч сл ть угловое ускорение , считая его постоянным, а также оборотов N, совершённых двигателем за это время.
|
Решен е. Зап шем уравнение (5.10) равнопеременного вращения |
|
обороте |
|
|
|
|
|
|
|
0 |
t , |
откуда |
|
|
0 |
|
80 120 |
10 рад/c 2 . |
|
Угловое |
ускорен е |
|
отрицательно, |
поскольку |
движение |
|
равнозамедленное. |
В |
одном |
|
|
содержится 2 радиан, |
|
|
|
А |
|
|
|
|
следовательно, угол поворота , соответствующий N оборотам двигателя, |
|
равен 2 N . Отсюда |
|
N |
|
|
|
|
|
|
|
|
|
|
0 0 , найдем 0t |
t 2 |
120 4 |
10 16 |
400 рад; |
N |
400 |
63,7 об. |
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5.3. Скорости и ускорения точек вращающегося тела |
|
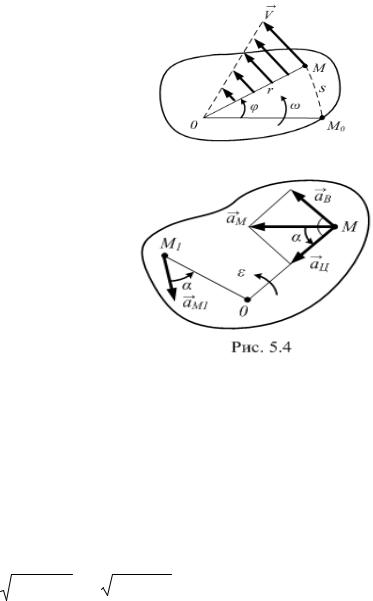
Пусть задано уравнение вращения твёрдого тела вокруг неподвижной |
|
оси f t |
(рис. 5.3). Расстояние s точки М по |
дуге окружности, |
|
отсчитываемое от неподвижной точкиДМ0 , выражается зависимостью |
|
s r , где r |
– радиус вращения точки тела; |
φ – угол поворота тела. У |
каждой точки тела радиус вращения остаётся неизменным при вращении
тела вокруг неподвижной оси, перпендикулярной чертежу в точке О. |
|
Алгебраическую скорость точки М определяют по формуле |
|
ds |
|
d |
И |
V dt |
r |
dt |
r . |
(5.12) |
|
Скорости точек тела при вращении |
|
|
|
пропорциональны расстояниям от точек тела |
|
|
|
до |
оси |
|
вращения. |
|
Коэффициентом |
|
|
|
пропорциональности |
|
является |
|
|
угловая |
|
|
|
скорость. Скорости точек направлены по |
|
|
|
касательным к траекториям и, следовательно, |
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярны радиусам вращения. |
|
|
Рис. 5.3 |
|
|
|
корости точек тела, расположенных |
|
|
|
на отрезке прямой ОМ, в соответствии с |
|
|
|
линейному |
|
|
|
|
|
по |
|
|
|
выражен ем |
(5.12) |
распределены |
|
|
|
|
|
|
закону. |
Векторы |
|
скоростей |
|
|
|
точек отрезка вза мно параллельны и их |
|
|
|
концы располагаются на одной прямой, |
|
|
|
|
|
|
б |
|
|
|
|
проходящей через ось вращения. |
|
|
|
|
|
|
|
|
|
Ускорен е точки М разлагаем на |
|
|
|
вращательную |
|
центростремительную |
|
|
|
составляющ е (р с. 5.4): |
aM aВ aЦ . |
|
|
|
|
|
|
При |
|
|
|
А |
и нормальное |
|
вращательном |
движении |
тела |
касательное |
ускорения точки тела называют вращательным и центростремительным и |
соответственно о означают |
a , |
|
a или aВ, aЦ . Вращательное и |
центростремительное |
ускорения |
|
вычисляют по формулам |
aB r ; |
|
r 2 |
|
V 2 |
|
|
|
|
|
|
Д |
|
aЦ |
|
r |
. Из рис. 5.4 полное ускорение точки М при вращении тела |
равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aM |
aВ2 |
|
aЦ2 |
r |
2 4 . |
|
|
(5.13) |
|
Касательные, нормальные |
и |
полные |
ускорения точек тела, как и |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
скорости, распределены по линейному закону. Они линейно зависят от |
расстояний точек до оси вращения. Нормальное ускорение направлено по |
радиусу r к оси вращения. Направление вращательного ускорения зависит |
от знака алгебраического углового ускорения. При 0 |
и 0 или 0 |
и 0 имеем ускоренное вращение тела, |
направления векторов |
a и V |
совпадают. Если и имеют разные знаки (замедленное вращение), то |
a |
и V направлены противоположно друг другу. Обозначив через угол |
между полным ускорением точки и радиусом вращения, получим |
|
|
|
|
|
|
|
|
tg |
aВ |
|
|
|
. |
|
|
|
(5.14) |
|
|
|
|
|
|
aЦ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Угол для всех точек тела является постоянным, т. к. не зависит от радиуса вращения.
6.ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
6.1.Уравнения плоского движения твёрдого тела
Плоским движением твёрдого тела называют |
|
|
С |
|
|
|
|
|
|
такое движение, при котором все точки |
|
|
сечения тела движутся в своей плоскости. |
|
|
|
Пусть твёрдое тело 1 совершает плоское |
|
|
движен е |
(р с. |
6.1). Секущая плоскость П1 |
в |
|
|
жение |
П, |
которое |
|
|
теле 1 |
образует |
сечение |
Рис. 6.1 |
перемещается в секущей плоскости П1. |
|
|
|
Если параллельно плоскости П1 выполнить другие сечения тела, |
например через точки А2, А3 |
т.д., лежащие на одном перпендикуляре к |
сечениям, то все эти точки и все сечения тела будут перемещаться |
одинаково. |
б |
|
|
|
|
|
|
|
|
|
|
|
Следовательно, дв |
тела в этом случае |
|
|
полностью определяется движением одного из |
|
|
его сечен й в какой-ли о из параллельных |
|
|
|
|
А |
|
плоскостей, а положение сечения – положением |
|
|
двух точек этого сечения, например |
и В (рис. |
|
|
6.2). Положение сечения П в плоскости Оxy |
|
|
определяют |
положением |
отрезка |
В, |
|
|
проведённого в этом сечении. |
|
|
|
(хА, уА) и |
В(хВ, уВ) |
Положение |
двух |
точек |
на |
плоскости |
характеризуется четырьмя параметрами (координатами), на которые |
накладывают одно ограничение – уравнение связи в виде длины отрезка |
АВ: |
|
|
(хА – хВ)2 + (уА – уВ )2 = В2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
Поэтому положение сечения П в плоскости можно задать тремя |
независимыми параметрами – координатамиДхА, уА точки А и углом φ, |
который образует отрезок АВ с осью Оx. Точку А, выбранную для |
определения положения сечения П, называют полюсом. |
|
При движении сечения тела его кинематические параметры являются |
функциями времени |
хА=х(t); |
уА=у(t); φ=φ(t) . |
(6.1) |
Уравнения |
|
(6.1) являются |
кинематическими |
уравнениями |
плоского |
(плоскопараллельного) движения твёрдого тела. Теперь покажем, что в соответствии с полученными уравнениями (6.1) тело при плоском движении совершает поступательное и вращательное движения. Пусть на рис. 6.3 сечение тела, заданное отрезком А1В1 в системе координат Oxy, переместилось из начального положения 1 в конечное положение 2.
187

Покажем |
два способа |
возможного |
|
перемещения тела из положения 1 в |
|
положение 2. |
|
|
|
|
Первый способ. За полюс примем |
|
точку А1. Перемещаем отрезок А1В1 |
|
параллельно |
самому |
себе, |
т.е. |
|
поступательно, по траектории А1, А2 до |
|
совмещения точек А1 и А2. |
|
' . Далее поворачиваем этот отрезок |
Получаем положен е отрезка А В |
|
|
2 |
1 |
|
вокруг полюса А2 на угол φ и получаем конечное положение плоской |
фигуры |
|
' |
, заданное отрезком А2В2. |
|
|
Второй способ. За полюс примем точку В . Перемещаем отрезок А В |
С |
|
1 |
1 1 |
параллельно |
самому се е, |
т.е. поступательно |
по траектории В1В2 до |
1.Плоскоебдв жен е в полном соответствии с уравнениями (6.1) представляет со ой Асовокупность поступательного и вращательного движений, причём модель плоского движения тела можно рассматривать как поступательное движение всех точек тела вместе с полюсом и вращение тела относительно полюса.
2.Траектории поступательного движения тела зависят от выбора полюса. На рис. 6.3 в рассмотренномДслучае видим, что в первом способе движения, когда за полюс принимали точку А1, траектория поступательного движения 1 2 значительно отличается от траектории В1В2 для другого полюса В.
3.Вращение тела от выбора полюса не зависит. Угол φ вращения тела остаётся постоянным по модулю и направлениюИвращения. В обоих случаях, рассмотренных на рис. 6.3, вращение произошло против вращения часовой стрелки.
6.2.Основные кинематические характеристики плоского движениясовмещен я точек В В . Получаем положение отрезка В А . Далее
плоском движении являются: траектория движения полюса, угол вращения тела вокруг полюса, скорость и ускорения полюса, угловая скорость и угловое ускорение тела (рис. 6.4).
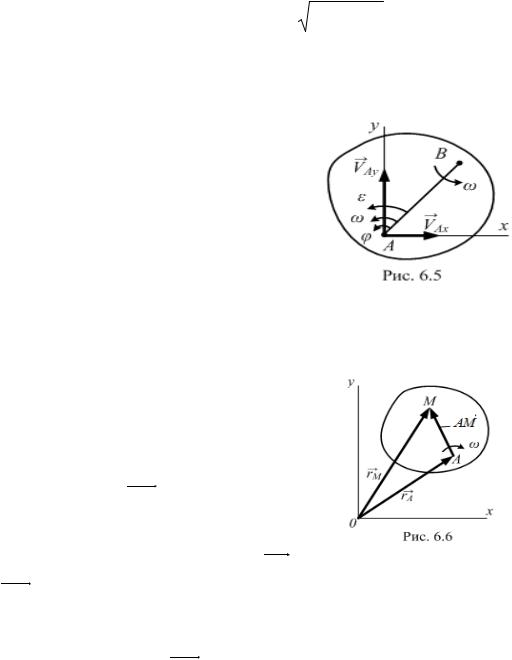
Дополнительные оси О1x1y1 при поступательном движении перемещаютcя вместе с полюсом А параллельно основным осям Оxy по траектории движения полюса. Таким образом, плоскопараллельное движение является простейшим сложным движением тела, которое выделено в самостоятельную категорию в связи с тем, что на теории плоского движения в теоретической механике строятся теории сложных движений тел и механических систем.
корость полюса плоской фигуры можно определить с помощью производных по времени от уравнений (6.1):
|
|
|
VAx |
dхA |
; |
VAy |
dyA ; |
|
|
VA VAx2 VAy2 . |
|
|
|
|
|
|
скорости |
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
САналог чно определяют |
угловые характеристики тела: угловую |
скорость |
|
d |
; угловое ускорение |
d |
|
d 2 |
. |
dt |
dt |
dt2 |
На |
|
выбора |
|
|
|
с. 6.5 в полюсе А показаны проекции |
вектора |
|
|
|
VA на оси Ox, Oy. Угол вращения |
тела φ, угловая скорость ω и угловое ускорение |
показаны дуговыми стрелками вокруг точки |
. В |
связи |
с |
|
независимостью |
вращательных |
характеристик |
движения |
от |
|
|
|
|
полюса |
угловые характеристики φ, ω, ε можно показывать |
в любой точке плоской фигуры дуговыми |
стрелками, например в точке В. |
|
Д |
|
|
|
|
|
|
|
|
|
|
|
6.3. ТеоремаАо сложении скоростей точек тела |
Для сечения плоской фигуры на рис. 6.6 точка А |
принята |
за |
полюс. Положение |
полюса |
определено |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
радиусом-вектором rA , проведённым из начала |
координат в точку А. Требуется установить связь |
скорости точки М тела с характеристиками плоского |
движения |
тела. |
Отрезок |
AМ |
|
постоянной |
длины |
рассматривается как вектор, определяющий положение точки М относительно полюса А.
Запишем векторное равенство rM rA AМ , где rA – радиус-вектор
полюса А; AM – радиус-вектор, определяющий положение точки М относительно полюса А. Вектор скорости точки М есть производная от радиуса-вектора rM по времени
VM drA d AM |
или |
VM VA VMA . |
(6.2) |
dt |
dt |
|
|
|
В полученном уравнении VA – скорость полюса; VMA – скорость точки М, которую она получает при вращении тела вокруг полюса А:
VMA AM |
|
или VMA AM , |
где ω – угловая скорость вращения тела; – вектор угловой скорости |
тела. |
|
На рис. 6.6 угловая скорость ω показана дуговой стрелкой, при этом |
|
|
|
|
|
|
|
|
|
|
|
вектор угловой скорости перпендикулярен чертежу в точке А и |
направлен от нас. Так м образом, |
доказана теорема о сложении скоростей |
точки плоской ф гуры. |
|
|
|
|
|
|
|
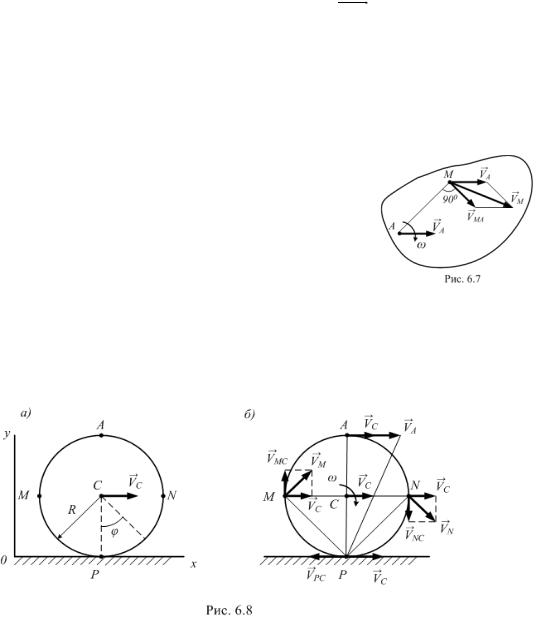
Теорема. Скорость любой точки М тела при |
скорости |
|
|
|
|
|
|
|
плоском дв жен |
геометрически |
|
складывается |
из |
Сполюса скорости вращения точки М вокруг |
полюса (р с. 6.7). Направление скорости VM |
можно |
найти |
|
геометр ческим |
|
построением |
|
б |
|
|
|
|
|
параллелограмма векторов скоростей по уравнению |
(6.2). |
|
|
|
|
|
|
|
|
|
|
|
Пр мер 1. |
|
|
|
|
|
|
|
|
|
|
Колесо рад усом R катится |
|
ез скольжения по рельсу. Скорость |
|
|
|
А |
центра колеса |
VC . Определить скорости точек обода колеса Р, М, А, N |
(рис. 6.8, а). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
Решение. Запишем уравнения движения колеса для рис. 6.8: |
|
|
|
хC VC t ; |
yC R ; |
|
xC |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
За полюс принимаем точку Р. Определим угловуюИскорость вращения |
точки С вокруг полюса Р: |
VC |
. Теперь за полюс примем точку С и |
|
|
|
|
|
R |
|
|
|
|
|
применим к точке Р колеса (рис. 6.8,б) теорему о |
скоростях при плоском |
движении: VP VC VPC . Отметим, что VPC |
CP ; |
VPC R |
VC |
R VC . |
|
|
|
|
|
|
|
|
|
|
|
R |