Файловый архив студентов. Файловый архив студентов.
1262 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Сибирская государственная автомобильно-дорожная академия
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

2192

.pdf
Скачиваний:
7
Добавлен:
07.01.2021
Размер:
3.87 Mб
Скачать
☆

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

ТЕОРИЯ

 

ВЕКТОРНЫХ МОМЕНТОВ СИЛЫ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.1. Алгебраический момент силы относительно точки

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для

плоской

 

 

 

 

 

системы

сил,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

приложенных к твердому телу, используют

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

понятие алгебраического

 

 

 

момента

силы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

относительно точки.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алгебра

ческ

м

 

 

 

моментом

силы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

относительно

 

 

 

 

 

 

 

 

точки

 

 

 

 

 

 

 

 

называют

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

произведен е модуля силы на плечо

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ли

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

силы относ

тельно этой точки, взятое со

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Сзнаком плюс ли м нус (рис. 2.1).

 

 

 

 

 

точки

называют кратчайшее

 

 

 

 

 

 

 

Плечом

h с лы

 

 

F

 

 

 

относительно

 

расстоян е между этой точкой и линией действия силы, т.е.

длину

 

перпенд куляра, опущенного из точки О на линию действия силы F .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Обознач м М

О

( F )

 

 

 

 

М

О

алгебраический момент силы F

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

относительно точки О.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

( F ) = Fh .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

М

О

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(2.1)

 

 

 

 

 

 

 

Если силабстремится вращать тело

вокруг

 

 

данной точки

против

 

часовой стрелки, то

 

ерем знак плюс, если по часовой стрелке знак

 

минус.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Д

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из определения алгебраического момента силы относительно точки

 

 

следует, что он не зависитАот переноса силы вдоль линии ее действия.

 

 

Численно алгебраический момент относительно точки равен удвоенной

 

 

площади треугольника, построенного на силе В и моментной точке:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МО ( F ) =

 

 

 

 

 

 

 

 

 

 

 

 

 

И

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 пл.

ОАВ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(2.2)

151

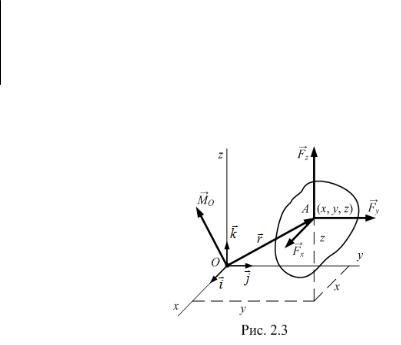
2.2. Векторный момент силы относительно точки

Векторным моментом силы относительно точки называют вектор,

приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки, расположенный перпендикулярно плоскости, в которой лежат сила и моментная точка, и направленный так, чтобы, смотря навстречу вектору, видеть силу, стремящуюся вращать тело против движения часовой стрелки

(рис. 2.2).

 

Векторный

момент

силы

 

F

 

 

 

определению

М

( F ) или

 

 

относительно точки О обозначим

 

 

С

 

 

О

 

 

 

 

 

 

 

 

МО , а его ч словую вел чину

МО (F )

.

 

 

 

 

 

 

Тогда, согласно

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

М

О (F )

 

= Fh .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Как

для

алге раического

момента,

 

 

векторный момент с лы относительно точки

 

 

равен удвоенной площади треугольника,

 

 

построенного на силе и моментной точке:

 

 

 

МО (F )

 

 

= б2 пл. ОАВ.

 

 

 

 

 

 

 

 

 

Справедлива формула

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

r

 

(2.3)

 

 

 

 

 

 

 

 

 

M O (F)

F ,

 

 

 

 

 

 

 

 

 

 

 

 

Д

 

где r радиус-векторА, проведенный из моментной точки О в точку

приложения силы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Покажем

справедливость

векторного

выражения (2.3) следующим

образом.

Угол

 

между векторами

r

и

F

 

равен (r , F) . Тогда из

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

И

прямоугольного треугольника ОАС найдем плечо силы h = r sin

и модуль момента силы

МО = F r sin .

152

Формула модуля векторного выражения (2.3) совпадает с полученной

формулой

 

для

МО .

Значит,

 

действительно формула (2.3) является

векторным моментом силы F относительно точки О.

 

 

Вектор

r F

 

перпендикулярен плоскости, в которой расположены

векторы

 

r

 

 

 

 

F , т.е. плоскости треугольника ОАВ, которой

перпенд кулярен

 

векторный момент МО ( F ).

 

 

 

 

Так м образом, векторный

 

момент МО

является

третьим вектором,

приложенным в центре О, перпендикулярно векторам

r и

F ,

направленным

С

 

 

 

вектору МО видеть

 

F ,

 

так, чтобы смотря навстречу

силу

стремящуюся

вращать тело прот в часовой стрелки.

 

 

 

 

 

Если с ла F дана своими проекциями Fx ,

Fy ,

Fz на оси координат и

даны коорд наты

 

x, y, z

 

 

 

приложения этой силы (рис. 2 3), то

точки

 

 

 

 

 

 

векторный момент с лы относительно начала координат можно записать с

помощью определ теля

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

j

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МО(F )= r

 

 

 

б

xFz ) j (xFy yFx )k , (2.4)

F

 

 

x

 

y

z

( yFz

zFy ) i (zFx

 

 

 

 

 

Fx Fy Fz

 

 

 

 

 

 

 

 

где i , j ,

k

 

А

 

 

 

единичные векторы осей координат.

 

 

Выражения в круглых скобках перед

 

 

 

 

векторами

 

i ,

j ,

k

формулы (2.4)

 

 

 

 

являются проекциями вектора

МО

( F ) на

 

 

 

 

оси координат:

 

 

 

 

 

 

Д

 

 

 

 

 

 

 

 

И

 

 

 

 

 

 

 

 

 

 

 

 

МОx (F) yFz zFy ;

 

 

 

 

 

 

(2.5)

МОy (F) zFx xFz ;

 

 

 

М

Оz

(F) xF

yF .

 

 

 

 

 

 

 

 

 

 

y

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Модуль векторного момента МО ( F ) и косинусы его углов с осями координат определяют по формулам

153

 

 

 

 

(F)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

М

О

 

( yF

zF

y

)2

(zF

xF

)2 (xF

y

 

yF )2 ;

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

x

z

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

М

Оx (F)

 

 

 

 

 

 

МОy

(F)

 

 

 

 

 

cos(М

О ,i )

 

 

 

 

 

 

 

;

 

cos(МО ,

j)

 

 

 

 

 

 

 

 

;

 

(2.6)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

М

О (F)

 

 

 

 

 

 

 

 

 

МО (F)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МОz (F)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos(М

О , k )

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МО (F)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В формулах (2.6) ч словую величину МО(F ) берем со знаком плюс.

относительно

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.3. Момент силы относительно оси

 

 

 

Моментом

лы

 

относительно

оси

Оz

называют алгебраический

момент

 

Мz

 

проекц

 

 

 

этой силы на плоскость, перпендикулярную

 

 

б

 

 

 

 

 

 

 

 

 

 

 

 

оси, относ тельно точки пересечения оси с этой плоскостью (рис. 2.4).

Момент

 

с лы

 

 

 

 

 

 

 

 

 

 

 

 

оси

считают

 

 

положительным,

если,

смотря

 

навстречу

 

оси, видим проекцию силы на

плоскость,

перпенд кулярную оси,

 

стремящуюся вращать

тело

 

против

часовой

 

 

 

 

 

 

 

 

А

 

 

 

 

 

 

стрелки, и отрицательным, если она

 

 

 

 

 

 

 

 

 

 

 

 

 

стремится вращать тело по часовой

 

 

 

 

 

 

 

 

 

 

 

 

 

стрелке.

 

 

 

 

 

F на плоскость

 

 

 

 

 

 

 

 

 

 

 

 

 

Проекция силы

 

 

 

 

 

 

 

 

 

 

 

 

 

рассматривается как вектор FП .

 

 

Д

 

Момент

 

 

силы,

 

 

например,

 

 

 

 

 

 

 

 

 

 

 

 

 

относительно

оси

 

Oz

 

обозначим

 

 

 

 

 

 

 

 

 

 

 

 

 

Мz (F) . По определению,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мz Мz (F)

= МО (FП ) = hF cos h FП ,

 

 

(2.7)

где FП

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

И

вектор проекции силы F на плоскость П, перпендикулярную оси

Оz; О точка пересечения оси Оz с плоскостью П; угол вектора силы

F с плоскостью П.

Из определения момента силы относительно оси следует, что алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь

треугольника, построенного на проекции силы FП и точке пересечения О

оси с плоскостью:

 

 

Мz Мz (F) = h FП

= 2 пл. ОА1В1.

(2.8)

154

2.4. Связь момента силы относительно оси с векторным моментом силы относительно точки на оси

Используя формулу (2.2) и рис. 2.5,

 

запишем момент силы относительно оси:

 

 

Мz = Мz (F) = 2 пл. ОА1В1.

(2.9)

 

С

 

 

относительно

 

Векторный момент силы F

 

точки О, взятой на пересечении оси Оz с

 

перпенд кулярной плоскостью П, равен

 

 

МО =

МО(F )

= 2 пл. ОАВ.

(2.10)

 

фигуры

 

 

1 1

 

Векторный момент МO ( F ) направлен перпендикулярно плоскости

треугольн ка ОАВ. Из геометрии известно, что площадь проекции плоской

равна площади проецируемой фигуры, умноженной на косинус

угла между плоскостями, в которых расположены эти фигуры. Угол между

 

б

перпендикулярами

к этим

плоскостями змеряется

углом

между

плоскостям. Перпенд куляром к плоскости треугольника ОА В

является

ось Oz, а перпенд куляр

к плоскости треугольника ОАВ векторный

момент МО ( F ). Так м о разом, 2 пл. ОА1В1 = 2пл. ОАВcos , где

 

 

А

 

угол между вектором МО ( F ) и осью Оz. Отсюда имеем

 

 

 

 

 

 

 

cos .

 

 

 

Мz (F) =

МО

(F )

(2.11)

 

 

 

Мz = МО cos .

 

(2.12)

 

 

 

 

 

Д

 

2.5.Теорема высот треугольника

 

На рис. 2.6 сила F , совпадающая со стороной АВ треугольника АВС, стремится вращать твердое тело относительно точки С.

Моментом МC (F )

силы

F относительно центра С является

произведение силы

 

И

F на плечо h, которое совпадает с высотой h

треугольника, опущенной из вершины С на основание АВ.

Для определения высоты h треугольника удобно пользоваться теоремой, которую в 2010 г. предложили В.Н. Тарасов и .В. Бояркина:

квадрат высоты вершины треугольника равен разности квадратов гипотенузы и катета: гипотенуза равна произведению двух сторон, образующих вершину, поделенному на основание; катет равен сумме квадратов сторон, образующих

эту вершину минус квадрат основания, поделенные на удвоенное основание.

Для треугольника АВС (см. рис. 2.6) стороны которого известны: ВС=а;

АС=b; АВ=с, имеем

 

 

a b

2

 

2

b

2

c

2

2

 

h

2

 

a

 

 

 

 

(2.13)

 

 

c

 

 

 

 

2c

 

 

.

 

 

 

 

 

 

 

 

 

 

 

155

Теорема высот треугольника сформулирована для произвольного

треугольн ка,

поэтому можно использовать ее для частного случая,

когда

треугольн к

прямоугольный (рис. 2.7),

где сила F, совпадающая с

АВС

 

 

 

 

 

 

относительно вершины С

основан ем АВ=с

 

 

 

вращать

тело

прямого угла. Плечо h силы

F

тоже определяется по теореме высот

треугольн ка

 

h

2

 

a b 2

 

 

(2.14)

 

 

 

.

 

 

стремится

c

 

 

 

 

 

3.

 

 

 

 

ВНОВЕСИЯ СИЛ

 

б

 

 

 

3.1. Условия равновесия пространственной системы сил

Векторная форма условий равновесия сил формулируется следующим

 

 

УРАВНЕНИЯ

 

образом. Для равновесия пространственной системы сил, приложенных к

твердому телу, необходимо и достаточно, чтобы главный вектор системы

сил был равен нулю и главный векторный момент системы относительно

любого центра приведения также был равен нулю.

 

 

Иначе: для того,

чтобы

 

( F1, F2 ,

…, Fn )

0, необходимы

два

условия:

 

 

 

 

 

Д

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R = 0;

МО = 0.

 

(3.1)

Условия (3.1) являются векторными условиями равновесия любой

системы сил. Аналитическая форма условияИравновесия сил

формулируется следующим образом. Для равновесия системы сил,

приложенных к твердому телу, необходимо и достаточно, чтобы модуль

главного вектора системы сил и модуль главного момента этих сил

относительно любого центра были равны нулю.

 

 

156

 

 

 

 

 

2

 

2

2

0;

 

 

 

 

 

 

R Rx

Ry

Rz

 

 

 

(3.2)

 

 

M

M 2 M 2 M 2

0.

 

 

 

 

o

 

 

x

 

y

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Условия (3.2) являются аналитическими условиями равновесия

любой системы сил.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.1.1. Уравнения равновесия пространственной системы сил

Из двух услов й (3.2) равновесия

вытекают шесть

скалярных

уравнен й равновес я (условий равновесия) в виде проекций сил и

записать

 

 

 

 

 

 

 

 

 

 

 

проекц й векторных моментов сил на три оси координат:

 

 

 

 

Rx 0;

 

Ry 0;

Rz 0;

 

 

 

 

 

 

 

 

(3.3)

 

 

М

 

0;

М

 

0;

М

 

 

0.

 

 

 

 

x

y

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б

равновесия

системы сил в

Из (3.3) можно

 

 

 

 

 

уравнения

окончательном в де:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

n

 

 

 

 

n

 

 

 

 

 

А

 

 

Fix

0;

 

 

Fiy

0;

 

Fiz 0 ;

(3.4)

i 1

 

 

 

 

i 1

 

 

 

i 1

 

 

 

n

 

 

 

 

n

 

 

 

n

 

 

 

M x

(Fi )

0;

M y

(Fi )

0;

 

M z (Fi ) 0 .

 

i 1

 

 

 

 

i 1

 

 

 

 

i 1

 

 

 

 

Таким образом, для

равновесия пространственной системы сил,

 

 

 

 

 

 

Д

приложенных к твердому

телу,

необходимо

 

и

достаточно,

чтобы три

суммы проекций всех сил на оси декартовых координат были равны нулю и суммы моментов всех сил относительно трех осей координат также были равны нулю.

Из общих уравнений равновесия для произвольной пространственной системы сил (3.4) получают уравнения равновесияИдля частных систем сил, приложенных к твердому телу.

157

3.1.2. Уравнения равновесия пространственной системы параллельных сил

Направим ось Оz параллельно

силам F1, F2 , …,

Fn (рис. 3.1). Тогда

проекции

параллельных

сил на

С

 

 

перпендикулярные им оси Оx и Oy

будут

равны

нулю,

и

уравнения

n

0;

n

 

0

 

окажутся

F

F

 

i 1 ix

 

i 1

iy

 

 

 

оси

справедл выми

 

для

всех систем

параллельных с

л, т.е.

превратятся в

тождества.

 

 

Оz

 

 

 

Момент

относ тельно

каждой из

параллельных сил равен

нулю,

уравнен е

n

 

тоже выполняется для всех

систем

Мz (F) 0

 

 

 

i 1

 

 

 

 

параллельных

с л.

От расывая

уравнения

равновесия,

которые

выполняютсябтождественно при выбранном направлении оси Оz, и учитывая, что сумма проекций сил на эту ось является алгебраической суммой сил, из (5.13) получаем следующие три уравнения равновесия пространственной системы параллельных сил:

приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю.

 

n

 

n

 

n

 

 

 

 

Fiz 0 ;

M x (Fi ) 0;

M y (Fi ) 0

,

(3.5)

т.е.

i 1

 

i 1

 

i 1

 

 

 

для равновесия пространственной системы параллельных сил,

 

 

А

 

 

 

 

 

 

 

Д

 

3.2. Уравнения равновесия плоской системы сил

относительно этих осей равны нулю, так как ониИпересекают эти оси или параллельны им.

Расположим оси Оx и Oy в плоскости действия сил (рис. 5.5). Так как

ось Oz перпендикулярна силам, то

n

выполняется для всех

Fiz 0

 

i 1

 

плоских систем сил, т.е. является тождеством. Каждая из сил расположена

в одной плоскости с осями координат Оx и Oy

и поэтому ее моменты

158

Таким образом, уравнения равновесия

n

 

 

 

n

 

 

 

 

 

 

 

M x (Fi ) 0;

 

M y (Fi ) 0

 

 

 

 

i 1

 

 

 

i 1

 

 

 

 

 

 

 

для плоской системы сил являются

 

 

 

тождествами. Моменты сил относительно

 

 

 

оси Oz, перпендикулярной силам, равны

 

 

 

алгебраическим моментам

этих

сил

 

 

 

относительно точки О.

 

 

 

 

 

 

 

 

 

 

 

n

 

(Fi )

n

 

 

 

 

 

Так м образом, M z

M o (Fi ) .

 

 

 

три

i 1

 

 

 

 

 

 

 

i

1

 

 

 

 

 

 

 

СИз (3.4) для плоской системы сил после отбрасывания тождеств имеем

уравнен я равновес

я:

 

 

 

 

 

 

 

 

 

n

 

 

 

n

 

 

n

 

 

были

M O

(Fi ) 0 ,

(3.6)

 

 

Fix

0;

Fiy

0;

 

 

i 1

 

 

 

i 1

 

 

i 1

 

 

т.е. для равновес я плоской системы сил, действующих на твердое тело,

необход мо

 

достаточно,

что ы суммы проекций этих сил на каждую из

двух прямоугольных

осей координат, расположенных в плоскости

 

 

 

А

 

действ я с л,

равны нулю и сумма алгебраических моментов сил

относительно любой точки, находящейся в плоскости действия сил, также

была равна нулю.

 

 

 

 

 

 

 

 

 

Для плоской системы параллельных сил одну

 

 

из осей координат, например Оy, можно выбрать

 

 

параллельной

силам

(рис. 3.3). Тогда сумма

 

 

 

 

 

 

 

 

Д

 

проекций параллельных сил на эту ось

 

 

превратится в алгебраическую сумму сил.

 

 

Проекция каждой из сил на ось Оx равна нулю;

 

 

следовательно, сумма проекций сил на ось Оx

 

 

равна нулю, даже если система сил не находится

 

 

в равновесии. Это уравнение является

 

 

тождеством и его следует отбросить.

 

 

 

 

 

Итак, для плоской системы параллельных сил из (3.6) имеем

следующие уравнения равновесия:

 

 

 

 

 

 

 

 

 

 

 

n

 

0;

n

(3.7)

 

 

 

 

 

 

F

M

(F ) 0 ,

 

 

 

 

 

 

i 1

iy

 

ИO i

 

 

 

 

 

 

 

 

i 1

 

 

т.е. для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов относительно

любой точки, находящейся в плоскости сил, также была равна нулю.Из уравнения равновесия плоской системы сил (3.6) можно получить уравнения плоской системы сходящихся сил, для чего за моментную точку

159

надо взять точку пересечения линий действия сходящихся сил. Тогда последнее из уравнений станет тождеством и в качестве уравнений равновесия для плоской системы сходящихся сил останутся только два первых уравнения (3.6).

С

3.3. Распределенные силы

 

распределены силы с

На участке АВ прямой линии длиной l

постоянной нтенс вностью q (рис. 3.4, а).

Заменим эти силы

равнодействующей. Для этого выделим участок dx и определим

этих

 

 

элементарную сосредоточенную силу на этом участке dQ = q dx.

 

Равнодействующая

сил равна сумме, т.е. интегралу от выражения

 

 

Q = l qdx = ql.

(3.8)

 

 

O

 

б

 

Равнодействующая сила Q приложена посередине отрезка в точке С.

Рассмотрим случайАсил, распределенных на отрезке АВ (рис. 3.4, б) по

линейному закону, т.е. по закону треугольной эпюры. Заменим

треугольную эпюру параллельных сил равнодействующей.

ля участка dx

dQ = q dx.

И

 

 

 

 

Интенсивность q в точке, определяемойДкоординатой x, найдем из

подобия треугольников q = qmax x .

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

Тогда равнодействующая треугольной эпюры распределенных сил

равна интегралу

 

 

 

 

 

 

 

 

 

l

l

q

max x dx

=

q

max

l

.

(3.9)

Q = qdx =

 

 

 

 

O

O

 

l

 

 

2

 

 

 

Модуль равнодействующей по формуле (3.9) равен площади эпюры. Точка приложения равнодействующей силы Q проходит через центр тяжести эпюры на расстоянии 2l/3 от вершины треугольника.

160

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности