9.4.5. Силы инерции при равномерном вращении однородного тонкого стержня вокруг неподвижной оси
Однородный тонкий стержень ОА длиной l и массой m прикреплён шарниром О к вертикальной оси y1 , вращающейся с угловой скоростью ,
С |
|
|
|
|
|
|
образуя угол |
с вертикалью (рис. 9.7). |
|
|
и |
|
|
|
|
|
|
|
|
б |
|
|
|
На каждый элементарный участок |
|
|
стержня длиной x и массой mk |
|
|
действует центро ежная сила инерции, |
|
|
равная |
|
|
|
m dx a |
|
m dx 2 x sin , |
|
|
Ф |
m |
k |
a |
k |
k |
|
|
k |
|
|
|
l |
|
l |
Д |
|
|
|
|
|
|
|
|
где x – координата элементарного |
участка стержня dx. |
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
Из полученной формулы видно, что эпюра сил инерции Фk является |
линейной функцией х, |
а равнодействующая Ф этих сил инерции проходит |
через центр тяжести треугольной эпюры, т.е. приложена в точке D на |
расстоянии OD 2l 3 . |
|
|
|
|
|
По модулю равнодействующая сил инерции равна произведению |
массы стержня на ускорение его центра масс: Ф ma m 2 |
l |
sin . |
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы убедиться в том, что сила инерции Ф является |
равнодействующей силой, можно показать, что главный момент |
элементарных |
сил |
инерции Фk стержня относительно точки D равен |
нулю: |
|
|
|
|
|
|
|
|
|
|
|
2l |
|
2 |
|
|
|
|
2 |
|
3 |
|
l |
|
l)cos 0. |
M D (Фk ) Фk |
3 |
l x cos |
Фk (x |
3 |
0 |
|
|
|
2 |
|
|
|
|
|
|
|
3l |
|
|
|
Момент элементарных |
сил |
инерции |
Фk |
относительно центра D |
С |
|
|
|
|
|
|
|
|
представлен в виде двух сумм: первая сумма отрицательная – для сил, расположенных выше точки D, вторая сумма положительная – для сил, расположенных ниже точки D.
Для пр нятых с стем отсчета после замены сумм интегралами
получим |
|
|
|
|
|
|
|
|
и3 |
|
|
|
|
|
|
|
|
2l |
|
|
|
|
M |
|
|
|
3 m |
2 |
|
2l |
|
|
D |
|
|
l |
|
|
3 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
l |
|
m |
dx 2 xsin |
|
|
2l |
|
|
|
|
|
|
|
|
l |
x |
cos . |
|
|
|
|
|
|
2 |
l |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После |
нтегр рован я приходим к выводу о том, |
что главный момент |
сил |
нерц |
стержня |
относительно |
точки |
|
D |
приложения |
|
|
|
А |
|
|
равнодействующей действительно равен нулю: |
M DФ 0 . |
|
|
Рассмотримбдругие возможные случаи приведения сил инерции |
стержня. Пусть тре уется выполнить приведение сил инерции стержня к |
точке О, совпадающей с |
шарниром. |
|
ля |
приведения |
сил инерции |
применим правило параллельного переноса силы. В точку О переносим |
силу Ф из точки D и добавляем к системе пару сил, момент которой равен |
моменту силы Ф относительно точки О: |
M OФ Ф2 H (рис. 9.7,б). |
|
|
|
|
|
|
|
ОА |
|
3 |
|
|
|
В |
данном |
случае |
|
стержень |
находится |
|
в |
динамическом |
|
|
|
|
|
|
|
|
|
|
И |
стационарном равновесии под действием сил mg , |
|
Ф |
и пары сил с |
моментом M OФ. |
|
|
|
Д |
Теперь рассмотрим вращение стержня ОА, точка О которого |
находится |
на расстоянии |
r0 от оси вращения стержня (рис. 9.7,в). |
Равнодействующая трапециевидной эпюры сил инерции стержня проходит |
через центр тяжести трапеции ОАВЕ, координата которого определяется по |
формуле центра тяжести трапеции (10.26) |
раздела «Статика». |
Главный момент сил инерции стержня относительно центра приведения равнодействующей силы равен нулю: M DФ 0 .
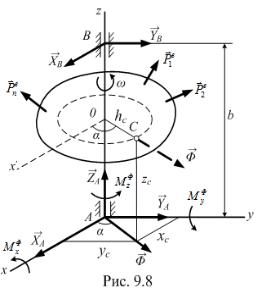
9.4.6. Динамические реакции, действующие на ось вращающегося тела. Динамическое уравновешивание масс
|
Пусть твёрдое тело равномерно вращается с угловой скоростью ω |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вокруг оси, закреплённой в подшипниках А и В (рис. 9.8). |
|
|
YA, |
Найдём динамические реакции ХА, |
|
|
|
|
|
|
|
|
ZA, |
XB, |
|
YВ |
подшипников, |
|
|
|
|
|
|
|
|
действующ е на ось, т. е. реакции, |
|
|
|
|
|
|
|
|
возникающ е при вращении тела. Пусть |
|
|
|
|
|
|
|
|
координатные |
|
|
|
Pe , |
|
|
|
|
|
|
|
|
на тело действуют заданные силы |
|
|
|
|
|
|
|
|
e |
|
e |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
P2 , |
...., |
Pn . |
О означим проекции |
|
|
|
|
|
|
|
|
главного |
вектора |
|
|
эт |
х |
сил |
|
|
на |
|
|
|
|
|
|
|
|
|
|
оси Axyz, |
вращающиеся |
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
вместе с телом, через |
Rxe , |
Rye |
, |
Rze . |
|
|
|
|
|
|
|
|
Главные моменты относ тельно тех же |
|
|
|
|
|
|
|
|
осей обознач м через M xe , M ye , |
M ze . Так |
|
|
|
|
|
|
|
|
как |
тело |
вращается |
равномерно, |
|
то |
|
|
|
|
|
|
|
|
M ze |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения искомых реакций воспользуемся принципом |
Даламбера и, присоединяя к силам, действующим на все точки тела, |
соответствующие силы инерции, составим уравнения (9.12) в проекциях на |
оси Axyz. |
|
|
|
|
|
|
e |
|
|
ДФ |
|
|
В нашем случае этиАуравнения принимают вид |
|
|
|
|
|
|
X A X B |
Rxe |
Фx |
0; |
|
|
|
|
|
|
|
|
|
|
|
Y |
A |
Y |
Re Ф |
y |
0; |
|
Z |
A |
Re Ф |
z |
0; |
(9.18) |
|
|
|
|
|
B |
|
y |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
M e |
|
Ф 0; |
|
|
|
|
И |
|
|
|
Y b |
M |
X |
B |
b M e |
M Ф |
0. |
|
|
|
|
B |
|
|
x |
|
x |
|
|
|
|
|
|
y |
y |
|
|
|
|
|
Последнее |
уравнение M z M z 0 |
удовлетворяется |
тождественно |
|
|
|
|
|
|
|
(так как 0 ) и мы его опускаем. Главный вектор сил инерции Ф mac . |
При |
const |
центр масс С |
имеет |
только нормальное ускорение |
a |
cn |
2h , где |
h – расстояние от точки С до оси вращения. |
|
|
c |
c |
|
|
|
|
|
Следовательно, направление |
вектора Ф совпадает с |
направлением |
ОС. |
|
|
|
|
|
Пунктиром на чертеже показано, как направлен вектор Ф. Если же |
привести силы инерции к некоторому центру, например центру А, то они заменятся приложенной в этом центре силой, равной Ф, и парой, момент которой для центра A слагается из M xФ и M Фy . Вычисляя проекции Ф на
оси координат и учитывая, что |
|
|
|
hc cos xc ; |
hc sin yc , где хс |
и ус – |
координаты центра масс, будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
x |
m 2h cos m 2 x |
c |
; |
|
Ф |
y |
|
m 2h sin m 2 y |
c |
; |
|
|
Ф |
z |
|
0 . |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы найти M xФ |
и |
|
M Фy , |
|
рассмотрим какую-нибудь частицу тела с |
массой mk , отстоящую от оси на расстоянии hk . |
Для неё при const |
сила инерции тоже |
|
|
|
имеет |
|
|
|
только |
центробежную |
|
|
|
|
составляющую |
ФЦ m |
k |
2h , проекц |
|
|
|
|
которой, как и у вектора Ф, равны: |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф m 2 x ; |
|
Ф m 2 y ; |
|
Ф 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражения |
|
ky |
|
|
|
|
|
k |
|
k |
|
|
|
|
kz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kx |
|
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
z |
|
|
|
m |
2 |
y |
|
|
z |
|
|
; |
M |
Ф |
Ф |
|
z |
|
m |
|
|
2 |
x |
|
z |
|
. |
|
СТогда M Ф |
|
|
k |
|
|
|
k |
k |
ky |
kx |
k |
k |
|
|
k |
k |
|
|
|
|
|
|
|
kx |
|
|
|
ky |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оставляя так |
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
для всех точек системы, складывая их и |
вынося общ й множ тель за ско ку, |
|
|
|
|
|
иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
будем |
|
m x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 , |
|
M Ф m y |
k |
z |
k |
2 |
J |
yz |
2 |
|
|
; |
|
|
|
M Ф |
|
k |
|
z |
k |
J |
xz |
(9.19) |
|
x |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где J xz |
|
|
|
J yz |
|
– соответствующие центробежные моменты инерции. |
|
Подставляя все найденные значения в равенства (9.18), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X A X B |
Фx mxc |
2 |
; |
|
YA YB Фy myc |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
(9.20) |
|
|
|
|
Z |
|
|
Ф |
|
|
; |
|
|
X |
|
b M e |
J |
|
2 ; |
|
Y b M e J |
|
|
|
2 |
|
|
|
|
|
|
|
|
A |
|
|
z |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
xz |
|
|
|
|
B |
|
|
|
|
|
x |
|
|
|
yz |
|
|
|
|
|
|
|
|
Уравнения (9.20) и определяют динамические реакции, действующие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
на ось равномерно вращающегося твёрдого тела, если осью вращения |
является ось Oz. Назовём условно статическими реакциями те значения |
реакций, которые дают уравнения |
|
(9.20), если |
в |
|
|
них |
|
положить |
0 |
(статическими, в смысле действующими на ось АВ при покое, эти реакции |
будут, когда проекции на оси Axyz приложенных сил постоянны). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
Как видно из уравнений (9.20), динамические реакции могут вообще |
быть значительно больше статических, причём это зависит не только от |
значения |
ω, |
|
но |
и |
|
|
от |
|
величин |
|
|
хс, |
yс, |
|
J xz , |
|
J yz , характеризующих |
распределение масс тела по отношению к оси вращения z.
Однако из уравнений (9.20) видно, что наличие вращения не будет
влиять на величины реакций подшипников А и В, если |
|
хс = 0; |
yс = 0; |
(9.21) |
J xz 0 ; |
J yz 0 . |
(9.22) |
Равенства (9.21) и (9.22) выражают условия того, что динамические реакции, действующие на ось вращающегося тела, равны статическим
реакциям, т.е. они являются условиями динамической уравновешенности масс
тела при его вращении вокруг оси z.
Условия (9.21) означают, что центр масс тела должен лежать на оси
вращения, а условия (9.22) – что ось вращения должна быть главной осью |
инерции тела для начала координат А. При одновременном выполнении |
условий (9.21) и (9.22) ось Az будет главной центральной осью инерции |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тела. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, динамические реакции, действующие на ось |
вращающегося тела, будут равны статическим, если ось вращения является |
одной |
з главных центральных осей инерции тела. |
Этот вывод остаётся |
справедл вым в случае, когда тело вращается неравномерно. |
|
|
Рассмотренная задача позволяет одновременно уяснить механический |
смысл вел ч н J xz |
|
J yz , а именно: центробежные моменты инерции J xz |
и J yz |
характер зуют степень |
динамической |
неуравновешенности |
масс |
тела |
его вращен |
|
вокруг оси z. |
|
|
|
|
|
|
|
|
|
Динам ческое уравновешивание масс, уравновешивание сил инерции |
представляетприсобою важную техническую задачу, которая сводится к |
определен ю главных центральных осей инерции тела. Любое тело имеет, |
по крайней мере, три взаимно-перпендикулярные главные центральные |
оси инерции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Докажемлюбуюследующее положение: |
ось, проведенную в теле, можно |
сделать главной центральной осью инерции прибавлением к телу двух |
точечных масс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть для тела массой m величины х |
, yс, J |
xz |
, J |
yz |
известны и не |
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
равны нулю. ПрибавимАк телу две массы m1 и m2 в точках с координатами |
(х1, y1, z1) и (х2, y2, z2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда из формул (9.21) и (9.22) следует, что если удовлетворить |
равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mx |
|
m x m |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д0; my m y m y 0; |
(9.23) |
|
|
c |
1 1 |
2 |
|
2 |
|
|
c |
1 |
1 |
2 2 |
|
|
J xz m1x1z1 m2 x2 z2 0; |
|
|
|
|
|
|
|
|
|
|
J yz m1 y1z1 m2 y2 z2 0, |
|
то для полученного тела будет х'с=y'с= J xz' = J yz' |
=0, т. е. Oz станет главной |
центральной осью инерции. |
|
|
|
|
|
|
И |
Подбирая массы m1, m2 и их положения так, чтобы удовлетворялись уравнения (9.23), мы и решим поставленную задачу. Частью величин при этом задаются. Например, можно задать значения m1, m2 и z1, z2 (но так, чтобы было z1 ≠ z2), а x1, y1, x2 , y2 найти из уравнений (9.23) и т. д.
Такой метод уравновешивания масс широко используется в технике для уравновешивания коленчатых валов, кривошипов и т. п. При этом окончательная балансировка производится на специальных стендах.
Для определения давлений на ось в отдельных конкретных задачах обычно не пользуются готовыми уравнениями (9.20), а каждый раз непосредственно применяют принцип Даламбера.
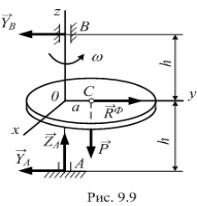
9.5. Динамические реакции вращающегося диска
Ось z вращен я д ска, перпендикулярная к его плоскости (рис. 9.9),
смещена от центра масс на расстояние а. |
Вес д ска равен Р, угловая |
скорость |
С |
|
|
постоянна |
равна ω. |
|
Определ ть |
д намические |
реакции |
подшипн ков А В, если ОА = ОВ = h. |
|
Решен е. Проведём вращающиеся вместе с |
телом |
Oxyz так, |
что ы ось Oy прошла через |
оси |
|
центр масс С д ска (см. рис. 9.9). Ось Oz будет |
главной осью нерц |
по отношению к точке О, |
поскольку плоскость Oxy является плоскостью |
симметрии диска. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
б |
|
|
|
|
|
|
J xz = J yz =0 и из формул (9.19) и условия const вытекает, что |
M 0Ф 0, |
следовательно, |
силы инерции приводятся к одной |
равнодействующей, |
проходящей через точку О и направленной вдоль |
|
|
|
|
АФ |
2 |
линии OС (вдоль оси Oy). По модулю R |
mac |
P |
a . |
g |
Так как силы P и RФ лежат в плоскости Oyz, то реакции |
подшипников лежат в этой же плоскости, |
т. е. имеют составляющие YA , |
|
|
|
|
|
|
|
|
|
|
|
|
И |
ZA в точке А и YB в точке В. ТогдаД, составляя на основании принципа |
Даламбера для всех действующих сил и сил инерции уравнения |
равновесия в проекциях на оси Oy и Oz и уравнение моментов |
относительно центра А, будем иметь |
|
|
|
|
|
|
RФ Y |
A |
–Y 0; |
Z |
A |
– P 0 ; |
Y 2h Pa RФh 0 . |
|
|
|
B |
|
|
|
|
B |
|
|
|
|
|
Решая эти уравнения, получим |
|
|
|
|
|
|
|
|
Y Pa 2 |
a |
P ; |
|
Y |
A |
Pa 2 |
– |
a |
P ; |
|
|
ZA = P . |
|
|
|
|
|
|
|
B |
|
2g |
|
2h |
|
|
|
2g |
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реакции YA и YB всё время располагаются в плоскости Oyz, вращающейся вместе с телом.

Интегрированием можно превратить кинематические связи в геометрические. Все геометрические и интегрируемые кинематические связи называют голономными. Неинтегрируемые кинематические связи, которые нельзя свести к геометрическим, являются неголономными.
В дальнейшем изложении неголономные связи не рассматриваются. |
При движении механической системы координаты точек и их |
С |
|
производные по времени, входящие в уравнения связей, могут зависеть от |
времени. Кроме того, в уравнения связей время может входить явно, |
помимо коорд нат |
х производных. Связи, в уравнения которых время |
явно не вход т, называются стационарными или склерономными. Если время |
входит явно в уравнен е связи, то связь называется нестационарной или реономной. Нестац онарные связи обычно реализуются посредством движущ хся ли деформ рующихся тел.
В простейшем случае одной точки нестационарная геометрическая удерживающая связь в форме движущейся или деформируемой поверхности меет уравнение f(x, у, z, t) = 0.
называют неосво ождающими или двусторонними, если они |
Связи |
|
или |
выражаются математ ческими равенствами, и освобождающими |
б |
|
односторонн ми, если они выражаются неравенствами. |
|
Для одной точки М1 (рис. 10.1), |
|
скрепленной с концом жесткого стержня, |
|
другой конец которого закреплен в |
|
неподвижной |
точке |
О, |
уравнение |
|
неосвобождающей |
|
|
голономной |
|
|
|
|
|
Д |
|
стационарной геометрической связи имеет |
|
вид |
|
А |
|
x 2+у 2 |
+z 2 l 2=0, |
|
|
где l длина стержня. |
|
|
Если стержень заменить нитью, например, для точки М2 |
такой же |
длины, то связь (нить) будет освобождающей. |
И |
|
|
Если при движении точка М2 окажется от точки О на расстоянии, меньшем длины нити, то нить уже не стесняет свободу перемещения точки. Уравнение неудерживающей односторонней голономной связи
имеет вид |
|
x 2 + у 2 + z 2 l 2 ≤ 0. |
(10.3) |
Связь (10.3) является односторонней. Она обеспечивает движение точки по сфере радиуса l и внутри сферы по сферическим поверхностям
меньшего радиуса. Удерживающая связь типа z b = 0 обеспечивает движение точки в плоскости. Связь, представленная уравнением z b ≤ 0, является неудерживающей. Она обеспечивает движение точки в плоскости и под плоскостью (между параллельными плоскостями).

10.2. Возможные перемещения
Возможными, или виртуальными, перемещениями несвободной механической системы называются воображаемые бесконечно малые
перемещения, допускаемые в данный момент наложенными на систему связями.
Возможным является любое воображаемое бесконечно малое перемещение, которое происходит при фиксированном значении времени
как бы мгновенно, обозначается оно s в отличие от действительного |
перемещен я |
ds , про сходящего |
под действием приложенных сил за |
малый промежуток времени dt. |
Возможное перемещение |
называется |
(рис. 10.2). |
|
|
вариац ей, действ тельное – дифференциалом. Поскольку возможные |
Сперемещен я – бесконечно малые величины, то криволинейные |
перемещен я |
заменяют прямолинейными направленными |
отрезками, |
отложенными по касательным к траекториям точек; длины этих отрезков вычисляют как дл ны дуг δs=Rδφ. Рассмотрим возможные перемещения точек рычага АВ, закреплённого в точке О цилиндрическим шарниром
|
Стержень |
АВ меет одну степень |
свободы, его возможным перемещением |
является |
малый |
поворот на |
угол δφ бесконечновокруг точки О в плоскости, |
перпендикулярной оси вращения. |
|
Концы стержня – точки |
и В – должны перемещаться по дугам |
|
|
|
|
АА, |
ВВ. Так как эти дуги – величины бесконечно малые, то их заменяют |
прямолинейными, направленными по касательным к траекториям точек |
векторами sA , |
А |
sB ; модули векторов вычисляют как длины дуг (рис. |
10.2): δsА=OA·δφ; sB =OB·δφ. |
|
|
В данном примере sA , |
sB – возможные линейные перемещения |
точек; δφ – возможное угловое перемещение системы. |
|
|
|
Д |
10.3. Элементарная работа силы на возможном перемещении. Идеальные связи
Элементарную работу силы на возможном перемещении ее точки |
приложения вычисляют по обычным формуламИдля элементарной работы, |
например δA= F r =Fxδx+Fyδy+Fzδz и другим. |
|
Для механической системы, состоящей из п точек, к которым |
приложены силы, элементарная работа этих сил на каком-либо возможном |
перемещении системы соответственно выразится так: |
|
п |
(10.4) |
А Fk rk . |
k 1 |
|
Элементарная работа сил при этом зависит от выбора возможного перемещения системы. Обозначим силы реакций связей для точек системы
Rk .
Идеальными называют связи, у которых сумма элементарных работ сил реакций на любых возможных перемещениях равна нулю:
п |
|
Rk rk 0. |
(10.5) |
k 1 |
|
Рассмотрим примеры идеальных связей. |
|
1. В абсолютно твердом теле точки связаны идеальными связями, под |
которыми можно пон мать идеальные невесомые стержни. |
|
лами реакц й связей в этом случае являются внутренние силы, для |
Скоторых было доказано, что сумма элементарных работ этих сил на любых |
элементарных перемещениях точек тела равна нулю. |
|
Силы2. Абсолютно гладкая поверхность, или абсолютно гладкая линия, является деальнойбсвязью для точки. Возможные перемещения точки с такими связями направлены по касательным к поверхности или линии.
реакц в эт х случаях направлены по нормалям к ним, т.е. перпенд кулярны с лам. Так, например, все шарниры (поверхности) без трения, подв жные неподвижные, являются связями, идеальными для тел, соединенных такимиАсвязями. Шарниры без трения, как связи идеальные, эквивалентны связям между точками в твердом теле.
3. Гибкие нерастяжимые связи типа нитей, канатов, тросов и т.п., соединяющих точки системы, являются связями идеальными. В каждом сечении такой связи силы реакций (силы натяжения) равны по модулю и противоположны по направлениюД, а возможные перемещения у точек приложения сил одни и те же. Сумма элементарных работ сил натяжений для любых сечений таких связей равна нулю.
В принципе возможных перемещений существует прием,
позволяющий |
неидеальные |
связи превращать в |
идеальные. Например, |
реакцию Rk |
|
|
|
|
|
|
И |
шероховатой поверхности можно разложить на нормальную и |
касательную составляющие: |
Rk |
Nk Fk . |
|
|
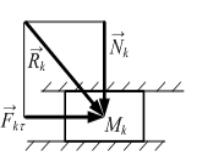
Шероховатая поверхность накладывает на |
|
точку или тело две связи (рис. 10.3). Нормальная |
|
связь Nk является идеальной, а неидеальную |
|
касательную составляющую Fk переводят в |
|
разряд задаваемых сил и вычисляют через |
|
реакцию |
нормальной |
|
идеальной |
связи: |
|
Fk fNk . |
|
Таким |
образом, |
|
реальная |
|
шероховатая |
неидеальная |
поверхность |
Рис. 10.3 |
превращается в идеальную связь. |
|
|
|
|








