
2192
.pdf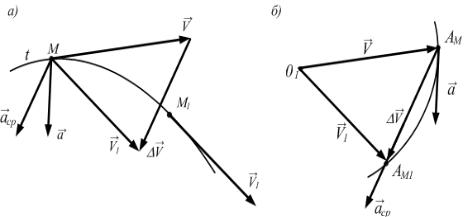
4.2.2. Ускорение точки
Пусть движущаяся точка М в момент времени t имеет скорость V . В
момент времени t1 t t эта точка занимает положение М1, имея |
|
скорость V (рис. 4.8,а). |
|
1 |
|
С |
|
приращениеЧтобы ть |
скорости V за время ∆t, перенесём |
зобразa . |
|
Рис. 4.8 |
|
вектор скорости V1 параллельно самому себе в точку М.
Средн м ускорен ем точки аср |
за время ∆t называют отношение |
||
А |
|||
|
|
V |
|
|
ср |
t |
|
Среднее ускорение точки параллельно приращению скорости V . Среднее ускорение не имеет на траектории конкретной точки приложения и изображено в точке М условно. В общем случае среднее ускорение зависит от ∆t.
Ускорением точки a в момент времени t называют предел, к которому стремится среднее ускорение при ∆t, стремящемся к нулю, т.е.
a |
lim |
V |
dV . |
|
t 0 |
t |
dt |
|
Д |
||
Таким образом, ускорение точки равно первой производной по времени |
|||
от скорости точки. Приращение скорости ∆V и, следовательно, среднее |
|||
ускорение aср направлено в |
сторону |
вогнутости траектории. Так же |
|
направлены и их предельные значения при ∆Иt, стремящемся к нулю. Поэтому ускорение точки направлено тоже в сторону вогнутости траектории. Кроме того, ускорение как первая производная по времени от скорости, по свойству годографа вектора, имеет направление, параллельное касательной к годографу вектора скорости (рис. 4.8,б). Скорость точки направлена по касательной к траектории и вычисляется, согласно её определению, по формуле
171

|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
. |
|
|
(4.9) |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для ускорения точки соответственно имеем |
|
|||||||||||||||||
С |
|
|
|
|
|
dV |
|
|
d 2r |
|
|
|||||||
|
|
|
|
a |
dt |
|
dt2 . |
|
(4.10) |
|||||||||
Таким образом, если движение точки задано векторным способом, то |
||||||||||||||||||
скорость и ускорение вычисляют по формулам (4.9) и (4.10). Определение |
||||||||||||||||||
скорости |
ускорен |
я точки сводится к математической задаче вычисления |
||||||||||||||||
первой |
второй про зводных по времени от радиуса-вектора этой точки. |
|||||||||||||||||
Для практ ческого выч сления скорости и ускорения обычно используют |
||||||||||||||||||
кинемат |
способы |
задания движения. Векторный |
||||||||||||||||
координатный |
|
|
естественный |
|||||||||||||||
способ вв ду его компактности удобен для теоретического изложения |
||||||||||||||||||
|
ки точки, напр мер при доказательстве теорем. |
|
||||||||||||||||
|
|
б |
|
|
|
|||||||||||||
4.3. Скорость |
|
ускорение точки при координатном способе |
||||||||||||||||
|
|
|
|
|
|
|
|
|
задания движения |
|
|
|||||||
|
|
4.3.1. Скорость точки в декартовых координатах |
|
|||||||||||||||
Разлож в |
рад ус-вектор |
и скорость точки на составляющие, |
||||||||||||||||
|
|
|
|
|
|
|
А |
|
||||||||||
параллельные осям координат (рис. 4.9), получим |
|
|||||||||||||||||
|
|
|
|
|
r xi yj zk; |
|
|
V Vxi Vy j Vz k , |
(4.11) |
|||||||||
где х, у, |
z |
– |
координаты точки |
М; |
|
i , j,k |
– |
единичные векторы |
осей |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||
координат; Vx,Vy, Vz – проекции скорости на оси координат. |
|
|||||||||||||||||
Учитывая |
|
|
|
(4.11), |
|
согласно |
|
|
|
|||||||||
определению скорости, имеем |
|
|
|
|
|
|
|
|
|
|||||||||
|
dr |
d |
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
V |
|
|
|
|
(xi |
yj |
zk) xi |
yj |
zk, |
|
||||||||
dt |
dt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
(4.12) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
здесь i , j, k |
не изменяются при движении |
|
|
|
||||||||||||||
точки М. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точки над х, у, z означают их |
|
|
|
|||||||||||||||
производные по времени. Сравнивая (4.11) |
|
|
|
|||||||||||||||
и (4.12), получаем для проекции скорости |
|
|
|
|||||||||||||||
на декартовы оси координат следующие |
|
|
|
|||||||||||||||
формулы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx |
|
dх |
|
х; Vy |
dy |
y; |
Vz |
dz z. |
(4.13) |
||||
|
|
|
|
|
dt |
|||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
dt |
|
||
172

Проекция вектора скорости на какую-либо координатную ось равна первой производной по времени от соответствующей координаты движущейся точки.
По проекциям определяют модуль скорости и направляющие
косинусы углов вектора скорости с осями координат: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
V |
x |
|
|
|
|
|
|
Vy |
|
|
||||||||||||
V |
Vx2 |
Vy2 |
Vz2 |
x2 y2 z2 |
; |
cos(V,i ) |
|
; |
|
|
cos(V, |
j) |
|
; |
|
||||||||||||||||||
|
|
|
V |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(V,k ) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
оси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
то, |
выбрав |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Если точка дв жется в плоскости, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
коорд нат Оx |
|
Оy в этой плоскости, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
z const 0; |
|
Vz z |
0; |
Vy |
y |
; Vx x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
2 |
Соответственно |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
x |
|
y |
|
; cos(V |
,i ) V |
; |
cos(V |
, j) V . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
||||||||||||||||||
Для прямолинейного движения точки координатную ось, например |
|||||||||||||||||||||||||||||||||
Оx, направляют по траектории (рис. 4.10). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Тогда |
y const 0 |
и |
z const 0 , |
следовательно, |
y 0; |
z 0 . |
|||||||||||||||||||||||||||
Координату точки, проекцию скорости и ее модуль определяют по |
|||||||||||||||||||||||||||||||||
формулам x f (t); |
|
Vx |
x ; |
V Vx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
4.3.2. Уравнение годографа вектора скорости |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Пусть известны уравнения движения точки в декартовых |
|||||||||||||||||||||||||||||||||
координатах. |
На |
рис. |
4.7,а |
показаны траектория |
точки |
и |
несколько |
||||||||||||||||||||||||||
векторов скорости для |
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||||||
разных моментов времени, а на рис. 4.7,б показан |
|||||||||||||||||||||||||||||||||
годограф вектора скорости движения точки.
Точке М (x, y, z) на траектории соответствует точка АM (Vx ,Vy ,Vz ) на
годографе вектора скорости.
Координаты точки АM , согласно определению годографа, выражают через проекции скорости на ортогональные оси координат О Vx , Vy , Vz
V Vxi Vy j Vz k , где Vx (t) x ; Vy (t) y ; Vz (t) z .
Представленные выражения проекций вектора скорости являются параметрическими уравнениями годографа вектора скорости.
173
4.3.3. Ускорение точки в декартовых координатах
Вектор ускорения точки представим через его проекции на оси декартовой системы координат.
С |
|
|
|
|
|
|
|
а ахi ay j az k , |
|
|
|
|
|
|
|
|
(4.14) |
|||||||||||||||
где ах, ау, аz – проекции вектора ускорения на координатные оси. |
||||||||||||||||||||||||||||||||
огласно определению ускорения и формулам (4.11) и (4.12), имеем |
||||||||||||||||||||||||||||||||
|
|
|
dV |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а |
|
|
|
|
|
|
(Vxi |
Vy j |
Vz k ) |
xi yj |
zk. |
|
|
(4.15) |
|||||||||||||||||
dt |
dt |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
равн вая (4.14) и (4.15), получаем формулы для проекций |
||||||||||||||||||||||||||||||||
движущейся |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ускорен я на оси декартовой системы координат: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ах |
dV |
x |
x; |
|
|
|
|
ау |
|
dVy |
y ; |
|
|
аz |
|
dV |
z |
z. |
(4.16) |
|||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||
б |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Проекц вектора ускорения на какую-либо координатную ось равна |
||||||||||||||||||||||||||||||||
второй про зводной по времени от соответствующей |
координаты |
|||||||||||||||||||||||||||||||
точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ч словое значен е ускорения и косинусы углов вектора ускорения с |
||||||||||||||||||||||||||||||||
осями коорд нат определяют по формулам |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
а |
|
|
А |
|
|
|
|
|
|||||||||||||||||||||||
а |
|
|
а |
2 |
а |
2 |
|
а2 |
|
x2 |
y2 |
|
z2 ; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
х |
|
|
|
у |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
|
|
|
|
|
|
|
|
|
|
|
ay |
|
|
|
|
|
|
|
a |
z |
|
(4.17) |
|||||
cos(a,i ) |
|
a |
; |
|
|
|
cos(a, |
|
j) |
|
|
a |
; |
|
cos(a, k ) |
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||||
При движении точки в плоскости оси Оx и Оy выбирают в этой же |
||||||||||||||||||||||||||||||||
плоскости. Тогда z=const=0; аz |
z 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Формулы для ускорения и его проекций на оси координат примут вид |
||||||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
yj; |
|
|
а |
х |
х; |
|
ау у. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||||||||||
|
|
|
|
|
а |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|||||
Соответственно |
х |
|
|
у |
; |
|
|
cos(a,i ) a |
; cos(a, j) |
a . |
||||||||||||||||||||||
Для прямолинейного движения ось Оx направим по траектории точки. |
||||||||||||||||||||||||||||||||
Тогда у = const = 0; |
|
z = const = 0 и |
|
|
ау |
у 0 |
; тогда |
a x . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4. Скорость и ускорение точки при естественном способе задания движения
4.4.1. Скорость точки
Пусть движение точки задано естественным способом, т.е. уравнением s f t . Вычислим скорость точки. Для этого используем
радиус-вектор r движущейся точки, начало которого находится в
174

неподвижной точке О1 (рис. 4.11). При движении точки её радиус-вектор
изменяется с течением времени и, следовательно, является функцией двух переменных r s,t .
Определим скорость точки, используя правило дифференцирования функций с двумя переменными.
V ddtr ddsr dsdt ddsr s s V . (4.18)
и |
|
||
С |
|
dr |
|
Касательный вектор |
|
ds |
, равный производной от радиуса-вектора |
по дуговой коорд нате, направлен по касательной к кривой в точке М. |
||||||||||
считать проекциейалгебраическойскорости на положительное направление касательной к |
||||||||||
Модуль этого вектора равен единице, как предел отношения длины |
||||||||||
хорды r |
к дл не стяг вающей дуги s при стремлении её к нулю. |
|
|
|||||||
|
|
|
|
всегда направлен по касательной к траектории в |
||||||
Ед н чный вектор |
||||||||||
сторону возрастан я дуговой координаты независимо от направления |
||||||||||
движен я точки. |
|
|
|
|
|
|
. Её можно |
|||
Величина V s называется |
|
|
скоростью точки |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
траектории, совпадающее с направлением единичного вектора . |
|
|
||||||||
Модуль скорости точки в данный момент времени равен первой |
||||||||||
производной от дуговой координаты |
точки по времени: |
|
|
|
||||||
|
|
|
|
|
ds |
|
|
|
|
(4.19) |
|
|
|
АV s. |
|
|
|||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
4.4.2. Вектор кривизны. Радиус кривизны |
|
|
|
|||||
В точке М кривой |
линии |
проведём |
|
|
|
|
||||
касательную (рис. 4.12). |
|
Д |
|
|||||||
В другой близкой точке кривой М1, |
И |
|||||||||
отстоящей |
от точки М на расстоянии s , |
|||||||||
построим |
касательную |
1 . Единичный |
||||||||
|
|
|
|
|
|
|
||||
вектор характеризует в разных точках |
||||||||||
линии направление касательной, которое |
||||||||||
оценивают изменением угла между двумя |
|
|
|
|
||||||
касательными на отрезке дуги. |
|
|
|
|
|
|
||||
По определению, вектором |
кривизны |
K кривой является |
предел |
|||||||
отношения |
|
|
|
|
|
|
|
|
|
|
175
|
|
|
|
K lim |
d . |
(4.20) |
|||
|
|
|
|
|
s 0 |
s |
ds |
|
|
На рис. 4.12 в точках и M1 показаны касательные векторы, модули |
|||||||||
которых равны |
1. Для оценки величины изменения вектора |
на |
|||||||
дуге s |
|
|
|
1 |
|
|
|
|
|
вектор 1 |
перенесём в точку М.Тогда из векторного треугольника |
||||||||
|
|
|
|
В свою очередь, |
можно выразить |
через ∆φ из |
|||
МАВ 1 |
. |
||||||||
треугольника МАВ: 1 . Таким образом, модуль вектора кривизны |
|||||||||
из (4.20) равен |
|
K . |
|
|
|
||||
|
|
|
|
|
(4.21) |
||||
нормали |
s |
|
|
|
|
||||
СК касательным векторам , |
|
|
|
|
|||||
1 на рис. 4.12 в точках М, |
М1 проведены |
||||||||
|
в в де отрезков , |
1, которые пересекаются в точке О1, |
|||||||
называемой |
центром кр визны дуги ММ1. Величины , |
1 являются |
|||||||
|
|
б |
|
|
|
||||
радиусами кр в зны в точках М, М1. |
|
|
|
|
|||||
Используя формулы геометрии и учитывая, что при s 0 ; 1 |
, |
||||||||
получим |
|
s . Тогда из выражения |
(4.21) найдём K 1 , где |
– |
|||||
|
|
|
|
|
|
|
|
|
|
радиус кривизны траектории.
Модуль вектора кривизны К есть величина, обратная радиусу кривизны
(радиусу |
кривой) |
в данной точке. Направление вектора K |
определяет |
||
вектор, который в пределе при ∆φ→0 совпадает с нормалью n . |
|
||||
Из формулы (4.20) получим окончательно |
|
||||
|
|
|
|
1 |
(4.22) |
|
|
АK n . |
|||
|
|
|
|
|
|
|
|
4.5. Естественный трёхгранник |
|
||
|
|
|
|
И |
|
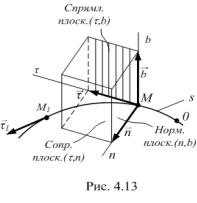
Для определения понятия соприкасающейся |
|
||||
плоскости проведем вспомогательнуюДплоскость |
|||||
через две пересекающиеся прямые M |
и M1 1 |
|
|||
(рис. 4.13). Предельное положение этой |
|
||||
плоскости при совпадении в пределе точки М1 с |
|
||||
точкой |
М |
называют |
соприкасающейся |
|
|
плоскостью кривой в точке М. В случае плоской кривой соприкасающейся плоскостью для всех точек кривой является сама плоскость, в которой расположена эта кривая.
Построим в точке М кривой линии естественные оси координат. Первой естественной осью является касательная . Положительное направление этой оси совпадает с направлением единичного вектора касательной ,
176
направленного в сторону возрастания дуги. Перпендикулярно касательной оси располагается нормальная ось n , направленная в сторону вогнутости кривой – к центру кривизны.
Оси и n образуют соприкасающуюся плоскость, которая находится в плоскости кривой ММ1 , т.е. в плоскости, образованной векторами , 1 ,
при ММ1 0 . Через ось n перпендикулярно оси проходит нормальная плоскость, в которой перпендикулярно осям и n расположена вторая
нормаль b, называемая бинормалью. Три взаимно-перпендикулярные оси |
|||||||||||
, n , b, полож тельные направления которых совпадают с направлениями |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
единичных векторов |
, n , b , называют естественными осями координат. |
||||||||||
точки |
|
|
|
|
|
|
|||||
Эти оси образуют в точке М естественный трёхгранник. При движении |
|||||||||||
СМ по кр вой естественный трёхгранник движется вместе с точкой |
|||||||||||
как твёрдое тело, поворачиваясь вокруг вершины, совпадающей с |
|||||||||||
движущейся точкой. |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|||||||||
На р с. 4.13 представлена правая естественная система координат. |
|||||||||||
Правило определен я правой системы координат заключается в том, |
|||||||||||
чтобы, смотря навстречу вектору |
b , |
видеть поворот вектора к вектору n |
|||||||||
против вращен я часовой стрелки. Термин правая система координат |
|||||||||||
заимствован |
з ф з ки: вправо происходит вращение буравчика, |
остриё |
|||||||||
|
А |
|
|||||||||
которого совпадает с вектором b |
|
при повороте оси к оси n . |
|
||||||||
4.6. Ускорение точки при криволинейном движении |
|
||||||||||
Скорость точки при задании ее движения естественным способом |
|||||||||||
определяют |
выражением |
(4.18) |
|
как произведение модуля скорости и |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
единичного касательного вектора V V . |
|
|
|||||||||
Вектор ускорения a точки, |
согласно определению, есть производная |
||||||||||
от выражения вектора скорости по времени t . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
И |
|
При определении производной от произведения учитываем, что |
есть |
||||||||||
сложная функция двух переменныхД: s,t . |
|
||||||||||
|
|
|
|
d |
|
|
|
dV |
|
|
|
|
dV |
|
|
|
d ds |
|
|||||
|
a |
dt |
|
dt |
V |
dt |
V |
ds dt . |
(4.23) |
||
В соответствии с полученными ранее выражениями (4.19), (4.20), |
|||||||||||
(4.22) запишем |
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
V |
|
|
(4.24) |
||||
|
a |
a |
|
n |
a ann . |
||||||
|
|
|
|
|
|
|
|
|
|
||
Получено разложение ускорения точки по естественным осям координат. Часть ускорения a называют касательной составляющей
ускорения. Другую часть an называют нормальной составляющей ускорения.
177
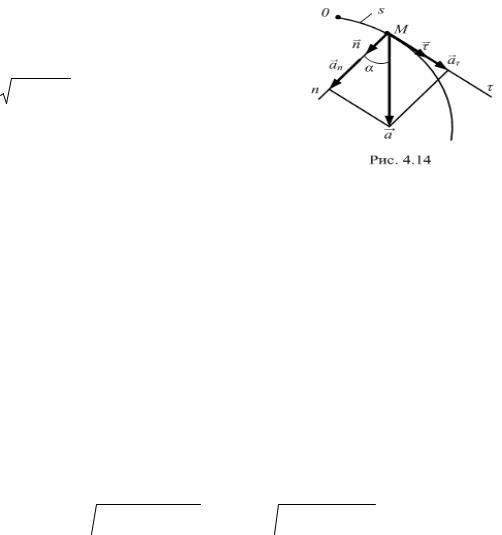
Она направлена в сторону вогнутости траектории, т. е. в сторону единичного вектора главной нормали n .
Таким образом, ускорение точки при криволинейном движении
|
|
|
|
|
a a an . |
|
|
|
|
(4.25) |
|||
Из выражения (4.25) получим формулы для проекций ускорения на |
|||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
||
естественные оси: |
|
|
|
|
|
|
V 2 |
|
|
|
|
|
|
|
|
a |
|
dV |
; |
an |
; |
|
ab 0 . |
(4.26) |
|||
|
|
|
|
dt |
|
|
|
|
|
|
|
направление касательной, |
|
Проекц ю ускорен я на положительное |
|||||||||||||
нормали |
|
|
|
|
|
|
|
|
|||||
совпадающую с направлением единичного вектора , называют |
|||||||||||||
касательным ускорен ем, а на главную нормаль, направленную по |
|||||||||||||
единичному вектору n , – нормальным ускорением. Проекция ускорения на |
|||||||||||||
бинормаль, направленная по единичному вектору b , равна нулю; |
|||||||||||||
бa |
|
|
|
|
|||||||||
следовательно, ускорен е точки расположено в соприкасающейся |
|||||||||||||
плоскости траектор . В этой плоскости находятся единичные векторы |
|||||||||||||
касательной |
главной |
|
|
. |
|
|
|
|
|
|
|
|
|
Уч тывая ортогональность векторов a |
и an |
|
|||||||||||
(рис. 4.14), |
в соответств и с уравнением (4.25) |
|
|||||||||||
|
|
А |
|
||||||||||
имеем полное ускорение точки |
|
|
|
|
|
|
|
|
|||||
a |
a2 an2 ; |
|
tg |
|
. |
|
|
(4.27) |
|
||||
|
|
|
|
|
|
an |
an |
|
|
|
|
|
|
Нормальная составляющая ускорения |
всегда |
|
|||||||||||
|
|
|
|
|
|
Д |
|||||||
направлена в сторону вогнутости траектории. |
|
|
|||||||||||
Касательная составляющая a при s 0 направлена в положительную |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сторону касательной, т. |
е. |
по направлению единичного вектора , а при |
|||||||||||
s 0 – в отрицательную, противоположно . |
|
|
|||||||||||
|
|
s 0 |
векторы скорости |
|
и касательной |
составляющей |
|||||||
При s 0 и |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
И |
|
ускорения направлены в одну сторону – по |
вижение точки является |
||||||||||||
ускоренным в положительном направлении касательной к траектории. |
|||||||||||||
При s 0 и |
s 0 |
векторы |
скорости |
|
и касательной |
составляющей |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ускорения также имеют одинаковые направления, и, следовательно, движение точки является ускоренным в отрицательном направлении по касательной к траектории.
При s 0 |
и |
s 0 имеем замедленное движение точки в |
|
|
|
отрицательную сторону по касательной к траектории точки.
В том случае, если требуется определить касательное и нормальное ускорения при координатном способе задания движения точки, то сначала по формулам (4.13) и (4.17) определяют модули скорости и ускорения точки:
V  Vx2 Vy2 Vz2 ; a
Vx2 Vy2 Vz2 ; a 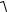 ax2 a2y az2 .
ax2 a2y az2 .
178

|
|
|
|
|
|
2Vx |
dVx |
|
|
dVy |
dVz |
|
|
|
|
|
dV |
|
dt |
2Vy |
|
2Vz dt |
|
||
Согласно формуле (4.26), |
a |
|
dt |
|||||||||
dt |
|
2 |
Vx2 Vy2 Vz2 |
|||||||||
или |
a |
Vxax |
Vy ay Vz az |
. |
|
(4.28) |
||||||
|
|
|
|
|
|
|
||||||
С |
|
|
|
|
|
V |
|
|
|
|
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак плюс, полученный в ответе после вычисления дроби, соответствует ускоренному движению точки, а знак минус – замедленному. Нормальное ускорение точки определяют из формулы
(4.25): an a2 |
a2 . |
|
|
|
|
|
траектории |
|
an . |
||||
Рад ус кр в зны |
|
|
находим из формулы (4.26) |
|||
4.7. Класс ф кац я движений точки по ускорениям её движения |
||||||
Выясн м |
зав с мость |
характера движения от значений её |
||||
нормального |
касательного ускорений в течение некоторого промежутка |
|||||
времени. |
|
|
|
|
|
|
Случай 1. an 0 ; a 0 . Точка движется прямолинейно и равномерно. |
||||||
|
|
|
|
|
|
|
|
б |
|
||||
Случай 2. |
an 0 ; |
a 0 . |
Точка движется криволинейно и равномерно. |
|||
Модуль её ускорения |
a an V 2 . Если a 0 в отдельный момент |
|||||
модуль её скорости Аимеет экстремальное значение. Например, при колебаниях маятника его скорость максимальна в вертикальном
времени, то точка не движется равномерно, а в этот момент времени
положении маятника. При экстремуме скорости ускорение в этом положении маятника a 0 .
Случай 3. an 0 ; a 0 . Точка движется прямолинейно и неравномерно.
|
|
2 |
|
2 |
|
|
|
Дd s V |
|||||
Модуль её ускорения |
a a |
dt2 |
. Если an |
|
0 |
в некоторый |
|
|
|
|
|
||
момент времени, то точка не движется прямолинейно, а проходит точку перегиба траектории или модуль её скорости обращается в нуль
(например, при изменении направления движения точки |
V 0 ), |
в этой |
|||||
точке скорость меняет знак. |
|
|
И |
||||
Случай |
4. |
an 0 ; |
a 0 . |
Точка |
совершает |
криволинейное |
|
неравномерное |
движение. |
Модуль |
её ускорения a |
a2 an2 . |
Если |
||
направления |
векторов V и |
a совпадают, |
то движение |
ускоренное, в |
|||
противном случае – замедленное.
179
4.7.1. Равномерное движение
Равномерным называют такое движение точки по траектории любой формы, при котором численная величина скорости всё время остаётся
постоянной: V const . Тогда |
a dV 0 , |
и ускорение точки равно его |
||||||||||||||||
С |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|||||
нормальному ускорению a an |
V 2 |
. Найдём уравнение равномерного |
||||||||||||||||
кривол нейного дв жен я. Из формулы V ds |
получаем ds Vdt . Пусть |
|||||||||||||||||
в начальный момент времени |
t0 |
0 |
|
|
|
dt |
|
|
|
|
|
|||||||
точка находится от начала отсчёта на |
||||||||||||||||||
точки s s0 |
Vt . |
|
|
|
|
|
|
(4.29) |
||||||||||
расстоян |
s0 |
. Тогда, взяв от левой и правой частей равенства |
||||||||||||||||
определённые |
нтегралы |
в |
соответствующих |
пределах, |
получим |
|||||||||||||
s |
t |
|
|
s s0 Vt . Так как V const , окончательно находим закон |
||||||||||||||
ds Vdt |
ли |
|||||||||||||||||
s0 |
0 |
|
б |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
равномерного дв жен я |
в виде |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
А |
|
|
|
|||||||||||
|
|
|
|
4.7.2. Равнопеременное движение |
|
|
|
|||||||||||
|
Равнопеременным называют такое движение точки по траектории |
|||||||||||||||||
любой формы, при котором касательное ускорение остаётся постоянным: |
||||||||||||||||||
a |
const . |
Найдём закон этого движения, |
считая, |
что при t0 |
0 |
s s0 ; |
||||||||||||
V V0 , |
|
V0 |
|
|
|
|
Дds |
|
||||||||||
где |
– начальная скорость точки. |
Согласно |
формуле |
(4.26), |
||||||||||||||
dV a |
, или |
dV a dt . Так как |
a const , |
то, |
взяв |
от обеих |
частей |
|||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
последнего равенства интегралы в соответствующих пределах, получим |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
|
|
|
|
|
V V0 |
a t . |
|
|
|
|
|
|
(4.30) |
|||||
|
Формулу (4.30) представим в виде |
dt |
V0 |
a t или ds V0dt a tdt . |
||||||||||||||
Вторично интегрируя, найдём уравнение равнопеременного движения |
||||||||||||||||||
точки: |
|
|
|
|
|
|
|
|
|
a t2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
s s |
0 |
V t |
|
|
. |
|
|
|
|
(4.31) |
||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если при движении точки модуль скорости возрастает, то движение |
|||||||||||||||||
называется равноускоренным a |
0 , а если убывает – равнозамедленным |
|||||||||||||||||
a |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данное утверждение справедливо при движении точки в положительном направлении отсчёта дуговой координаты s .
180
