
2192
.pdf
Таким образом, элементарная работа |
|
||
силы, приложенной в какой-либо точке |
|
||
твердого тела, в общем случае движения |
|
||
складывается из элементарной работы на |
|
||
элементарном |
поступательном |
перемещении |
|
вместе с какой-либо точкой тела и на |
|
||
элементарном |
вращательном |
перемещении |
|
вокруг этой точки. В случае вращения |
|
||
твердого тела вокруг неподвижной точки, |
|
||
выбрав эту точку за полюс О, по (8.17) для |
|
||
элементарной работы меем |
|
|
|
перпендплоскостикулярна движения и проходит через произвольную |
|||
С dA =Mω( F )dφ. |
(8.18) |
||
Поворот на угол dφ следует рассматривать в каждый момент времени |
|||
вокруг своей мгновенной оси вращения. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
работы |
|
|
|
|
|
|
|
|||||||||||
Формулу (8.17) пр меняют и для плоского движения твердого тела, |
||||||||||||||||||||
только в этом случае мгновенная |
ось |
относительного |
вращения |
|||||||||||||||||
точку тела. |
|
|
|
|
|
|
|
|
|
|
|
системы сил ( F1, F2 ,..., Fn ) для |
||||||||
При |
действ |
|
|
на |
твердое |
тело |
||||||||||||||
элементарной |
|
|
|
силы Fk , согласно полученным формулам, имеем |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (Fk )d . |
|
||||
|
dAk Fk dr0 |
M0 (Fk ) dt |
Fk dr0 |
|
||||||||||||||||
Элементарная ра ота системы сил |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||
|
|
dA |
|
n |
dA |
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
0 |
|
|
|
0 |
k |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1Аk 1 k 1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M d , |
|
|
|
|
||||
|
|
R dr |
M0 dt |
R dr0 |
|
|
|
|
||||||||||||
где |
|
|
|
n |
|
|
|
|
|
n |
|
|
|
M |
|
n |
|
|
||
|
R |
|
Fk ; |
|
M 0 |
|
M 0 |
(Fk ) ; |
|
M (Fk ) |
|
|||||||||
|
|
|
k 1 |
|
|
|
|
k 1 |
|
|
|
И |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|||||||
соответственно являются главным вектором и главными моментами |
||||||||||||||||||||
системы сил относительно точки О и мгновенной оси относительного |
||||||||||||||||||||
вращения, проходящей через полюс. |
|
|
|
|
|
|
|
|
|
|||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 |
|
|
(8.19) |
|
|
|
|
|
|
|
dA R dr0 |
M d R dr0 |
dt , |
||||||||||||
т. e. элементарная работа системы сил, |
приложенных к свободному твердому |
|||||||||||||||||||
телу в общем случае его движения, складывается из элементарной работы главного вектора системы сил на элементарном поступательном перемещении вместе с какой-либо точкой тела и элементарной работы главного момента этих сил относительно выбранной точки на элементарном вращательном перемещении вокруг этой точки.
211

|
|
|
8.2.5. Работа силы трения |
|
|
||||||||||
Вектор |
|
силы |
трения |
является |
|
|
|
|
|
|
|
|
|||
касательным к траектории движения и |
|
|
|
|
|
|
|
|
|||||||
направлен |
противоположно |
|
вектору |
|
|
|
|
|
|
|
|
||||
скорости точки |
М приложения силы (рис. |
|
|
|
|
|
|
|
|
||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.6). Точка М перемещается по шероховатой |
|
|
|
|
|
|
|
|
|||||||
поверхности по криволинейной траектории. |
|
|
|
|
|
|
|
|
|||||||
ила трен |
я |
определяется |
по |
|
закону |
|
|
|
|
|
|
|
|
||
Кулона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если A F s , |
|
|
|
|
|
|
|
|
|||||||
|
|
FTP |
fN . |
|
|
|
|
|
|
|
|
|
|
|
|
Работа с лы трен я на конечном перемещении М0М1 определяется по |
|||||||||||||||
формуле |
|
|
|
M1 |
|
M1 |
|
|
|
|
|
||||
|
|
|
A – FTPds |
|
|
|
fNds . |
(8.20) |
|||||||
|
|
|
|
M |
0 |
|
|
M0 |
|
|
|
|
|
||
N const, то FTP const и |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
TP |
|
|
|
|
|
|
|
|
|
где s – дл на дуги М0М1, по которой перемещается точка М. |
|||||||||||||||
|
|
|
А |
|
|||||||||||
б8.3. Кинетическая энергия |
|
|
|||||||||||||
|
8.3.1. Кинетическая энергия точки и системы |
||||||||||||||
Кинетической энергией материальной точки называют половину |
|||||||||||||||
произведения массы точки на квадрат ее скорости |
2 |
|
|
|
|||||||||||
|
|
|
T |
mV |
2 |
; |
T |
|
mV |
|
. |
(8.21) |
|||
|
|
|
2 |
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Квадрат модуля скорости равен скалярному квадрату вектора |
|||||||||||||||
скорости, поэтому выражения (8.21) равноценные. |
|
|
|||||||||||||
Кинетическая энергия являетсяДскалярной положительной величиной. |
|||||||||||||||
В СИ единицей кинетической энергии является джоуль: 1 |
ж=1 Н·м. |
||||||||||||||
Кинетической энергией механической системы Т называют сумму |
|||||||||||||||
кинетических энергий всех точек механической системы, т.е. |
|||||||||||||||
|
|
|
|
n m V 2 |
n m V 2 |
|
|
||||||||
|
|
|
T |
|
k k |
|
Иk k |
||||||||
|
|
|
|
|
|
|
|
|
. |
(8.22) |
|||||
|
|
|
|
k 1 |
2 |
k 1 |
|
2 |
|
|
|
||||
Кинетическая энергия как точки, так и системы, не зависит от направления скоростей точек. Кинетическая энергия может быть равна нулю для системы только при условии, если все точки системы находятся в покое.
212
8.3.2. Вычисление кинетической энергии системы. Теорема Кенига
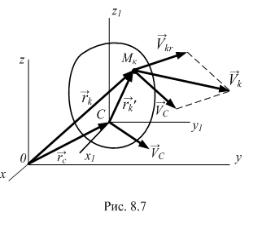
Разложим движение механической системы на переносное поступательное вместе с центром масс системы и относительное по отношению к системе координат, движущейся поступательно вместе с центром масс. Аналогично тому, как это производилось при выводе
формулы для кинетического момента при таком разложении абсолютного |
|||||||||||||||||||||||||||
движения, для каждой точки системы Мк (рис. 8.7) rk |
rc rk . |
|
|||||||||||||||||||||||||
И соответственно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Vk |
|
Vc |
Vkr , |
|
|
|
(8.23) |
|
|
|
|
|
|
|
|
||||||||
времени |
|
|
|
k |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
drk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сгде kr является относительной |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скоростью точки, так как подвижная |
|
|
|
|
|
|
|
|
|||||||||||||||||||
система |
|
коорд нат |
|
движется |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, следовательно, |
|
|
|
|
|
|
|
|
||||||||
поступательно (ω = 0) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
полная про зводная по |
|
|
|
|
от |
r |
|
|
|
|
|
|
|
|
|||||||||||||
совпадает с локальной производной, |
|
|
|
|
|
|
|
|
|||||||||||||||||||
равной относ тельной скорости точки. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
А |
|
|
||||||||||||||||||
Подставляя (8.23) в выражение кинетической энергии абсолютного |
|||||||||||||||||||||||||||
движения системыб, т.е. ее движения относительно системы координат |
|||||||||||||||||||||||||||
Oxyz, из (8.22) после прео разований получаем |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
mk |
Vc |
Vkr Vc Vkr |
|
|
||||||||||
|
|
|
|
T mkVk |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||||||
|
|
|
|
|
|
|
k 1 |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
k 1 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Vc2 |
|
|
|
n |
|
n mkV 2 |
|
n |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
mk |
|
|
|
|
|
|
kr |
Vc |
mkVkr |
. |
|
|
(8.24) |
||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
k |
1 |
|
k 1 |
|
|
|
|
k 1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
n |
|
||||
Преобразуем выражение Vc mkVkr |
Vc mk drk Vc |
d |
mk rk . |
|
|||||||||||||||||||||||
dt |
|
||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
k 1 |
|
dt |
|
k 1 |
|
|||
Поскольку |
|
|
|
|
|
0 |
, |
|
то |
третье |
|
слагаемое |
кинетической |
||||||||||||||
mk r mrkr |
|
|
|||||||||||||||||||||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
энергии Т равно нулю. Учитывая, |
что mk |
m |
– масса системы, и |
||||||||||||||||||||||||
обозначая Tc(r ) |
|
второе слагаемое в (8.24), получим |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mV 2 |
|
|
И |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
c |
Tc(r) , |
|
|
|
|
(8.25) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где Tc(r) |
|
|
k kr |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
213
Величина Tc(r) является кинетической энергией относительного
движения системы относительно системы координат, движущейся |
||||||||
поступательно вместе с ее центром масс, или кинетической энергией |
||||||||
системы относительно центра масс. Формула (8.25) выражает теорему |
||||||||
Кенига: кинетическая энергия системы в абсолютном движении складывается |
||||||||
С |
|
|
|
|
|
|
|
|
из кинетической энергии центра масс, если в нем сосредоточить всю массу |
||||||||
системы, и кинетической энергии системы относительно центра масс. |
|
|||||||
8.3.3. К нетическая энергия твердого тела при |
|
|||||||
|
поступательном движении |
|
|
|||||
ПриT |
|
|
mk |
|
, |
(8.26) |
||
поступательном движении твердого тела скорости всех точек |
||||||||
тела од наковы: Vk |
V , поэтому кинетическая энергия тела равна сумме |
|||||||
кинетическ х энерг |
й всех его точек |
|
|
|
|
|||
|
n m V 2 |
|
V 2 n |
mV 2 |
|
|
||
|
|
k |
k |
|
2 k 1 |
2 |
|
|
|
k 1 2 |
|
|
|
|
|||
где m – масса тела; V – скорость точки тела. |
|
|
|
|||||
|
А |
|
||||||
8.3.4. Кинетическая энергия при вращении тела вокруг |
|
|||||||
бнеподвижной оси |
|
|
|
|||||
При вращении тела вокруг неподвижной оси кинетическую энергию можно вычислить, если учесть, что скорость точки Мk тела можно
выразить по формуле |
|
|
Vk |
hk , |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
где hk – кратчайшее расстояние от точки Мk до оси вращения; ω – угловая |
|||||||||||
скорость тела. |
|
|
|
|
|
|
2 |
|
И |
||
Тогда кинетическая энергия вращающегося тела равна сумме |
|||||||||||
кинетических энергий всех точек телаД: |
|||||||||||
n |
m |
V 2 |
2 |
n |
|
|
|
2 |
|
||
T |
k |
k |
|
|
mk hk2 |
|
J z , |
||||
2 |
2 |
2 |
|||||||||
k 1 |
|
k 1 |
|
2 |
|
|
|||||
или |
|
|
|
T J |
z |
, |
|
(8.27) |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
где Jz – момент инерции тела относительно оси вращения Oz. Следовательно,
вокруг неподвижной оси равна половине произведения момента инерции тела
относительно оси вращения на квадрат угловой скорости тела.
Из сравнения (8.26) и (8.27) следует, что эти формулы математически подобны, отличаются лишь тем, что при вращательном движении
214
аналогом массы является момент инерции тела относительно оси вращения, а аналогом скорости – угловая скорость тела.
Такая аналогия между поступательным и вращательным движениями твердого тела наблюдается во многих формулах, относящихся к этим двум движениям.
8.3.5. Кинетическая энергия тела при плоском движении
При плоском дв жении твердого тела кинетическую энергию можно
вычислять двумя способами: по теореме Кенига или при помощи |
|
мгновенного центра скоростей. Плоское движение тела по теореме Кенига |
|
можно рассматр вать как совокупность двух движений: поступательного |
|
С |
|
переносного дв жен я вместе с центром масс и относительного |
|
имеемmVc2 |
2 |
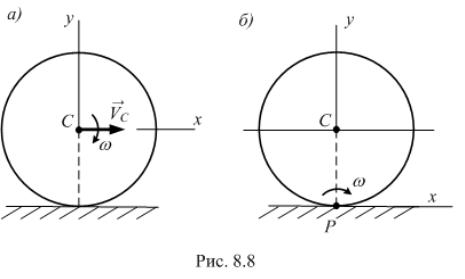
вращательного дв жен я относительно центра масс (рис. 8.8,а)
ледовательно, на основании (8.25) для плоского движения тела |
|||||
б |
|
|
|
||
(р с. 8.8,а) по теореме Кенига |
|
|
|
||
T |
2 |
Jcz |
2 |
. |
(8.28) |
А |
|
||||
|
|
Д |
|
||
Таким образом, при плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей
через центр масс и перпендикулярной плоскости движения (рис. 8.8,а). |
|
|||||
Учитывая, что VC=ω·CP (P – мгновенный центрИскоростей, получаем |
||||||
второй способ определения кинетической энергии твердого тела при |
||||||
плоском движении (рис. 8.8,б): |
|
|
|
|||
T |
2 |
(Jcz m(CP)2 ) J pz |
2 |
, |
(8.29) |
|
2 |
2 |
|||||
|
|
|
|
|||
215

где J pz – момент инерции тела относительно оси Рz, проходящей через
мгновенный центр скоростей перпендикулярно плоскости движения.
Кинетическая энергия тела при плоском движении равна кинетической энергии этого тела при вращении относительно МЦС. Таким образом, плоское
движение, состоящее из двух движений (поступательного и
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вращательного), можно заменять одним вращением вокруг мгновенного |
||||||||||||||||||
центра скоростей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
8.3.6. Теорема об изменении кинетической энергии точки |
|
||||||||||||||||
Для матер альной точки массой m, |
движущейся под действием силы |
|||||||||||||||||
радиуса |
|
|
|
|
|
|
|
|
|
m |
dV |
F |
|
|
||||
F , основной закон д намики можно представить в виде |
|
dt |
. |
|
||||||||||||||
Умножая обе части этого соотношения скалярно на дифференциал |
||||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
||||||||
|
-вектора точки dr , имеем |
|
mdV |
dr |
Fdr |
или |
mVdV Fdr, |
|||||||||||
|
dr |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
где V |
= dt |
– скорость точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уч тывая, что |
dA Fdr |
– элементарная работа, получаем |
|
|
||||||||||||||
|
|
|
А |
|
|
|
|
|
||||||||||
|
|
|
|
mVdV dA . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
mV 2 |
|
|
|
|
|
|
||
Так как |
|
mV 2 |
|
|
|
|
|
|
|
|||||||||
mVdV |
d |
|
|
|
d |
|
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Д |
|
||||||||||||
|
|
|
|
|
mV |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
то окончательно |
|
d |
|
2 |
|
|
|
dA. |
|
|
|
|
|
|
(8.30) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула (8.30) выражает теорему об изменении кинетической энергии для точки в дифференциальной форме: дифференциал кинетической
энергии точки равен элементарной работе силы, действующей на точку. |
||||||||
|
Если обе части выражения (8.30) |
|
|
И |
||||
dA |
N есть мощность, то теорему можно также выразить в виде |
|||||||
dt |
|
|
mV 2 |
|
|
|
|
|
|
|
d |
|
|
|
|||
|
|
|
|
|
|
N . |
|
(8.31) |
|
|
|
|
|
||||
|
|
dt |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Производная от кинетической энергии точки по времени равна мощности, |
|||||||
подводимой к этой точке. |
|
|
|
|
|
|
||
|
Интегрируя обе части (8.30) от точки М0 |
до точки М, получаем |
||||||
теорему об изменении кинетической энергии точки в конечной форме |
||||||||
|
mV 2 |
– |
mV 2 |
A, |
|
(8.32) |
||
|
2 |
2 |
0 |
|
||||
|
|
|
|
|
|
|||
216

т.е. изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.
8.3.7. Сжатие пружины падающим грузом
Тело, имеющее силу тяжести |
P , |
падает без |
С |
с |
высоты h. |
начальной скорости на пружину |
Определить наибольшее сжатие пружины x, если статическое сжат е ее под действием силы тяжести этого тела равно xСТ. Массой пружины можно
пренебречь (р с. 8.9). |
|
|
|
изменен |
|||
Пр |
к дв жению тела теорему об |
||
к |
нет ческой энергии точки |
||
|
mV 2 |
– |
mV 2 |
|
|
0 A . |
|
большем |
|||
|
2 |
|
2 |
Пр мем за начальное положение тела начало его падения с высоты h, |
|||
а за конечное – момент максимального сжатия пружины. Изменение
кинетической энерг |
за этот промежуток времени равно нулю, так как |
|
V0=0 и при на |
сжатии пружины V=0. |
|
|
А |
|
Следовательно, ра ота |
=0, т.к. положительная работа падения тела с |
|
высоты (h+x) равна отрицательной работе сжатия пружины. На тело после его соприкосновения с пружиной действуют две силы: сила тяжести тела
P и сила упругости пружины. Сила P совершает работу на перемещении
(h+x), сила упругости – на перемещении х. |
|
|
|
|
||||||||
|
|
|
|
Д |
||||||||
Следовательно, A |
P(h x) |
c |
x |
2 |
0 . |
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
Р |
|
В положении статического равновесия Р=схCT, а с |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
хСТ |
|
|
h x |
|
1 |
x2 0 или |
|
x2 |
|
И |
||||
Поэтому |
|
|
|
2xСТ x 2xСТ h 0. |
||||||||
|
|
2xСТ |
|
|
|
|
|
|
|
|
||
Решая это квадратное уравнение, имеем |
|
|
|
|
||||||||
|
|
|
x = x + x2 |
|
+ 2x h . |
|
|
|||||
|
|
|
|
СТ |
|
СТ |
|
СТ |
|
|
|
|
Знак плюс перед корнем выбран потому, что х>хCT. При h=0 наибольшее сжатие пружины х=2хCT.
Режим падения груза на упругую систему с нулевой высоты называют
мгновенным приложением постоянной силы к упругой механической системе.
Максимальная динамическая сила в пружине при мгновенном ее нагружении связана со статической силой Р выражением
PДИН K Д Р.
217
Коэффициент K Д в технике называют коэффициентом динамичности,
который равен отношению динамической силы к статической. Согласно выполненному исследованию, при h=0 K Д =2. При ударе двух жестких тел
K Д может принимать значения K Д 100 .
8.3.8. Теорема об изменении кинетической энергии системы
К нет ческую энерг ю Т механической системы можно представить как сумму к нет ческ х энергий всех точек механической системы.
Возьмем про зводную по времени от кинетической энергии стемы
С |
|
|
|
|
|
|
|
|
|
|
|||||
|
n 1 |
|
d |
|
|
n |
dV |
n |
|||||||
dT d |
n m V 2 |
|
2 |
||||||||||||
|
|
|
|
|
|
k k |
|
|
|
|
|
mkVk |
k |
mk akVk |
|
dt |
|
|
|
|
2 |
|
mk |
dt |
Vk |
dt |
|||||
|
|
dt k 1 |
|
k 12 |
|
|
|
k 1 |
k 1 |
||||||
n |
|
|
|
|
|
N e N i . |
|
|
|
|
|
|
|||
F e F i V |
|
|
|
|
|
|
|||||||||
k |
1 |
k |
k |
k |
|
|
|
|
|
|
|
|
|
||
механической |
|
|
|
|
|
|
|||||||||
Итак, |
|
|
|
|
|
|
dT |
N e |
N i . |
|
(8.33) |
||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
Получена теорема |
|
изменении кинетической энергии механической |
|||||||||||||
|
|
|
|
об |
|
|
|||||||||
системы в дифференциальной форме. |
|
|
|
|
|||||||||||
Теорема. Производная по времени от кинетической энергии механической системы равна сумме мощностей внешних и внутренних сил
системы. |
|
|
|
|
|
|
Разделим переменныеАв уравнении и выполним интегрирование левой |
||||||
и правой частей: |
|
|
|
|
|
|
T |
t |
|
t |
N i dt , |
|
|
dT |
|
N edt |
|
|||
To |
0 |
|
0 |
|
|
|
T T |
|
Ae |
Ai |
|
(8.34) |
|
0 |
1 2 |
|
1 2 . |
|
||
|
|
Д |
|
|||
Уравнение (8.34) выражает теорему об изменении кинетической |
||||||
энергии системы в конечной (интегральной) форме. |
|
|||||
|
|
|
|
|
И |
|
Теорема. Изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме работ внешних и
внутренних сил на этом же перемещении.
Если система содержит недеформируемые абсолютно твердые тела, то работа внутренних сил системы равна нулю:
n Aki 0 . k 1
218
9.ПРИНЦИП ДАЛАМБЕРА
9.1.Принцип Даламбера для материальной точки
Законы Ньютона сначала начали применяться для исследования |
|||||||
движения планет Солнечной системы и изучения движения свободных |
|||||||
С |
|
|
|
|
|
||
материальных тел вблизи поверхности Земли. Впоследствии при помощи |
|||||||
основного уравнения динамики Ньютона стали успешно решаться задачи |
|||||||
движен я тел |
определения реакций связей несвободной материальной |
||||||
точки. |
Для зучен я |
движения |
несвободных |
механических |
систем |
||
реакции |
|
|
|
||||
Даламбер предлож л принцип, получивший название принципа |
|||||||
Даламбера, сущность которого в современном понимании заключается не |
|||||||
только в пр влечен |
|
к рассмотрению дополнительных сил, называемых |
|||||
силами |
нерц |
, |
а |
главным образом в применении принципа |
|||
|
освоб |
|
|
||||
освобождаемости от связей к механической системе и получению, |
|||||||
благодаря этому, |
пр нц па расчета, позволяющего определять не только |
||||||
|
внешн х опор, но и реакции связей отдельных частей системы. |
||||||
При помощи акс омы |
ождаемости от связей и аксиомы независимого |
||||||
действ я с л уравнен я движения несвободной материальной точки |
|||||||
являются такими |
же, |
как и для |
свободной |
точки, если к |
силам, |
||
действующим на точку, до авить силы реакции отброшенных связей. Принцип Далам ера в сочетании с принципом освобождаемости от
связей для несво одной материальной точки эквивалентен основному
уравнению динамики Ньютона и , по существу, реализует третий |
закон |
|||
Ньютона. |
Д |
|
||
Основное уравнениеАдинамики материальной точки массой m |
||||
относительно инерциальной системы отсчёта под действием приложенных |
||||
активных сил и реакций связей имеет вид (рис. 9.1) |
|
|
||
|
ma F R , |
|
|
(9.1) |
где m – масса точки; a |
|
И |
||
– ускорение точки; F |
– равнодействующая |
|||
активных сил; R – равнодействующая сил реакций связей. |
|
|||
Назовём вектором силы инерции Ф произведение массы точки на |
||||
вектор ускорения, взятое с обратным знаком: |
|
|
|
|
|
Ф ma . |
|
|
(9.2) |
Если подставить силу инерции в левую часть уравнения (9.1), |
||||
получим основное уравнение динамики в форме Даламбера |
|
|||
|
Ф F R . |
|
|
(9.3) |
Уравнение (9.3) показывает, что сила инерции Ф, действующая на точку,
является силой, противодействующей активным силам и силам реакций.
Форма записи уравнений движения точки М в виде (9.3) соответствует расчетной схеме (рис. 7.2,б), с помощью которой углубляется современное
219
понятие силы инерции несвободной материальной точки: применение принципа освобождаемости от связей к несвободной материальной точке связано с учетом сил реакций связи, а также силы инерции точки, которая
представляет собой силу реакции отсеченного источника гравитационного или других полей на рассматриваемую точку. Сила инерции является
нестационарной силой, т.к. изменяется с течением времени. |
|
||||||
С |
|
|
|
|
|||
|
Как видим, применение принципа Даламбера не связано с |
||||||
дополнительным привлечением к рассмотрению каких-либо фиктивных |
|||||||
сил. |
Пр нц п |
освобождаемости от |
связей |
позволяет превратить |
|||
внутренн е с лы с стемы в реальные действующие внешние силы. При |
|||||||
этом |
с ла нерц |
есть сила реакции, противодействующая |
силам, |
||||
части F R Ф 0 . |
|
(9.4) |
|||||
приложенным к точке, которая характеризует способность массы точки |
|||||||
сопрот вляться |
зменен ю скорости под действием всех сил правой части |
||||||
уравнен я (9.3). |
|
|
|
|
|
||
|
Уравнен ю (9.3) можно придать вид уравнения равновесия без правой |
||||||
|
|
несвободной |
|
|
|||
|
В общем случае форма записи принципа Даламбера (9.4) для |
||||||
материальной точки есть равенство нулю векторной суммы активных сил, сил |
|||||||
|
|
|
|
А |
|
||
реакции и сил инерции |
лю ые моменты времени. Форма записи уравнения |
||||||
движения |
|
|
материальной |
точки, |
по Даламберу, |
в виде |
|
уравнения без правой части напоминает уравнение равновесия статики, но отличается от него тем, что в динамике силы являются переменными
величинами, при этом равенство |
сил соблюдается в любые моменты |
|||
|
|
Д |
||
времени. Для решения векторного уравнения (9.4) выполняют его |
||||
проецирование на оси координат |
|
|
|
|
Fx Rx Фx 0 ; |
Fy Ry Фy 0 ; |
Fz Rz Фz 0 . |
||
Представленные уравнения |
отражают принцип |
аламбера для |
||
|
|
И |
||
несвободной материальной точки в проекциях на оси декартовых координат.
9.2. Многообразие физических свойств силы инерции материальной точки
Выполним сравнение двух форм записи основного уравнения динамики материальной точки в виде основного уравнения динамики Ньютона и в виде принципа Даламбера для несвободной материальной точки. Уравнение (9.1) – основное уравнение динамики точки по Ньютону
– с точки зрения векторной алгебры представляет собой равенство двух векторов левой и правой частей уравнения, равных по модулю и одинаково направленных. Это находится в полном согласии со вторым законом
220
