
Так как векторы VC и VPC лежат на одной прямой (см. рис. 6.8,б) |
и |
направлены противоположно друг другу, |
скорость точки |
Р |
соприкосновения колеса с поверхностью равна нулю: VР=0. |
Вычислим скорость точки А (см. рис. 6.8,б): VA VC VAC , здесь |
|
V AC AC ; |
|
VAC ||VC ; |
VAC |
AC VC . |
С |
|
|
|
|
|
|
|
|
|
|
Тогда |
VA VC VAC |
2VC . |
|
|
|
|
|
|
В данном случае параллелограмм скоростей превратился в систему |
сонаправленных векторов, показанных в точке А на рис. 6.8,б. |
Выч сл м скорость точки М: |
|
VM VC VMC , здесь VMC MC ; |
скорости |
|
|
|
|
|
|
|
|
VMC |
MC R VC . |
Модуль |
|
V |
M |
|
|
V 2 V 2 |
V |
2 . |
|
|
|
|
|
|
|
C |
MC |
C |
Направлен е скорости находим построением параллелограмма |
|
б |
|
|
скоростей (см. р с. 6.8, ). |
Скороcть точки N вычисляем аналогично: |
|
|
V |
N |
V |
2 |
V 2 |
V 2 . |
|
|
|
|
|
C |
NC |
C |
|
Направлен е векторов скоростей VM |
и |
VN находим построением |
|
|
А |
соответствующ х параллелограммов (см. рис. 6.8,б).
6.4. Теорема о проекциях скоростей двух точек тела
Полученная теорема для определения скоростей точек тела с |
помощью формулы (6.2) позволяет получить другие, практически более |
|
Д |
|
удобные и простые методы определения скоростей точек тела. Один из |
таких методов даёт теорема о проекциях скоростей двух точек тела. |
|
Теорема 1. Проекции скоростей двух |
|
|
точек тела на прямую, соединяющую эти точки, |
|
|
всегда равны. |
|
|
|
Рассмотрим две произвольные точки А и |
|
|
В тела (рис. 6.9). Принимая точку А за полюс, |
|
|
получим по формуле (6.2) VB VA VBA . |
|
|
Отсюда, проецируя обе части равенства на линию АВ и учитывая, что |
вектор VBA перпендикулярен к АВ, находим |
И |
|
VB cos VA cos . |
(6.3) |
Теорема доказана. Этот результат позволяет легко находить скорость данной точки тела, если известны направление движения этой точки тела и вектор скорости другой точки того же тела.
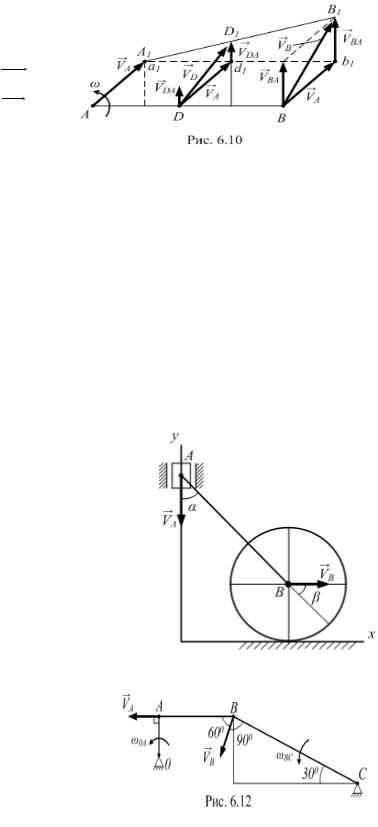
Теорема 2. Концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.
|
Исходя из теоремы о скоростях |
|
|
|
|
|
|
|
|
|
|
точек при плоском движении тела, |
|
|
|
|
|
|
|
|
|
|
|
|
имеем (рис. 6.10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VD |
VA VDA |
VA |
AD ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VB |
VA VBA |
VA AB . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
D1d1 AD |
B1b1 AB |
и, |
следовательно, |
и |
|
|
|
|
|
|
|
|
|
|
|
|
СD1d1 |
|
B1b1 |
или |
|
|
D1d1 |
AD . |
|
|
|
|
|
|
|
|
|
|
|
AD |
|
AB |
|
|
|
|
B b |
AB |
|
|
|
|
|
|
A1d1=AD |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
Т. |
к. |
|
|
A1b1=AB как противоположные стороны |
|
|
|
б |
|
|
|
|
|
|
параллелограммов, то |
D1d1 |
|
A1d1 |
. |
|
Это соотношение показывает, что |
|
|
|
|
|
|
|
|
|
B b |
|
|
A b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
A1D1B1 – отрезок прямой. Из подо ия ∆A1d1D1 |
и ∆A1b1B1 |
|
имеем |
|
|
|
|
|
A1D1 |
|
|
A1d1 |
|
|
или |
|
A1D1 |
|
|
AD |
и |
A1D1 |
AD , |
|
|
|
|
|
A B |
|
А |
|
DB |
|
|
|
|
|
|
|
A b |
|
|
|
|
|
A B |
|
AB |
|
D B |
|
|
|
|
1 |
1 |
|
|
1 1 |
|
|
|
|
|
1 |
1 |
|
|
|
1 |
1 |
|
т. е. расстояния между концами векторов скоростей пропорциональны |
расстояниям между соответствующими точками. |
|
|
|
|
|
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для механизма, изображённого на рис. |
|
|
|
|
|
6.11, найти скорость точки В, если скорость |
|
|
|
|
|
точки А равна VА, угол 450 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
При движении ползуна |
|
в направлении |
VA |
колесо катится вправо и точка В имеет |
скорость VB . Углы α и β образованыД |
векторами |
VA и |
|
VB |
|
с прямой АВ. При |
|
|
|
|
|
α=β=450 по формуле (6.3) VAcos450=VBcos450, |
|
|
|
Рис. 6.11 |
откуда VB=VA. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. Кривошип ОА (рис. 6.12) |
|
|
|
|
|
|
|
|
длиной 1 м вращается с угловой |
|
|
|
|
|
|
|
|
скоростью |
|
ОA 2 рад/с. |
Определить |
|
|
|
|
|
|
|
|
скорость точки В. |
|
При |
|
заданном |
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
направлении |
вращения кривошипа |
ОА |
|
|
|
|
|
|
|
|
его скорость будет определяться
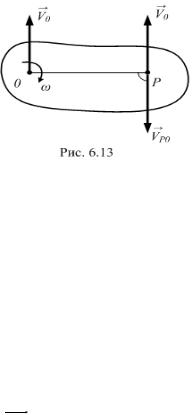
вектором VA . Величина скорости |
VA OAOA 2 1 2 |
м/с . |
|
|
Кривошип ВС при этом будет вращаться вокруг точки С с угловой |
скоростью ωВС, и скорость точки В определится вектором VB . По формуле |
(6.3) V |
A |
V |
B |
cos 600 , откуда VB = |
VA |
|
= |
2 |
= 4 м/с . |
|
|
cos600 |
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
6.5. Определение скоростей точек тела при помощи |
|
|
|
|
|
|
|
мгновенного центра скоростей |
|
|
|
|
|
|
|
|
|
6.5.1. Мгновенный центр скоростей |
|
|
|
Другой простой |
наглядный метод определения скоростей точек тела |
Сплоском дв жен |
основан на понятии мгновенного центра скоростей. |
Кроме того, |
это понят е позволяет определять угловую скорость тела при |
плоском дв жен . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
Теорема. В каждый момент времени при плоском движении тела, если |
0 , |
|
|
меется ед нственная точка в |
плоскости его движения, скорость |
которойприравна нулю. Эту точку называют мгновенным центром скоростей |
(МЦС). Обознач м её |
уквой Р. Для доказательства теоремы обратимся к |
теореме о сложен |
скоростей (6.2). |
|
|
|
|
|
|
|
|
На рис. 6.13 точка О имеет скорость VO , а |
|
|
|
|
тело – угловую скорость ω заданного |
|
|
|
|
направления. Тре уется найти такую точку Р, |
|
|
|
|
скорость которой равна нулю. Для этого запишем |
|
|
|
|
теорему, |
|
удовлетворяя |
|
Д |
|
|
заданное |
|
условие |
|
|
|
|
VP VO VPO 0 . |
|
А |
|
|
|
Равенство нулю этого выражения возможно в том случае, если |
векторы Vo |
|
и VPO |
будут в точке Р равны по модулю и противоположны |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
друг другу по направлению: VO VPO . |
|
Если VO |
VPO |
; VPO OP , |
то |
OP VO |
.Таким образом, |
точка |
Р – МЦС на |
рис. |
6.13 |
находится |
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикуляре к вектору VO справа на расстоянии OP. |
менно в этой |
точке векторы VO |
и VPO равны друг другу по модулю и противоположны |
по направлению, поэтому скорость точки Р равна нулю.
Если положение МЦС известно, то, приняв его за полюс Р, можно
определить скорость, например, точки А следующим образом (рис. 6.14): |
VA VAP ; |
VA AP ; |
VA AP, |
здесь АР – радиус, на котором вращается точка А относительно МЦС. Скорость точки В вычислим аналогично:
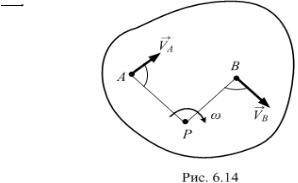
VB VBP ; |
VB BP ; |
VB BP . |
и VB |
Из полученных выражений для VA |
имеем |
|
VA |
|
|
VB |
|
или |
|
AP |
BP |
|
|
|
|
|
|
МЦС |
|
VA AP . |
(6.4) |
|
VB |
BP |
|
|
|
|
|
|
|
|
|
ледовательно, если положение МЦС известно, то скорости точек
тела выч сляют так же, как и в случае вращения тела в плоскости вокруг |
расстояниям |
ω. При этом скорости точек тела |
с угловой скоростью |
пропорц ональны |
от точек до МЦС. Таким образом, задача |
расчёта скоростей точек плоской фигуры упрощается, если известно
положен е мгновенного центра скоростей тела в любой момент времени. |
|
общих |
|
6.5.2. Спосо ы нахождения мгновенного центра скоростей |
В некоторых случаях из условия движения удаётся сразу указать |
точку плоской |
ф гуры, скорость которой в рассматриваемый момент |
|
|
|
|
|
А |
времени равна нулю. Эти точки и являются мгновенными центрами |
скоростей. |
В |
других |
наи олее |
|
случаях положения МЦС |
определяют, рассматривая параметры движения тела и скорости двух |
точек тела. |
|
|
|
|
|
|
|
|
|
и направление скорости точки В. |
Случай 1. Известна скорость точки |
МЦС находится на пересечении перпендикуляров к скоростям, |
проведённых в точках |
|
и В (рис. 6.15). |
|
|
В этом случае |
|
|
|
|
VA |
; |
VB BP . |
|
|
|
|
|
|
|
|
|
|
|
|
|
AP |
|
|
|
Случай 2. Известна скорость точки А тела и угловая скорость ω. МЦС |
находится на перпендикуляре к вектору VА в точке А на расстоянии АР |
(рис. 6.16): |
АР |
VA |
. |
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случай 3. Известны длина отрезка АВ, скорости VA и VВ двух точек |
тела, которые перпендикулярны к отрезку АВ и направлены в одну сторону |
(рис. 6.17). |
И |
|
МЦС находится на продолжении отрезка АВ в точке пересечения с прямой, проведенной через концы векторов VA и VB . Для определения ω
составляем выражение |
VA |
|
VB , откуда |
BP |
VB |
AB . |
|
АВ |
ВР |
BP |
|
VA VB |
|
Случай 4. Известны длина отрезка АВ, скорости VA и VB двух точек |
тела, которые перпендикулярны |
отрезку АВ и |
направлены |
в разные |
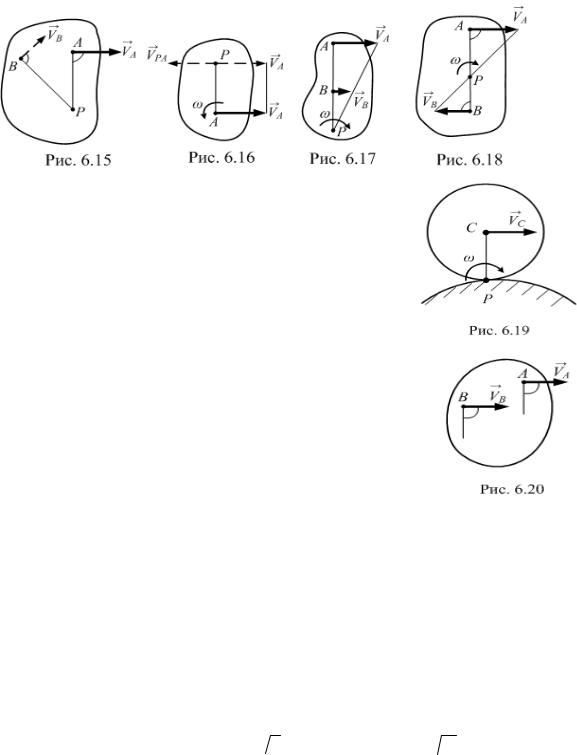
стороны (рис. 6.18). МЦС находится внутри отрезка АВ. Для определения
ω составляем выражение |
|
VA |
|
VB |
, откуда АР |
V |
А |
AB. |
AP |
AB AP |
|
|
|
|
|
VA VB |
С |
лучай 5. На р с. 6.19 тело перекатывается без |
проскальзыван я по поверхности неподвижного |
тела. МЦС наход тся в точке соприкосновения тел в |
точке Р. |
|
и |
Случай 6. На рис. 6.20 скорости двух точек тела |
|
б |
параллельны. В этом случае МЦС находится в |
бесконечности, т.е. отсутствует. Тело совершает |
мгновенное поступательное движение, тогда скорости |
двух точек и всех других точек тела одинаковы, а их |
ускорения в общем случае могут быть разными. |
|
А |
неподвижной плоскости, имея скоростьДцентра V0 . Определить скорости точек А, М, N обода колеса в данный момент времени.
Пример 4.
Колесо радиусом R (рис. 6.21) катится без скольжения по
Решение.
Мгновенный центр скоростей в этом случае находится в точке Р
|
соприкосновения |
колеса с |
плоскостью. |
Угловая |
скорость |
колеса |
|
определяется по |
формуле |
|
V0 |
|
V0 |
. |
Скорости |
указанных |
точек |
|
ОP |
R |
|
|
|
|
|
|
|
И |
|
определим с помощью МЦС: |
VA AP 2V0 ; |
|
|
|
VM VN MP V0  2 , т.к. МР NP R
2 , т.к. МР NP R 2.
2.
Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками в направлении вращения.
ДИНАМИКА
7. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 7.1. Исходные положения
В разделе «Динамика» изучают механические движения материальных объектов под действием сил. Простейшим материальным объектом природы является материальная точка. Более сложные материальные объекты – механические системы и сплошные тела –
Сла является в механике основным, первичным понятием. Свойства сил, пр ложенных к твердому телу или точке при отсутствии движения,
считают состоящ ми з материальных частиц. Каждую такую частицу считают матер альной точкой.
по нтенс вности статического давления.
В качестве эталона силы обычно принимают линейную силу упругости, т. е. такую с лу, модуль которой при действии, например, на пружину д намометра пропорционален деформации пружины.
В разделе «Д нам ка» силы оценивают по их динамическому |
оценивают |
действ ю. |
|
Если одну ту же силу приложить к разным телам, свободным от |
других воздействий, то за один и тот же промежуток времени эти тела |
пройдут разные расстояния и удут иметь разные скорости. Это явление |
|
б |
объясняется различной инертностью тел. |
Инертностью называется свойство материальных тел сопротивляться |
изменению скорости движенияАпод действием приложенных сил. Количественной мерой инертностиДтела является его масса m. Это
скалярная физическая величина, постоянная для данного тела. В общем случае инерционные свойства тела определяются не только его массой, но и формой тела, а также зависят от распределения масс в объеме тела. Чтобы отвлечься от влияния этих факторов, на первом этапе изучения динамики вводят понятие «материальная точка»И.
Материальной точкой называют материальное тело, совершающее движение, размерами которого можно пренебречь.
Возможности замены материального тела материальной точкой зависят от условий конкретной задачи и будут рассмотрены в дальнейшем.
Движение материальных объектов рассматривается в системах отсчета и совершается в пространстве с течением времени. В классической механике, в основу которой положены законы Ньютона, пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от скорости движущихся в нем материальных объектов. Положение точки в таком пространстве относительно какой-либо системы отсчета определяют тремя независимыми параметрами или координатами точки. Время в классической механике универсально. Оно не связано с
196
пространством и скоростью материальных объектов. Во всех системах отсчета, движущихся друг относительно друга, оно протекает одинаково. В классической механике время определяется по какому-либо периодическому процессу, например периоду вращения Земли вокруг своей оси, колебаниям маятника. Классическая механика Ньютона не
накладывает ограничения на величину максимальной скорости движения материальных объектов.
|
|
|
|
|
7.2. Законы динамики |
|
В основе д нам ки лежат физические законы, установленные |
опытным |
путем |
|
проверенные многовековой |
практикой |
человечества. |
С |
|
ыли впервые изложены И. Ньютоном в его |
истемат чески эти законы |
классическом |
|
соч нен |
«Математические |
начала |
натуральной |
философ |
», |
зданном 1687 г. |
|
|
Первый закон (закон инерции), открытый Галилеем (1638 г.), гласит: |
|
|
от внешн х воздействий материальная точка сохраняет свое |
изолированнаясостоян е покоя равномерного прямолинейного движения до тех пор, пока |
|
б |
|
|
приложенные с лы не заставят изменить состояние точки. Движение,
совершаемое точкой при отсутствии сил, называют движением по инерции.
Закон инерции отражает одно из основных свойств материи:
пребывать неизменно в движении и устанавливает для материальных тел |
эквивалентность состояния покоя и движения по инерции. Из него следует, |
что если F 0 |
, то точка покоится или движется с постоянной по модулю и |
|
Д |
направлению скоростью (V const ); ускорение точки при этом равно нулю |
( a 0 ); если |
же движениеАточки не является равномерным и |
прямолинейным, то на точку действует сила. |
Систему отсчета, по отношению к которой выполняется закон инерции, называют инерциальной системой отсчета. Солнце с планетами
является изолированной механической системой,Ина которую не действуют
силы со стороны других галактик, поэтому центр масс такой системы перемещается прямолинейно или находится в покое. Система отсчета, начало которой находится в центре Солнца, две оси расположены в плоскости орбиты Земли, является прямоугольной гелиоцентрической инерциальной системой
отсчета.
При решении большинства задач динамики инерциальной системой, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.
Второй закон (основной закон динамики) устанавливает изменение скорости точки при действии на нее силы.
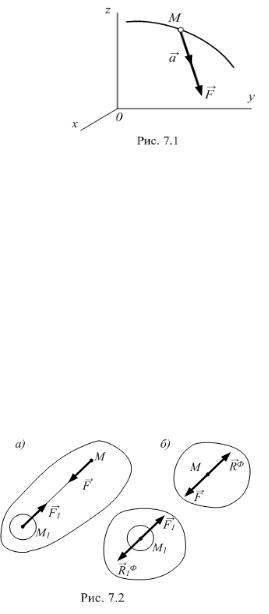
Он гласит: произведение массы точки на ускорение, которое она получает под действием силы, равно по модулю этой силе, а
направление |
ускорения |
совпадает |
с |
направлением силы (рис. 7.1). |
|
|
Математически этот |
закон выражают |
С |
|
|
|
векторным равенством |
ma F . |
|
|
|
(7.1) |
Трет й закон Ньютона (о равенстве сил действия и противодействия) |
определяет свойство с л взаимодействия между двумя материальными точками: с лы вза модействия двух материальных точек направлены по линии,
появитьсятолько как результат взаимодействия двух тел. Второе тело на данном р сунке отсутствует, поэтому рассмотрим изолированную
соединяющей эти точки, равны по величине и противоположны по направлен ю. Используем законы Ньютона для обоснования расчетной
схемы (см. р с. 7.1) уяснения физической сущности основного закона динамики (7.1).
Согласно определен ю понятия «сила», на рис. 7.1 сила F может
механическую с стему, состоящую из двух тел: M1 – Земля; М – тело, |
свободно падающее на поверхность Земли (рис.7.2,а). |
Гравитационноебвзаимодействие |
двух тел, по третьему закону Ньютона, |
записывается векторным уравнением |
F1(t) F (t) . |
(7.2) |
Сравнивая уравнения (7.1) и (7.2), |
А |
видим, что их правые части совпадают. |
Теперь применим к механическойДгравитационной системе двух тел (см. рис. 7.2,а) принцип освобождаемости Иот связей. Отсечем от механической гравитационной системы свободно падающее тело М. Отбросим нижнюю часть системы и рассмотрим равновесие оставшейся
верхней части. Согласно принципу освобождаемости от связей, для идеальной гравитационной связи необходимо к телу М приложить силу реакции со стороны отброшенной части механической системы, которой в
данном случае является сила RФ , равная по модулю и противоположная
по направлению гравитационной силе F .
Уравнение движения тела М можно записать в виде векторного
уравнения взаимодействия сил |
|
RФ F(t) . |
(7.3) |
Представленные уравнения (7.1), (7.2), (7.3) имеют общую правую
часть, которая в частном случае свободного падения тела у поверхности
Земли представляет собой силу гравитационного притяжения F(t) тела М
к центру Земли. При этом левые части этих уравнений являются различными. В основном уравнении динамики точки (7.1) левая часть представлена в виде произведения массы тела на ускорение, причем направление вектора ускорения совпадает с вектором действующей силы.
В уравнении (7.2) левая часть представляет собой математическую неопределенность – произведение бесконечно большой массы Земли (по
сравнению с массой падающего тела М) на бесконечно малое ускорение |
Земли, обусловленное с лой F гравитационного притяжения со стороны |
тела М. Неопределенность типа 0 по третьему закону Ньютона можно |
заменить экв валентным произведением массы тела М на его ускорение. |
С |
|
И, наконец, в уравнен (7.3) левая часть – это сила реакции отброшенной |
части грав тац онного поля Земли на рассматриваемое тело М. |
Дальнейшее |
е уравнений (7.2), (7.3) продолжим в подразделе |
«Принц п Далам ера |
для несво одной материальной точки». Сейчас |
обратимсяк основному уравнению динамики точки (7.1), которому
полностью совпадаетобсужденс ньютоновской расчетной схемой (см. рис.7.1), т.к. малую силу F1, приложенную к ольшой массе тела M1 , рассматривать не
соответствуют расчетные схемы рис.7.1 и 7.2, а. На расчетной схеме (см.
рис. 7.2,а) тело М пр тягивается к неподвижному телу M1 , с которым
связана неподвижная система координат. Такая расчетная схема
следует. Ньютону не ыл известен принцип освобождаемости от связей в
современном представлении, |
поэтому он представил левую часть |
А |
|
Д |
уравнения (7.1) в виде произведения массы тела на ускорение.
Это позволило Ньютону создать дифференциальное и интегральное исчисления. В результате, используя расчетную схему (см. рис. 7.1), стало возможно ввести время t в уравнение (7.1) и выполнить интегрирование
дифференциальных уравнений |
с целью получения первых и вторых |
|
|
|
И |
интегралов, т.е. определить скорость движения и уравнение движения |
точки как функции времени. |
|
|
|
|
Второй закон динамики, как и первый, имеет место только по |
отношению к |
инерциальной |
системе |
отсчета. |
з этого |
закона |
непосредственно видно, что мерой инертности материальной точки |
является ее масса. Если на точку действует одновременно несколько сил, |
то они будут эквивалентны одной равнодействующей силе R, |
равной |
геометрической сумме этих |
|
|
|
|
сил. |
|
|
|
|
|
Тогда равенство (7.1) принимает вид |
|
|
|
|
ma R |
или |
ma Fi . |
(7.4) |
В отличие |
от инертной |
массы |
массу m, |
входящую |
в закон |
всемирного тяготения Ньютона (1.1), называют гравитационной массой. С большой степенью точности экспериментально установлена эквивалентность инертной и гравитационной масс. Массу обычно
определяют по силе тяготения |
F и ускорению свободного падения g у |
поверхности Земли. |
|
|
|
огласно (7.1), в этом случае имеем |
|
|
|
m = F . |
(7.5) |
|
|
g |
|
Это определен е массы широко используют в механике Ньютона. |
|
Четвертый закон |
Ньютона |
(аксиома) независимого действия |
сил |
(принц п суперпоз ц |
), по существу, является законом параллелограмма |
С, при помощи которого действующие на точку силы заменяются одной |
равнодействующей с лой. |
|
|
силдействия друг х с л.
Закон незав с мого действия сил утверждает, что каждая сила,
действующая на точку, создает соответствующее ускорение независимо от
Для измерениябмеханических и физических величин достаточно ввести три основные единицы измерения: длину, время, массу.
7.3. Системы единиц
В международной системе единиц СИ (SI от Le systeme international d’ unites) основными единицами измерения являются метр (м), секунда (с) и
килограмм массы (кг). Единицей измерения силы является производная |
единица ньютон (Н) – это сила, сообщающая телу массой в 1 кг ускорение |
в 1 м/с2. |
А |
В стационарном гравитационномДполе Земли для тел, находящихся в покое, сила притяжения 1 кг массы тела к центру Земли равна произведению 1 кг массы тела на вес g единицы массы
g=9,81 м/c2 = 9,81 Н/кгИ.
7.4. Дифференциальные уравнения движения материальной точки
Используя аксиому о связях и силах реакций связей, можно получить дифференциальные уравнения движения несвободной точки так же, как и для свободной, если ко всем приложенным к точке силам добавить силы реакций связей. Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой









