
2164
.pdf
4. ПЛОСКИЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ ДЛЯ ПЕРЕДАЧИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Современные двигатели, как правило, быстроходные, с небольшим диапазоном изменения скоростей, поэтому зачастую режим работы вала двигателя не совпадает с режимом работы машины орудия. В силу этого передача движения от вала двигателя к машине производится посредством различных передач точных механизмов.
4.1.Основные виды зубчатых передач
Взависимости от конструктивного оформления механизмы подразделяются на ряд основных групп: рычажные, кулачковые, зубчатые, клиновые, винтовые, фрикционные, механизмы с гибкими связями, механизмы с упругими звеньями и др. Не рассматривая всего этого большого разнообразия механизмов, более подробно остановимся на зубчатых передачах, широко применяемых в колесных и гусеничных машинах.
Взависимости от области применения передачи условно делят на кинематические и силовые. Кинематические передачи используют в приборах, следящих системах и других устройствах, где передаются небольшие мощности, но требуется высокая кинематическая точность. Примером являются механизмы наведения и стабилизации вооружения, танковая навигационная аппаратура и др. Силовые передачи широко применяются во всех случаях, когда требуется передать значительные мощности, в частности, в трансмиссиях боевых и транспортных машин. К силовым передачам этих машин предъявляют следующие требования: стабильность передачи крутящего момента, малые механические потери, высокая надёжность, малые нагрузки на вращающие валы, малые габариты и вес. В наибольшей степени таким требованиям удовлетворяют зубчатые передачи. Из всех видов зубчатых передач наиболее распространены плоские передачи с цилиндрическими прямозубыми колёсами (75 % от всех зубчатых передач). Примером служит планетарная коробка передач, коробка скоростей, входной редуктор танка, бортовая передача и т.д.
Взубчатых цилиндрических передачах вращение передается
силами давления, возникающими на поверхности зубьев, находящихся в зацеплении.
Цилиндрические зубчатые передачи в зависимости от расположения зубьев по отношению к образующей цилиндра зубчатого колеса подразделяются на прямозубые, косозубые и шевронные (рис. 4.1).
Рис. 4.1. Прямозубая цилиндрическая |
Рис. 4.2. Зубчатые колеса при |

Цилиндрические зубчатые механизмы по кинематическому признаку делятся на две большие группы:
–зубчатые механизмы с неподвижными осями всех зубчатых колёс, называемые рядовыми, ступенчатыми и простыми передачами;
–зубчатые механизмы с подвижными осями некоторых колёс, называемые эпициклическими,
или планетарными, передачами.
Основой простых передач служит ступень, состоящая из двух сопряжённых зубчатых колёс. Ступенью принято называть передачу, в которой может самостоятельно осуществляться преобразование угловой скорости и крутящего момента. При этом зубья ведомого колеса передачи могут располагаться на внешней или внутренней поверхности цилиндра (рис. 4.1, 4.2). При внутреннем зацеплении характерно вращение обоих колес в одну сторону. Если же зубья расположены на внешних поверхностях цилиндра, передача называется цилиндрической с внешним зацеплением. В одной простой передаче достигается сравнительно малое изменение угловой скорости и расстояние между валами получается небольшим.
По числу ступеней передачи подразделяются на одноступенчатые и многоступенчатые.
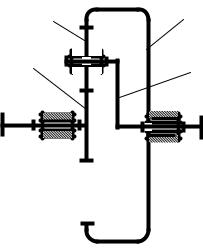
Если требуется значительное изменение угловой скорости, то применяются многоступенчатые передачи, в которых выходной вал предыдущей ступени служит входным валом последующей ступени (рис. 4.3).
Если требуется при небольшом изменении величины угловой
ω1 |
z1 |
|
|
|
1 |
z3 |
|
|
z2 |
||
ω2 |
2 |
|
|
|
z4 |
||
ω3 |
3 |
||
|
|||
|
z5 |
|
|
|
4 |
|
|
ω4 |
|
z6 |
ω1 |
z1 |
|
|
1 |
|
|
z2 |
|
ω2 |
2 |
|
z3 |
||
ω3 |
||
3 |
||
|
z4 |
|
|
4 |
|
ω4 |
|
Рис. 4.3. Многоступенчатая передача |
Рис. 4.4. Передача с “паразитными” |
|
колесами |
скорости передать движение между валами, находящимися на значительном расстоянии друг от друга, или изменить направление вращения, то применяются "паразитные" рядовые
101
передачи (рис. 4.4). Примером рядовой передачи может |
|
|||||||||
служить входной редуктор танка. |
|
|
|
|
|
|||||
Зубчатые передачи, оси отдельных колес которых подвижны, делятся |
||||||||||
на планетарные и дифференциальные. Такие зубчатые механизмы с |
||||||||||
одной степенью свободы называются планетарными, а с двумя и более |
||||||||||
степенями свободы – дифференциальными. В этих механизмах колеса |
||||||||||
с подвижными осями называются сателлитами, а звено, на котором |
||||||||||
располагаются |
оси |
сателлитов,– |
водилом. |
Зубчатые |
колеса с |
|||||
b1 |
|
1´ |
неподвижными |
осями |
|
вращения |
||||
|
называются |
|
солнечными, |
или |
||||||
|
|
|
|
|||||||
1 |
|
01 |
центральными, неподвижное колесо – |
|||||||
|
опорным. Планетарные передачи (рис. |
|||||||||
|
|
|
4.5), при условии правильного выбора |
|||||||
|
|
|
их конструкций и параметров, имеют |
|||||||
|
|
|
меньшие габариты, более высокий |
|||||||
|
|
|
КПД и меньшую массу, чем простые |
|||||||
|
|
|
передачи. Это обусловило широкое |
|||||||
|
|
|
применение |
планетарных |
|
передач в |
||||
|
|
|
бронетанковой |
технике |
|
и |
других |
|||
|
|
|
колесных |
и |
гусеничных |
машинах, а |
||||
Рис. 7.5. |
|
именно: |
планетарные |
|
механизмы |
|||||
Рис. 4.5. Схема планетарного |
|
|||||||||
механизма Джемса |
поворотов, |
многорядные |
бортовые |
|||||||
редукторы и т.д. |
|
|
коробки |
передач, дифференциальные |
||||||
|
|
|
|
|
|
|
|
|
|
|
4.2. Передаточное отношение и передаточное число
Основными характеристиками зубчатых передач являются передаточные отношения и передаточное число.
Передаточным отношением называется отношение угловой скорости ведущего звена к угловой скорости ведомого звена и обозначается буквой i с соответствующими индексами. Таким образом,
величины |
i |
|
1 |
и |
i |
|
2 |
представляют собой передаточные отношения одной и той же |
|
|
|
|
|||||||
12 |
|
2 |
21 |
|
|||||
|
|
|
|
|
|
1 |
|
||
зубчатой передачи при различных ведущих колесах.
При равномерном вращении обоих колес передаточное отношение можно выразить через число оборотов в минуту:
i |
|
1 |
|
n1 |
|
|
2 |
n2 . |
|||||
12 |
|
|
||||
102

Если ведомое и ведущее колеса вращаются в одну сторону (например, у зубчатой передачи с внутренним зацеплением), то передаточное отношение считается положительным. Если ведомое и ведущее колеса вращаются в разные стороны (например, у зубчатой передачи внешнего зацепления, то передаточное отношение считается отрицательным.
Кроме передаточного отношения, существует еще понятие передаточного числа. Передаточным числом называют отношение числа зубьев большего колеса, как правило, ведомого к числу зубьев меньшего – ведущего. Таким образом,
u = z2 / z1,
|
|
|
|
Рис. 10.2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.6. Цилиндрическая |
Рис. 4.7. Цилиндрическая |
||||
Рис. 4.8. Ступенчатая |
|
|
|
||
|
Рис. 10.1 |
передача внутреннего зацепления |
|||
передача внешнего зацепления |
|||||
|
передача |
|
|
|
|
где z1, z2 – число зубьев колес 1 и 2 (см. рис. 4.1).
Необходимость применения сложных передач возникает чаще всего, когда передаточное число выходит за пределы, допускаемые для одной пары зубчатых колёс.
Передаточное число тем больше, чем больше число зубьев z2 колеса и чем меньше число зубьев z1 шестерни. Минимальный предел, который определяется из условия неподрезания ножек, z1=14...17. Что касается z2, то теоретически верхнего предела нет, но практически это 120...150. Однако в конструкторской практике для цилиндрических передач передаточное число принимается u=5...7, так как с его ростом увеличиваются габариты передачи и её вес, а также возникают трудности изготовления. Поэтому, когда передаточное число больше установленного предела, прибегают к многоступенчатой передаче.
Рассмотрим методы определения передаточных чисел сложных механизмов через заданные числа зубьев, предварительно условившись о правилах определения знака передаточного числа.
Взубчатой передаче (рис. 4.6) с внешним зацеплением зубчатые колеса вращаются в противоположных направлениях, следовательно, передаточное число должно быть принято отрицательным .
Впередаче с внутренним зацеплением (рис. 4.7) зубчатые колеса вращаются в одну сторону, поэтому передаточное число положительно. Рассмотрим соединение зубчатых колес, в которых имеется k параллельных валов, т.е. ступенчатую передачу. Выписываем для каждой из пар зубчатых колес передаточное число, не учитывая пока его знака:
u |
z2 |
|
n1 |
; u |
|
|
z3 |
|
n2 |
|
|
z |
n |
|
|
n , … |
|||||||
12 |
|
|
23 |
|
z |
2 |
|
||||
|
1 |
2 |
|
|
|
|
3 |
|
|||
u u |
23 |
u |
k 1,k |
|
n1 |
|
|
z2 z3...zk |
. |
|
|
|
|||||||
12 |
|
|
nk |
|
|
|
|||
|
|
|
|
|
|
|
z1z2 zk 1 |
||
Перемножив почленно выражения передаточных чисел простых передач, входящих в состав |
|||||||||
ступенчатой, получим полное передаточное |
число |
ступенчатого механизма, равное произведению |
|||||||
103

передаточных чисел простых ступеней, входящих в состав данной ступенчатой. Полному передаточному числу можно присвоить определенный знак.
u 1 n1 z2 1 z2 .
2 n2 z1 |
z1 |
Если в ступенчатом зацеплении m внешних зацеплений, то при переходе от одного вала передачи к другому происходит m раз изменение знака угловой скорости. Таким образом, об окончательном знаке угловой скорости можно судить по числу внешних зацеплений. Вследствие этого полное передаточное число со знаком нужно выразить так:
u |
|
n1 |
|
z2z3...zk |
1 m. |
||
|
|
||||||
1k |
|
nk |
|
z1z |
|
|
|
|
|
|
2 |
...zk 1 |
|||
Учитывая, что в рядовой передаче на каждом из валов закреплено по одному колесу, входящему одновременно в зацепление с колесами на предыдущем и последующем валах, полное передаточное число рядовой передачи можно получить, приняв z2 = z΄2, z3 = z΄3, z4 = z΄4 и т.д.
u1k n1 zk 1 m. n2 zk 1
Последнее выражение показывает, что «паразитные колеса» в рядовых передачах на величину передаточного числа не влияют, однако их включение может изменить знак передаточного числа.
При совпадении направлений осей первого и последнего колес ступенчатого зацепления ряд называется возвратным, а передача – соосной (рис. 4.10). Соосная передача нашла широкое применение в редукторах, коробках скоростей, эпициклических передачах и других механизмах.
Рис. 4.9. Рядовая передача
Редуктором принято называть механизм, составленный из зубчатых колес, предназначенных для уменьшения числа оборотов ведомого вала по сравнению с числом оборотов
ведущего вала (|u| > 1). Если при помощи механизма число оборотов ведомого вала увеличивается, то его называют мультипликатором (|u| < 1).
Приведенные примеры показывают, что передаточное отношение многоступенчатой передачи
Рис. 4.10. Соосная передача
Рис. 10.5
равно дроби, числитель которой представляет произведение всех чисел зубьев ведомых колес, а знаменатель – произведение всех чисел зубьев ведущих колес.
В общем случае, когда учитываются погрешности изготовления зубьев зубчатых колес, то i12 = ω1 /ω2 – величина переменная. При этом приравнивать передаточные числа и передаточные отношения нельзя.
104

4.3. Цилиндрическая эвольвентная зубчатая передача
4.3.1. Эвольвентный профиль зуба
Условие, которому должны удовлетворять сопряжённые профили зубьев, заключается в том, что общая их нормаль в точке касания должна проходить через полюс зацепления. Этому условию удовлетворяют различные кривые, но наибольшее применение получила эвольвента (рис. 4.11).
Если по неподвижному кругу b будем перекатывать прямую nn без скольжения, то любая точка этой прямой М и прочертит эвольвенту в плоскости. Окружность, по которой катится прямая, называется основной b окружностью, а прямая n-n – производящей прямой. Производящая прямая
Рис. 4.11. Построение эвольвенты как траектории движения точки
является нормалью эвольвенты в любой точке. На основной окружности лежат центры кривизны эвольвенты. Две эвольвенты,полученные с помощью одной основной окружности, будут эквидистантными кривыми или равноотстоящими. Координаты точки М на эвольвенте определятся как
105

Рис. 4.12. К доказательству теоремы зацепления
ОМ = rв / соsα,
где угол α связан эвольвентной функцией (инволютой) соотношением = inv α = tg α – α –уравнение эвольвенты.
4.3.2. Основная теорема зацепления
Выясним, какому основному условию должны удовлетворять профили зацепляющихся зубьев, чтобы от момента входа в зацепление и до выхода из него обеспечивалось постоянство передаточного отношения 1/ 2 (без учета погрешностей изготовления зубьев зубчатых колес).
Рассмотрим соединение профилей зубьев в точке С (рис.4 .12). Пусть ведущее колесо вращается около неподвижной оси 01 с постоянной угловой скоростью 1, а второе ведомое колесо – с постоянной угловой скоростью 2 относительно оси вращения 02. При этом
1= 1R1 , 2= 2R2.
Проведем в точке С общую нормаль n – n и общую касательную t – t, после чего разложим скорости на составляющие c1 и c2 , направленные по нормали и по касательной. Рассмотрим составляющие c1 и c2 и выясним вопрос о возможности существования неравенств c1> c2 или c1< c2. Если эти составляющие скоростей не равны, то зуб шестерни должен врезаться в зуб колеса или наоборот и нарушится контакт. Отсюда вытекает c1= c2. Опустим из центров колес на нормаль n – n перпендикуляры О1К1 и О2К2, из подобия треугольников C01K1 и A1CC1, а также C02K2 и A2C2C.
CC1 / 01K1 = A1C/C01 или c1 / ro1 = 1/R1; => c1 = 1·(ro1/R1).
CC2 / 02K2 = A2C/02C или c2 / ro2 = 2 / R2,
откуда
c2 = 2(ro2 / R2) = 2ro2.
Так как c1 = c2, получаем 1ro1 = 2ro2 или 1 / 2 = ro2 / ro1 = const; u = | 1 / 2| = r2 / r1 = d2 / d1 = const,
106

где u – передаточное число.
Полученный результат показывает, что нормаль, проведённая в любой точке касания профилей зубьев, делит в точке W линию центров 0102 на отрезки, отношение которых обратно пропорционально отношению угловых скоростей звеньев передачи.
Вывод: для обеспечения постоянства передаточного числа в любой момент работы передачи необходимо так спрофилировать рабочие участки зубьев, чтобы общая нормаль к ним в любой точке касания проходила через постоянную точку (полюс зацепления), лежащую на линии центров и делящую её в отношении, обратно пропорциональном отношению угловых скоростей. Основное требование: сохранение постоянства передаточного числа.
4.3.3. Основные размеры зубчатых колес
Эвольвентные профили зубьев, как было показано, удовлетворяют основному условию синтеза зубчатого зацепления – получению заданного передаточного числа. Выполнение дополнительных условий синтеза зависит в первую очередь от размеров колеса. Эти размеры удобно задавать в долях какойлибо одной линейной величины, связанной с зубом. Чтобы пояснить выбор этой величины, выразим длину некоторой окружности, имеющей диаметр d, через число зубьев колеса z:
d = pz,
где p – окружной шаг, т.е. расстояние, измеренное по дуге окружности диаметром d между двумя соответствующими точками соседних звеньев.
Отсюда
d = (р / )z = mz,
где m – отношение окружного шага к числу , называемое модулем зуба.
Окружной шаг и модуль для одного и того же зуба зависят от диаметра окружности, к которой они относятся. Условились для некоторой окружности, называемой делительной, выбирать модуль из ряда рациональных чисел (СТ СЭВ 310 76).
Делительную окружность можно определить как окружность, для которой модуль имеет стандартную величину, или же окружность, которая является базовой для определения размеров зубьев. Иногда начальные и делительные окружности совпадают (нулевые колеса), но при этом надо иметь в виду их принципиальное отличие. Делительная окружность есть характеристика одного зубчатого колеса, с которым она неизменно связана, и диаметр этой окружности имеет постоянную величину. Начальные окружности дают характеристику зацепления двух зубчатых колес, и диаметры этих
окружностей зависят от межосевого расстояния. На рис. 4.12 |
|
|
это окружности радиусов r1 и r2, проходящие через полюс |
|
|
зацепления W. В ряде случаев (см. ниже) радиусы начальных |
|
|
окружностей rW1 и rW1 равны r1 и r2 – радиусам делительных |
|
|
окружностей. |
|
|
Профиль каждого зуба нулевого колеса имеет часть, |
|
|
выступающую за делительную окружность и называемую |
|
|
|
а) |
|
начальной головкой зуба, и часть, находящуюся внутри |
|
|
окружности и называемую ножкой зуба (рис. 4.13). Так как |
|
|
размеры зубьев колеса одинаковы в торцевом сечении, то все |
|
|
головки зубьев внешнего зацепления ограничиваются |
|
|
снаружи окружностями вершин зубьев, их диаметры da1 и da2, |
|
|
а все ножки зубьев ограничиваются изнутри окружностями |
|
|
впадин зубьев, их диаметры df1 и df2. |
|
|
В случае внутреннего зацепления зубья колеса с |
|
|
внутренним расположением зубьев ограничиваются снаружи |
|
|
окружностью впадин, изнутри – окружностью вершин. |
|
|
Расстояние между окружностью вершин и делительной |
|
|
окружностью, измеренное по радиусу, носит название высоты |
|
|
|
б) |
|
головки зуба и обозначается через ha. Расстояние между |
|
|
окружностью впадин и делительной окружностью, |
|
|
|
|
|
измеренное по радиусу, носит название высоты ножки зуба и |
|
|
обозначается через hf. Таким образом, полная высота h зуба |
|
|
равна |
|
|
h = ha + hf. |
|
|
|
Рис. 4.13. Основные размеры |
|
107 |
зубчатых колес |
|
|
|
|

Дуга делительной окружности, вмещающая один зуб, носит название толщины зуба S. Дуга делительной окружности, вмещающая впадину, носит название ширины впадины l. Дуга делительной окружности, состоящая из одной толщины зуба и одной ширины впадины, называется шагом окружности р.
При передаче непрерывного движения двумя сопряжёнными колёсами шаг должен быть одинаков для обоих сопряжённых колёс.
Зубья колёс нарезаются на специальных станках режущим инструментом, размеры и форма которого зависят от величины модуля. Чтобы не иметь на машиностроительных заводах, изготовляющих зубчатые колёса, большие комплекты режущих инструментов, условились для делительной окружности выбирать модули из ряда рациональных чисел. Общесоюзным стандартом (ГОСТ 9563-60) установлены два ряда модулей, до которых должны округляться модули, получаемые из расчёта. В первом предпочтительном ряду предусмотрены следующие модули в мм: 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100.Во втором
ряду предусмотрены модули, промежуточные между модулями первого
Рис. 4.14. Картина зубчатого зацепления
ряда, например 3,5; 4,5; 5,5; 7; 9; 11 и др.
Определим основные размеры зубчатых колёс, у которых делительные окружности совпадают с начальными. Такие колёса будем называть нулевыми. Диаметры d1 и d2 делительных окружностей будут равны
d1 = 2r1 = mz1, d2 = 2r2 = mz2,
где z1 и z2 – соответственно число зубьев колёс 1 и 2. Высота головки зуба ha и высота ножки зуба hf обычно принимаются равными
ha = ha*·m и hf = hf*·m,
108
где коэффициент высоты головки зуба. Для колёс с неукороченной высотой ha*=1, для колёс с укороченной высотой ha*=0,8. Коэффициент высоты ножки зуба равен
hf* = ha*+с*,
где коэффициент радиального зазора для колёс с неукороченной высотой зуба с* = 0,25, для колёс с укороченной высотой зуба с* = 0,2.
Больший размер ножки по сравнению с головкой обеспечивает зазор между головкой зуба и впадиной. Тогда диаметры da1 и da2 окружностей вершин зубьев, а также диаметры df1 и df2 окружностей впадин (рис. 4.14) соответственно будут равны
da1 = d1 + 2ha, da2 = d2 + 2ha, df1 = d1 - 2hf, df2 = d2 - 2hf.
4.3.4. Построение эвольвентного зацепления
Построение эвольвентного зацепления (рис. 4.15) сводится к следующему.
По приведенным выше формулам при заданном числе зубьев z1 и z2 и модулю зацепления m подсчитывают межосевое расстояние, а также диаметры делительных окружностей, диаметры окружностей впадин и диаметры вершин зубьев колес.
Откладываем межосевое расстояние О1О2 и проводим перечисленные выше окружности. Рассчитываем радиусы основных окружностей как
rb1 = r1 / соsαw и rb2 = r2 / соsαw,
где αw – угол зацепления в сборке зубчатых колес. При нулевом зацеплении (см. ниже) αw = 20˚– стандартная величина угла зацепления.
109
