Линейная алгебра и аналитическая геометрия

Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

параллельна оси

(прямая совпадает с осью ).

(прямая совпадает с осью

(прямая совпадает с осью

.pdf

Скачиваний:

Добавлен:

27.08.2020

Размер:

3.47 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3414 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Линии на плоскости могут быть заданы не только в прямоуголь-


ной декартовой системе координат.
Пусть на плоскости задана полярная система координат.
Опр. Уравнение		,	с двумя переменными	называ-
ется уравнением линии			если этому уравнению удовлетворяют ко-
ординаты	любой точки , лежащей на линии , и не удовлетво-

ряют координаты любой точки, не лежащей на этой линии (рис. 3.12).

( , )

Рис. 3.12. Уравнение линии в полярной системе координат

Пример 4. Окружность радиуса R с центром в полюсе O (рис. 3.13).

Рис. 3.13. Полярное уравнение окружности

Пример 5. Лемниската Бернулли:				(рис. 3.14).

Рис. 3.14. Лемниската Бернулли

133

3.2. ПРЯМАЯ НА ПЛОСКОСТИ

3.2.1. Различные виды уравнений прямой на плоскости

В разделе 3.1 было показано, что любая прямая на плоскости может быть задана в произвольной прямоугольной декартовой систе-

ме координат	линейным уравнением относительно переменных
:
	, где	.

При этом коэффициенты и имеют простой геометрический смысл: это координаты вектора , перпендикулярного к данной прямой: . Такой вектор называется вектором нормали или нормальным вектором к данной прямой, а уравнение называется общим урав-

нением прямой.
1. Общее уравнение прямой на плоскости:
,	.

Прямую на плоскости можно задать и другими уравнениями, но эти уравнения всегда будут линейными относительно переменных

. Различные виды уравнений прямой на плоскости связаны с разными способами геометрического задания этой прямой.

Рассмотрим сначала частные случаи общего уравнения, когда один или два из коэффициентов , , равны нулю. В этом случае уравнение прямой называется неполным. Если все коэффициенты от-

личны от нуля	, то уравнение прямой называется полным.
2. Неполные уравнения прямой (рис. 3.15 – 3.17).
		.

Рис. 3.15. Прямая проходит через начало координат

134


	.
, где		.
, где		.

Рис. 3.16. Прямая

параллельна оси

		.

	, где		.
	, где		.

Рис. 3.17. Прямая

3. Уравнение прямой, проходящей через данную точку с данным вектором нормали (нормальное уравнение, см. рис. 3.18):

		.

,	.
— нормальный вектор,	.

135

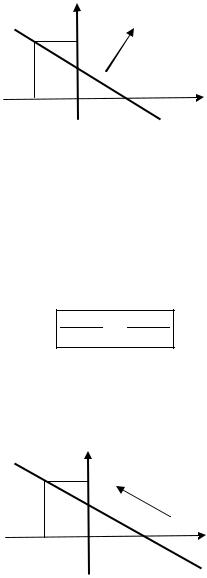
Рис. 3.18. Нормальное уравнение прямой

Вывод этого уравнения был сделан при доказательстве теоремы

2 (раздел 3.1.2).

4. Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение, см. рис. 3.19):

— направляющий вектор,

Рис. 3.19. Каноническое уравнение прямой

Вывод уравнения:	;	,
; необходимым и достаточным условием коллинеарности век-
торов является пропорциональность их координат, поэтому
		.

5. Параметрические уравнения прямой, проходящей через дан-

ную точку параллельно данному вектору (рис. 3.20).

, t

136

Рис. 3.20. Параметрические уравнения прямой

	Вывод уравнений:
		,		где	— некоторое число
(	);				.
	6. Уравнение прямой,	проходящей		через	две данные точки
(рис. 3.21).

			.
			.

		,			.

Рис. 3.21. Уравнение прямой, проходящей через 2 данные точки

	Вывод уравнения. Составим каноническое уравнение, где в ка-
честве направляющего вектора возьмем
(	,	), а в качестве точки	возьмем точку
(		).
			137

7. Уравнение прямой, отсекающей на осях координат заданные отрезки (уравнение прямой «в отрезках», см. рис. 3.22).

Рис. 3.22. Уравнение прямой «в отрезках»

Вывод уравнения. Составим уравнение прямой, проходящей че-

рез точки	и	:
			.
			.

8. Уравнение прямой с единичным вектором нормали и проходящей на заданном расстоянии от начала координат (нормированное уравнение, см. рис. 3.23).

			.

,	.	направлен в сторону прямой,
		.

Рис. 3.23. Нормированное уравнение прямой

138

Вывод уравнения. Расстояние от начала координат до прямой

равно ;	— единичный вектор нормали к прямой .
Для произвольной точки		выполнено условие:

		.

9. Уравнение прямой, проходящей через данную точку в данном направлении (уравнение прямой с угловым коэффициентом, см.

рис. 3.24).
		.
		.

,	tg ,	,

,— угловой коэффициент

Рис. 3.24. Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Вывод уравнения. Введем новую систему координат , полученную из параллельным переносом в точку и поворотом системы координат на угол . При этом начало новой системы коор-

динат	совпадает с точкой	(	), а ось	лежит на прямой
.
В	новой системе координат		прямая	задается уравнением

. По формулам (3.7) имеем:

		.
		.

Тогда

139


	tg	.

Замечание 1. Уравнением с угловым коэффициентом может быть задана любая прямая на плоскости, кроме прямой, параллельной

оси	.
Замечание 2. Уравнение:				можно привести к
виду	, где коэффициент равен ординате точки пересе-
чения прямой	с осью	(см. рис. 3.25).

				.

tg	,		, — угловой коэффициент.

Рис. 3.25. Уравнение прямой с угловым коэффициентом

Приведение различных видов уравнений прямой к общему виду

Все рассмотренные выше виды уравнений прямой на плоскости

легко приводятся к	общему уравнению:			,	где
. Покажем это.
Нормальное уравнение:
			, где		.
Каноническое уравнение:
Каноническое уравнение:
			, где	,	,
.
Параметрические уравнения:
Параметрические уравнения:
, где	,	,		.

140

Уравнение	в отрезках:
Уравнение	в отрезках:
	, где	,	,			.
Нормированное		уравнение:
	, где		,		,	.
Уравнение	с	угловым		коэффициентом:
					, где	,	,	.

Пример 1. Составить уравнение прямой, проходящей через две точки

и	и привести его к общему виду.
Уравнение прямой имеет вид:
		.

Пример 2. Составить уравнение прямой с угловым коэффициентом,

проходящей через точку	под углом	к оси , и при-
вести его к общему виду.

Вычислим угловой коэффициент:			. Уравнение

прямой имеет вид:		.

Возможна и обратная задача: приведение общего уравнения прямой к одному из видов уравнений, рассмотренных выше. Рассмот-

рим два случая.

Приведение общего уравнения к уравнению в отрезках

Пусть общее уравнение прямой — полное

тогда:

, где

Пример 3. Составить уравнение прямой в отрезках:

Сделать рисунок (см. рис. 3.26).

141

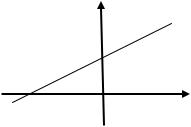
Рис. 3.26. К решению примера 3

Приведение общего уравнения к нормированному уравнению

Дано общее уравнение: ; чтобы привести его к нормированному виду, надо найти координаты единичного вектора

нормали

, где

. Разделим обе части общего уравне-

ния на

Учитывая, что в нормированном уравнении свободный член отрицателен, выбираем знак перед дробью противоположным знаку ко-

эффициента

в общем уравнении: « », если

и « », если

Выбрав знак по этому правилу, получим нормированное уравнение:

, где

Пример 4. Привести общее уравнение

к нормиро-

ванному виду.

Здесь

Учитывая, что

, выбираем

знак « » и делим обе части уравнения на

. Получим нормиро-

ванное уравнение:

Упр. 8. Составить полярное уравнение прямой, проходящей на заданном расстоянии p от полюса и образующей заданный угол с поляр-

ной осью.
Уравнение пучка прямых
Опр. Пучком прямых с центром в точке	называется множест-
во всех прямых на плоскости, проходящих через точку		(рис. 3.27)
142

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3414 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в папке Учебники

#
27.08.20203.23 Mб23Введение в мат.анализ.pdf
#
27.08.20203.47 Mб25Линейная алгебра и аналитическая геометрия.pdf