

Угол между плоскостями совпадает с углом между их векторами
нормали или дополняет этот угол до 180 ( |
. Так как |
|
|
, то достаточно вычислить косинус угла между |
|
векторами и взять полученное значение по модулю. |
|
|
Пусть даны общие уравнения плоскостей: |
|
|
: |
и : |
. |
|
Рис. 4.14. Угол между плоскостями |
|
|
|
|
|
|
|
|
|||||||||
Пусть — угол между плоскостями |
и |
(см. рис. 4.14). То- |
||||||||||||||||
гда справедлива формула: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Условие параллельности плоскостей: |
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
||||||||||||||
Условие |
перпендикулярности: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние от точки до плоскости |
|
|
|
|
|
|
|
|
|||||||||
Пусть дана плоскость |
в пространстве и точка |
|
|
|
|
. Тре- |
||||||||||||
буется найти расстояние |
от точки |
до плоскости : |
. |
|||||||||||||||
Рассмотрим два случая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1). Плоскость |
задана нормированным уравнением: |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
. Здесь — это расстояние от на- |
|||||||||||||||
чала координат до плоскости . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
193

|
|
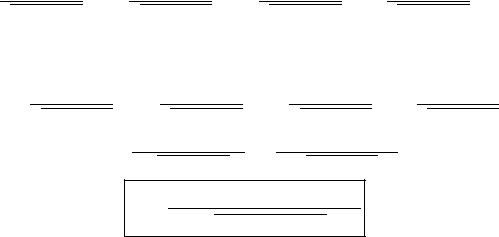
Рис. 4.15. Расстояние от точки до плос- |
|
|
|||||
|
|
кости (точки |
и |
лежат по разные |
|
|
|||
|
|
|
стороны от плоскости) |
|
|
|
|||
Расстояние |
равно модулю вектора |
, где точка |
— про- |
||||||
екция (основание |
перпендикуляра) точки |
на плоскость |
: |
||||||
|
. Рассмотрим проекцию вектора |
на единичный вектор |
|||||||
нормали |
. Числа |
, |
и |
связаны между собой. |
|
|
|||
Если точка |
и начало координат лежат по разные стороны от |
||||||||
плоскости |
, то |
|
|
(см. рис. 4.15). |
|
|
|||
Если точка |
и начало координат лежат по одну сторону от |
||||||||
плоскости |
, то |
|
|
(см. рис. 4.16). |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Рис. 4.16. Расстояние от точки до плоскости (точки и лежат по одну сторону от плоскости)
Таким образом, имеем равенство: |
. Следова- |
|
тельно, |
. |
|
194 |
|
|
Так как |
, то по- |
|
лучаем формулу: |
|
|
|
|
|
|
|
|
Из этой формулы следует, что для вычисления расстояния от точки до плоскости , заданной нормированным уравнением, надо
координаты точки |
подставить в левую часть нормированного урав- |
|
нения и взять значение по абсолютной величине. |
|
|
2). Плоскость |
задана общим уравнением |
. |
Приведем общее уравнение плоскости к нормированному уравнению:
.
Тогда, используя формулу для расстояния в случае нормированного уравнения, получим:
.
Из этой формулы следует, что для вычисления расстояния от
точки |
до плоскости , заданной общим уравнением |
|
, надо координаты точки подставить в левую часть об- |
щего уравнения и взять значение по абсолютной величине; затем по-
лученное выражение разделить на |
|
|
|
. |
|
|
|
|
||||||
Пример 1. Плоскость |
отсекает на осях координат |
, |
, |
отрез- |
||||||||||
ки |
. Найти косинусы углов между плоскостью |
|
и коорди- |
|||||||||||
натными плоскостями и расстояние |
от начала координат до этой |
|||||||||||||
плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим уравнение плоскости |
: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
, |
, |
. Обозначим углы между плоско- |
|||||||||||
стью |
и координатными плоскостями через , , |
: |
|
, |
||||||||||
|
, |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
195 |

|
Запишем уравнения координатных плоскостей и их нормальные |
||||||||||||||||||||||
векторы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
, |
; |
: |
|
, |
|
; |
: |
, |
||||||||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда: |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
, |
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Запишем уравнение плоскости |
в нормированном виде: |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Следовательно, |
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4.2.3. Различные виды уравнений прямой в пространстве
Прямая в пространстве, как и любая друга линия в пространстве, может быть задана либо системой двух уравнений (как пересечение двух поверхностей), либо параметрическими уравнениями.
1. Общие уравнения прямой в пространстве. |
|
||||
Прямая |
|
в пространстве может быть задана как линия пересе- |
|||
чения двух непараллельных плоскостей |
и |
(рис. 4.17). Пусть |
|||
плоскости |
и |
заданы общими уравнениями |
|
||
: |
|
, |
: |
|
, причем |
|
|
. |
Тогда прямая |
задается системой |
|
уравнений: |
|
|
. |
|
|
Рис. 4.17. Прямая как пересечение двух плоскостей
196

Итак, |
если |
, |
то |
: |
— общие уравнения прямой в простран-
стве.
2. Канонические уравнения прямой в пространстве.
Прямую в пространстве можно задать точкой, лежащей на этой прямой и направляющим вектором, параллельным данной прямой
(см. рис. 4.18).
, |
. — направляющий вектор |
прямой .
Рис. 4.18. Прямая, проходящая через данную точку с данным направляющим вектором
Вывод уравнений. Для произвольной точки |
|
|
|
выпол- |
||||||||||
няется следующее условие: |
|
|
|
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
— канонические уравнения прямой |
||||||
Итак, |
|
|
|
|
|
|
|
|||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
впространстве.
3.Параметрические уравнения прямой в пространстве.
Прямую в пространстве, проходящую через данную точку и с данным направляющим вектором, можно задать также и параметрическими уравнениями.
, |
. — направляющий вектор |
прямой .
197
Вывод уравнений. |
|
|
, где |
— некоторое число ( |
); |
|
|
|
|
|
. |
Параметрические уравнения прямой в пространстве:
, t |
. |
4. Уравнения прямой в пространстве, проходящей через две дан-
ные точки (рис. 4.19).
, |
. |
Рис. 4.19. Прямая, проходящая через две заданные точки
Вывод уравнений. Составим канонические уравнения прямой,
где в качестве |
направляющего |
вектора |
возьмем |
|
||||||||||||||||||
|
|
|
|
|
|
|
( |
|
|
|
, |
|
|
|
|
|
|
), а |
||||
в качестве точки |
|
|
|
возьмем точку |
( |
|
|
|
|
|
): |
|||||||||||
|
|
|
|
|
|
|
|
|
|
— уравнения прямой в пространстве, прохо- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
дящей через две точки. |
|
|
|
|
|
|
|
|
||||||||||||||
Пример 1. Уравнения прямой, проходящей через точки |
и |
|||||||||||||||||||||
|
|
|
, имеют вид: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
198
Переход от одних уравнений к другим
Уравнения прямой, проходящей через две точки, являются частным случаем канонических уравнений.
Параметрические уравнения прямой легко преобразуются в канонические уравнения и обратно:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Канонические уравнения прямой являются частным случаем |
|||||||||||||||||||||||||||||||||||||||||||||||||||
общих уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Рассмотрим систему уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Эта система зада- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
ет прямую в пространстве как пересечение двух плоскостей |
и |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
заданных неполными уравнениями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
задает плоскость |
, |
|
|
параллельную оси |
: |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
( |
); |
|
уравнение |
|
|
|
|
|
|
|
|
|
|
задает плоскость |
, |
па- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
раллельную оси |
: |
( |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Плоскости |
|
и |
|
|
|
проектируют прямую |
в пространстве на |
||||||||||||||||||||||||||||||||||||||||||||
координатные плоскости |
|
и |
|
|
, а |
уравнения |
|
|
|
|
|
и |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
являются уравнениями прямых |
и |
|
|
в этих коорди- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
натных плоскостях, т. е. являются уравнениями проекций прямой |
|
на |
||||||||||||||||||||||||||||||||||||||||||||||||||||
координатные плоскости (рис. 4.20). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
199

Рис. 4.20. Проекции прямой в пространстве на координатные плоскости
Аналогично, другие системы уравнений |
|
|
|
и |
|
|
|
|
|
, являются уравнениями проекций прямой |
на другие |
пары координатных плоскостей.
Поэтому канонические уравнения прямой в пространстве можно назвать еще и уравнениями прямой в проекциях на координатные плоскости.
Рассмотрим переход от общих уравнений прямой в пространстве к каноническим уравнениям.
: |
— общие уравнения прямой. |
Чтобы перейти к каноническим уравнениям, надо найти направляющий вектор прямой и точку , лежащую на этой прямой
(рис. 4.21).
Рис. 4.21. Прямая как пересечение двух плоскостей
200
Так как и |
|
, то и |
. Направляющий век- |
тор ортогонален векторам |
и , значит, его можно выразить че- |
||
рез векторное произведение этих векторов: |
|
||
Чтобы найти точку |
, лежащую на прямой |
, надо |
||
найти какое-нибудь решение системы уравнений |
|
|||
|
|
|
. |
|
Для этого, например, можно подставить вместо одной из пере- |
||||
менных |
|
какое-нибудь конкретное значение (например, |
, |
|
или |
, или |
) и решить систему двух линейных уравнений с |
||
оставшимися двумя неизвестными.
Если полученная система не имеет решений, то надо взять ка- кое-нибудь значение другой переменной и затем решить полученную
систему уравнений с оставшимися двумя неизвестными. |
|
Канонические уравнения одной и той же прямой |
могут быть |
различными за счет произвола в выборе точки |
на этой |
прямой. |
|
Пример 2. Составить канонические уравнения прямой, заданной об-
щими уравнениями |
|
. |
Здесь |
, |
. Найдем векторное произведе- |
ние этих векторов. |
|
|
. |
|
|
В качестве направляющего вектора |
можно взять |
вектор |
. Найдем точку |
на этой прямой. |
Пусть |
, тогда имеем систему уравнений: |
|
|
201
|
|
|
|
|
|
|
|
|
. Канонические уравнения |
|
прямой: |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
4.2.4. Основные задачи на прямую в пространстве
Взаимное расположение двух прямых в пространстве
Две прямые и в пространстве могут быть:
- совпадающими |
; |
- параллельными |
; |
- пересекающимися |
; |
- скрещивающимися |
. |
Задача состоит в том, чтобы по заданным уравнениям прямых определить их взаимное расположение в пространстве, найти угол между ними, а в случае пересекающихся прямых найти и точку их пересечения.
Для определенности считаем, что прямые |
и |
заданы кано- |
|||||||||||
ническими уравнениями: |
|
|
|
|
|||||||||
: |
|
|
|
|
|
, : |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
Тем самым |
заданы направляющие векторы |
этих прямых |
|||||||||||
, |
|
|
|
и точки на этих прямых |
|
|
|||||||
, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
1. Угол между прямыми в пространстве.
Если прямые параллельны или совпадают, то угол между ними
равен ( или |
радиан). Если прямые перпендикулярны, то угол |
||
между ними равен |
или |
|
радиан. Если прямые — пересекающие- |
|
|||
ся, но не перпендикулярны, то под углом между этими прямыми понимают острый угол между ними. Если прямые — скрещивающиеся, то под углом между этими прямыми понимают угол между пересекающимися прямыми, которые соответственно параллельны данным скрещивающимся прямым.
202
