Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4607 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)
Предмет:
Высшая математика
Файл:

ИЭ / 1 семестр / Учебники / Линейная алгебра и аналитическая геометрия

.pdf
Скачиваний:
25
Добавлен:
27.08.2020
Размер:
3.47 Mб
Скачать
☆

4. Составить уравнения сторон треугольника, зная одну из его вершин и уравнения высоты: и медианы:

проведенных из различных вершин (рис. П2.7).

 

 

 

 

 

Рис. П2.7.

— медиана,

 

—

 

 

 

 

 

 

 

высота,

— середина AB

 

 

 

 

Из уравнения высоты

 

 

 

 

найдем вектор норма-

ли

. Этот вектор является направляющим вектором стороны

AC. Составим уравнение стороны

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

Находим точку

— точку пересечения стороны

и медианы

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

Пусть

—

координаты точки

,

тогда

 

 

 

 

— координаты точки .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Точка

лежит на высоте

, а точка

лежит на медиане

, по-

этому координаты этих точек удовлетворяют уравнениям высоты и

медианы:

 

 

 

 

 

 

.

Решая эту

систему, получим:

 

 

 

. Уравнения

сторон

и

получим как

уравнения прямых, проходящих через две заданные точки.

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

333

:

 

 

 

 

 

.

 

 

 

 

 

Ответ: :

; :

;

 

 

 

 

 

:

.

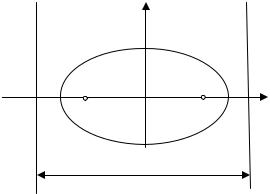
5. Вычислить эксцентриситет e эллипса, если известно, что расстояние между директрисами в 4 раза больше расстояния между фокусами

(рис. П2.8).

 

 

 

 

Рис. П2.8. К задаче № 5

 

 

— расстояние между

директрисами;

с — расстояние

между фокусами;

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:

.

6. Точка M лежит на параболе

и находится на расстоянии

9,125 от ее директрисы. Найти расстояние

от точки M до вершины

параболы (рис. П2.9).

 

 

 

 

 

 

 

 

 

— уравнение параболы,

— параметр параболы;

 

 

 

;

 

1,125.

 

 

 

 

 

 

 

 

 

 

 

M

— точка на параболе

;

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

Ответ:

.

334

9,125

r

 

 

 

 

 

 

 

Рис. П2.9. К задаче № 6

 

 

 

 

 

 

 

 

 

Ответы к варианту 2

 

 

1. [ ]:

 

 

 

; [ ]:

 

 

 

 

; [ ]:

 

.

2.

 

 

. 3.

 

 

 

. 4.

:

;

:

 

 

 

 

 

 

 

 

 

;

 

 

:

 

 

 

 

. 5. 90 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Аналитическая геометрия в пространстве

 

 

 

 

 

 

 

 

 

Вариант 1

 

 

1. Составить уравнение плоскости, проходящей через точку

 

 

параллельно векторам

.

 

 

 

 

 

Уравнение плоскости, проходящей через точку

 

 

перпендикулярно вектору нормали

, имеет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

Здесь в качестве вектора нормали

можно взять векторное про-

изведение векторов

 

 

 

 

 

:

 

 

.

Уравнение плоскости примет вид:

335

 

.

Ответ:

.

2. Составить канонические и параметрические уравнения прямой :

.

Прямая задана общими уравнениями, которые соответствуют способу задания прямой в виде пересечения 2-х плоскостей

(рис. П2.10).

O

Рис. П2.10. К задаче № 2

Эти плоскости заданы общими уравнениями, из которых можно найти координаты векторов нормали: .

Канонические и параметрические уравнения прямой в пространстве имеют следующий вид:

 

 

 

 

 

 

 

и

.

 

 

 

 

 

Здесь

 

— точка, лежащая на прямой;

— направ-

ляющий вектор прямой.

 

 

Для решения задачи нужно найти точку

и вектор . Чтобы

найти точку , надо найти какое-нибудь решение системы уравне-

ний:

. Эта система имеет бесконечное множест-

во решений;

пусть, например,

, тогда

,

. Таким об-

разом, точка

одна из точек, лежащих на прямой. В ка-

честве направляющего вектора , можно взять векторное произведение векторов и (т. к. и ).

336

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

. Составим канонические уравнения

прямой:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

. Составим параметриче-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ские уравнения прямой:

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Найти угол между прямой

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и плоскостью

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из

уравнений прямой

находим

ее

направляющий

вектор

.

 

Из

уравнения

плоскости находим ее вектор

нормали

 

 

 

 

. Угол между прямой и плоскостью можно найти из фор-

мулы: sin

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

,

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sin

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Найти точку M , симметричную точке M

 

 

 

 

 

Ответ:

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

относительно

прямой

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Проведем плоскость

 

через точку M перпендикулярно задан-

ной прямой:

 

 

 

 

 

, M

и найдем точку O — точку пересечения

прямой и плоскости (рис. П2.11).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В качестве вектора нормали плоскости

 

 

 

можно взять направ-

ляющий вектор заданной прямой

 

 

 

 

 

 

 

. Уравнение плоскости

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

337

 

 

.

M

M

Рис. П2.11. К задаче № 4

 

 

Найдем точку O:

 

 

 

 

. Чтобы решить эту сис-

тему, перейдем к каноническим уравнениям прямой:

 

и

подставим в уравнение плоскости:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

. Подставим найденное значение

в параметрические уравне-

ния:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

Найденная точка

является серединой отрезка MM ; зная коор-

динаты точек

и M, найдем координаты точки M .

 

 

 

 

;

 

 

 

;

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: M

.

338

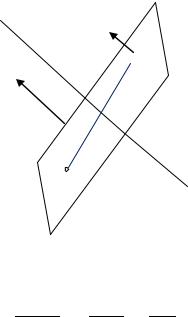
5. Найти расстояние между прямыми

 

 

 

 

 

и

 

 

 

.

Рис. П2.12. К задаче № 5

Чтобы вычислить расстояние между скрещивающимися прямы-

ми и

в пространстве, проведем плоскость

через прямую па-

раллельно прямой , затем найдем расстояние от точки

до плос-

кости

(рис. П2.12).

 

 

В качестве вектора нормали плоскости

можно взять вектор-

ное произведение направляющих векторов и

:

 

 

 

 

 

 

 

 

 

 

.

Составим

уравнение

плоскости

,

проходящей через точку

 

 

с вектором

нормали

 

:

 

 

 

 

 

.

 

 

Найдем

расстояние

от

точки

до

плоскости

по формуле:

 

 

 

 

. Подставляя координаты точки

в эту формулу,

 

 

 

 

 

 

 

получим:

.

Ответ: 13.

339

6. Найти сечение поверхности 2-го порядка

 

 

 

 

 

 

 

 

 

 

 

 

плоско-

 

 

 

 

 

 

 

 

 

 

 

стью

 

 

 

 

 

 

 

; определить параметры полученной линии.

 

 

 

 

 

 

 

 

 

 

Сечение поверхности плоскостью определяется из системы

уравнений:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Эта система задает сопряженную гиперболу в плоскости

,

параллельной координатной плоскости OXY, с полуосями

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: сопряженная гипербола в плоскости

 

 

 

 

 

 

 

с

полуосями

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы к варианту 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.

 

 

 

 

 

 

 

 

 

. 2.

 

. 3. arccos

 

. 4.

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.

 

 

. 6. эллипс в плоскости

 

 

с полуосями

 

 

 

 

 

 

 

и

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

340

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Фаддеев Д. К. Лекции по алгебре / Д. К. Фаддеев. — СПб.: Лань,

2007 — 416 с.

2.еклемишев Д. В. Курс аналитической геометрии и линейной ал-

гебры / Д. В. Беклемишев. — М.: Высшая школа, 1998 — 320 с.

3. Лобкова Н. И. Математика, том 1 / Н. И. Лобкова, Ю. Д. Максимов, Ю. А. Хватов. — СПб.: Изд-во Политехнического университета, 2007. — 454 с.

4. Ильин В. А. Линейная алгебра / В. А. Ильин, Э. Г. Позняк. — М.: Физматлит, 2007. — 278 с.

5. Ильин В. А. Линейная алгебра и аналитическая геометрия / В. А. Ильин, Г. Д. Ким. — Изд-во Проспект Московского университета,

2012. — 394 с.

6. Ефимов А. В. Сборник задач по математике для втузов. Ч. 1 / А. В. Ефимов [и др.]; под ред. А. В. Ефимова и А. С. Поспелова. — М.:

Физматлит, 2004. — 288

с.

 

7.

Письменный Д. Т. Конспект лекций по Высшей математике. 1

часть / Д. Т. Письменный. — М.: Айрис Пресс, 2011. — 288 с.

8.

Андрианов Ю.А.

Математика,

аналитическая геометрия /

Ю. А. Андрианов, Т. Н. Андрианова. —

СПб.: Изд-во Политехнического

университета, 2012. — 222 с.

 

9.

Цубербиллер О. Н. Задачи и упражнения по аналитической геомет-

рии / О. Н. Цубербиллер. — СПб., Лань, 2009. — 333 с.

341

Соседние файлы в папке Учебники
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности