Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Линейная алгебра и аналитическая геометрия

.pdf

Скачиваний:

Добавлен:

27.08.2020

Размер:

3.47 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3421 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

В любом случае угол между прямыми в пространстве либо равен углу между направляющими векторами этих прямых и , либо дополняет его до 180 (рис. 4.22).

Рис. 4.22. Угол между прямыми в пространстве

По известной формуле для косинуса угла между векторами получаем:

Условие параллельности прямых:			.
Условие параллельности прямых:			.
Условие перпендикулярности:
.
2. Условие принадлежности двух	прямых одной	плоскости

(рис. 4.23).

Рис. 4.23. Условие принадлежности двух прямых одной плоскости

Построим вектор			. Для принад-
лежности прямых	и	одной плоскости необходимо и достаточно,
чтобы векторы	,	,	были компланарны. Условием компла-

203

нарности векторов является равенство нулю их смешанного произведения:

При выполнении этого условия прямые и либо совпадают, либо параллельны, либо пересекаются. При невыполнении этого условия прямые и — скрещиваются.

В итоге приходим к следующему результату.

Взаимное расположение прямых и в пространстве зависит от значения ранга матрицы:

	.
Если	, то прямые скрещиваются; если	, то прямые
совпадают; если	, то прямые лежат в одной плоскости, а именно:
- при	— прямые параллельны,
- при	— прямые пересекаются.

Если прямые пересекаются, то точку пересечения прямых можно найти из системы уравнений:

Пример 1. Определить взаимное расположение прямых:

Здесь

и не совпадают. Проверим условие принадлежности

прямых одной плоскости:

, так как первая и третья строки пропорциональны.

204

Следовательно, прямые пересекаются. Найдем точку пересечения этих прямых:

. Перейдем к параметрическим уравнения прямых:

4.2.5. Основные задачи на прямую и плоскость в пространстве

Взаимное расположение прямой и плоскости в пространстве


Прямая	и плоскость в пространстве могут быть параллель-
ными	; прямая может пересекать плоскость в некоторой точке
; прямая может принадлежать плоскости		.

Задача состоит в том, чтобы по заданным уравнениям прямой и плоскости определить их взаимное расположение в пространстве, найти угол между ними и точку их пересечения.

Для определенности считаем, что прямая задана каноническими уравнениями, а плоскость задана общим уравнением:

:		, :	.
:		, :	.
Тем самым заданы: направляющий вектор			прямой ,
точка	на этой прямой и вектор нормали		к плоскости
.

1. Угол между прямой и плоскостью в пространстве (рис. 4.24).

205

	Рис. 4.24. Угол между прямой
	и плоскостью в пространстве
Пусть прямая	является проекцией прямой на плоскость

. Проекция прямой на плоскость — это множество всех оснований перпендикуляров, опущенных из точек прямой на плоскость.


	Опр. Углом	между прямой и плоскостью в пространстве на-
зывается угол между этой прямой и ее проекцией на эту плоскость.
	Если угол	между векторами	и	— острый, то он	равен
	(как на рис. 4.24), если угол — тупой, то он равен				.
	(как на рис. 4.24), если угол — тупой, то он равен				.

Поэтому по известной формуле для косинуса угла между векторами получим:

Получаем формулу для синуса угла между прямой и плоско-

стью:

Условие параллельности прямой и плоскости:

		.
Условие перпендикулярности прямой и плоскости:
			.
			.
2.	Пересечение прямой с плоскостью. Условие принадлежности
прямой	плоскости.

206

Если прямая не лежит в плоскости и не параллельна ей, то существует единственная точка их пересечения, которую можно най-

ти из системы уравнений: .

Чтобы решить эту систему, перейдем к параметрическим урав-

нениям прямой	:

			.

Подставляя найденное значение		в параметрические уравнения

прямой , получим координаты точки пересечения прямой с плоскостью.

Если	и	, то полу-
чим уравнение:	, которому удовлетворяет любое значение

параметра . Это означает, что любая точка прямой является точкой пересечения прямой и плоскости.

Таким образом, получили условие принадлежности прямой

плоскости

Пример 1.

Определить

взаимное расположение прямой

сти :

и :

Здесь

— направляющий

вектор прямой

— точка на этой прямой и

— вектор нормали

к плоскости .

Проверим условие параллельности прямой и плоскости:

, следовательно, прямая и плос-

кость пересекаются. Найдем угол между прямой и плоскостью.

26 .

207

Найдем точку пересечения прямой с плоскостью.

		точка пересечения.

4.3. ПОВЕРХНОСТИ 2-ГО ПОРЯДКА

Опр. Поверхность в пространстве называется поверхностью 2-го порядка, если она задается в некоторой прямоугольной декарто-

вой системе координат	алгебраическим уравнением 2-й степени
относительно переменных	:
	,
где	.

Как известно (теорема 3 из раздела 4.1.1), если поверхность в пространстве является поверхностью 2-го порядка в одной прямоугольной декартовой системе координат, то она остается поверхностью 2-го порядка и в любой другой прямоугольной декартовой системе координат.

Простейшим примером поверхности 2-го порядка является сфе-

ра, которая задается уравнением		. Рассмотрим дру-
гие поверхности 2-го порядка.
4.3.1. Цилиндрические поверхности
Пусть заданы в пространстве линия		и прямая . Через каждую
точку линии проведем прямую, параллельную прямой .
Опр. Множество точек	в пространстве, лежащих на прямых,
параллельных данной прямой	и пересекающих данную линию , на-

208

зывается цилиндрической поверхностью (или просто цилиндром). При этом прямая называется образующей, а линия — направляющей цилиндрической поверхности.

Другими словами, цилиндрическая поверхность — это поверх-

ность, образуемая движением прямой , перемещающейся в пространстве параллельно данной прямой и пересекающей данную линию

(рис. 4.25).

Обра ая цилиндра

а ра ля ая цилиндра

Рис. 4.25. Цилиндрическая поверхность

Рассмотрим цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой плоскости.

	1).	Пусть направляющая			лежит	в координатной плоскости
	и задается уравнением:				,	а образующая		параллельна
оси	:	,	(рис. 4.26).
	Составим уравнение цилиндрической поверхности .
	Для произвольной точки				найдем образующую, на которой
лежит эта точка, а на образующей найдем точку							, лежащую на на-
правляющей. Так как точки				и лежат на прямой, параллельной оси
,	то	у них совпадают		координаты		:	если	, то
		. Точка		, следовательно				. Таким обра-
зом,				.

209

вид:


Это означает, что если направляющая на плоскости			задает-
ся уравнением	, то цилиндрическая поверхность в про-
странстве задается таким же уравнением		. Так как в урав-
нение цилиндрической поверхности переменная		не входит, то зна-

чит, эта переменная может принимать произвольные значения.

Таким образом, уравнение цилиндрической поверхности имеет

Рис. 4.26. Цилиндрическая поверхность с образующей, параллельной

оси

2).	Пусть направляющая		лежит	в координатной плоскости
и задается уравнением:			,	а образующая параллельна
оси :	,	.

Аналогичными рассуждениями приходим к выводу, что в этом случае уравнение цилиндрической поверхности имеет вид:

			.
3).	Пусть направляющая		лежит	в координатной плоскости
и задается уравнением:			,	а образующая параллельна
оси :	,	.
В этом случае уравнение цилиндрической поверхности имеет
вид:	.

210

	Цилиндрические поверхности 2-го порядка
	Рассмотрим цилиндрические поверхности, направляющими ко-
торых являются кривые 2-го		порядка на координатной плоско-
сти	, а образующей является ось .
	Эллиптический цилиндр:		(см. рис. 4.27).

	Гиперболический цилиндр:		(см. рис. 4.28).

	Параболический цилиндр:		(см. рис. 4.29).

Рис. 4.27. Эллиптический цилиндр

	Рис. 4.28. Гиперболический	Рис. 4.29. Параболический
		цилиндр
	цилиндр

4.3.2. Конические поверхности

Пусть заданы в пространстве плоская линия и точка вне этой плоскости. Через каждую точку линии и точку проведем прямую.

Опр. Множество точек в пространстве, лежащих на прямых, проходящих через данную точку и пересекающих данную линию ,

называется конической поверхностью (или просто конусом). При этом

211

точка называется вершиной, линия — направляющей, а сами пря-

мые называются образующими конической поверхности.

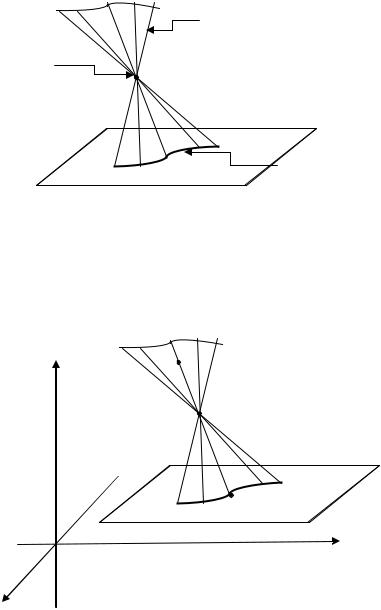
Другими словами, коническая поверхность — это поверхность, образуемая движением прямой, перемещающейся в пространстве так, что она постоянно проходит через неподвижную точку и пересекает данную линию (рис. 4.30).

Образующие

конуса

Вершина

конуса

Направляющая

конуса

Рис. 4.30. Коническая поверхность

Уравнение конической поверхности можно составить, если заданы уравнения направляющей и координаты вершины .

Рис. 4.31. Образующая

на конической поверхности

212

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3421 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в папке Учебники

#
27.08.20203.23 Mб23Введение в мат.анализ.pdf
#
27.08.20203.47 Mб25Линейная алгебра и аналитическая геометрия.pdf