Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Линейная алгебра и аналитическая геометрия

.pdf

Скачиваний:

Добавлен:

27.08.2020

Размер:

3.47 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 1617 / 3417 18 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

У сопряженной гиперболы действительная ось лежит оси , а

мнимая ось — на оси	. Поэтому фокусы лежат на оси , дирек-
трисы параллельны оси	. Асимптоты этих гипербол совпадают.

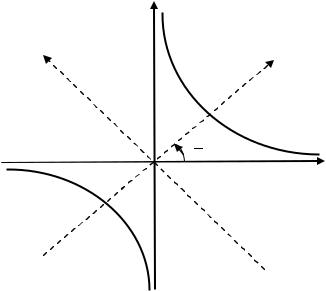
Ветви сопряженной гиперболы лежат в верхней и нижней (у основной гиперболы — в левой и правой) областях, на которые разбивают плоскость асимптоты гиперболы. Эксцентриситет сопряженной гиперболы .

Рис. 3.43. Сопряженная гипербола

Уравнение сопряженной гиперболы можно привести к каноническому виду путем поворота системы координат на угол .

Гипербола как график обратно-пропорциональной зависимости

Из элементарной алгебры известно, что гиперболой называется

график обратно-пропорциональной зависимости	. Покажем, что

два разных определения гиперболы не противоречат друг другу.
Рассмотрим линию, заданную уравнением		; пусть

(см. рис. 3.44).

163

Рис. 3.44. Гипербола, как график функции

Введем новую систему координат

, полученную из

по-

воротом осей координат на угол

. Формулы, связывающие ста-

рые и новые координаты, имеют вид (формулы (3.4)):

Подставим значения переменных

в уравнение линии

или

В новой системе координат

данная линия является равно-

сторонней гиперболой с полуосями

Параметрические уравнения гиперболы

Как и для эллипса, можно вывести параметрические уравнения

гиперболы:

164

где	—	гиперболический	косинус,
где	—	гиперболический	косинус,
	— гиперболический синус.
	— гиперболический синус.

3.3.3. Парабола

Опр. Параболой называется кривая 2-го порядка, определяемая в некоторой прямоугольной декартовой системе координат уравнением:

	,	.
Это уравнение называется каноническим уравнением параболы.
Число	из уравнения параболы называется параметром параболы.
Из уравнения следует, что парабола проходит через начало ко-
ординат	. Эта точка называется вершиной параболы.
Свойства параболы:
1. Парабола симметрична относительно оси		(оси параболы).

2. Парабола — неограниченная кривая и вся расположена в правой полуплоскости.

Упр. 11. Доказать свойства параболы.

Параболу можно построить, опираясь на ее свойства и исследуя ее каноническое уравнение (см. рис. 3.45).

Рис. 3.45. Парабола

Фокус и директриса параболы Опр. Точка , лежащая на оси параболы на расстоянии

от вершины, называется фокусом параболы.

165

Для произвольной точки параболы отрезок , а также его длина называются фокальным радиусом точки .

Опр. Прямая D, перпендикулярная оси параболы и проходящая на расстоянии от параболы (и от ее вершины), называется дирек-

трисой параболы.
Уравнение директрисы D:	.

Теорема 6 (фокально-директориальное свойство параболы). Для любой точки параболы расстояние от нее до фокуса равно расстоя-

нию до директрисы:		.
Доказательство. Пусть			— произвольная точка парабо-

лы. Найдем выражение для фокального радиуса через координаты точки :

Расстояние от точки

до директрисы:

Теорема доказана.

Замечание. По аналогии с гиперболой и эллипсом для параболы можно ввести понятие эксцентриситета так, чтобы выполнялось фо-


кально-директориальное свойство:	. Но так как для параболы

, то эксцентриситетом параболы должна быть единица:		.

Пример 1. Найти параметр, фокус и уравнение директрисы параболы,


заданной уравнением:		. Сделать рисунок (см. рис. 3.46).
Каноническое уравнение параболы:			.	Следовательно:
,	, фокус	, уравнение директрисы D:		.

166

Рис. 3.46. К решению примера 1

Разновидности канонического уравнения

Кроме канонического уравнения могут рассматриваться и другие «простейшие» уравнения, которые также задают параболу (см. рис. 3.47):

Рис. 3.47. Разновидности канонического уравнения параболы

Все эти уравнения можно привести к каноническому виду в новой системе координат путем поворота старой системы координат на углы соответственно:

3.3.4. Общие свойства кривых 2-го порядка

Рассмотрим некоторые свойства, которые являются общими для изученных нами кривых 2-го порядка: эллипса, гиперболы и параболы.

167

Фокально-директориальное свойство кривых 2-го порядка

Пусть на плоскости задана некоторая прямая и точка вне этой прямой (рис. 3.48). Тогда множество точек на плоскости, для которых отношение расстояний от них до точки к расстояниям до прямой есть величина постоянная и равная некоторому числу ,

представляет собой:
эллипс, если	;
гиперболу, если	;
параболу, если	.

Рис. 3.48. Фокально-директориальное свойство кривых 2-го порядка

Полярные уравнения кривых 2-го порядка

Для окружности радиуса R с центром в полюсе O полярное

уравнение имеет вид:

(рис. 3.49).

Рис. 3.49. Полярное уравнение окружности

Рассмотрим полярные уравнения других кривых 2-го порядка. Для каждой из кривых 2-го порядка, отличной от окружности,

введем полярную систему координат по следующему правилу.

168

Полюс полярной системы координат совместим с фокусом (для эллипса и гиперболы — с одним из фокусов), полярную ось направим перпендикулярно к директрисе в сторону, противоположную ей (для эллипса и гиперболы — противоположную директрисе, соответствующей выбранному полюсу).

Обозначим через расстояние от фокуса до директрисы :

(рис. 3.50).

Рис. 3.50. Полярное уравнение кривых 2-го порядка

Cогласно фокально-директориальному свойству для всех точек

кривой 2-го порядка выполняется равенство:			. Расстояние от

точки до директрисы равно	.
Подставляя это выражение в формулу		, получим:

				.

Полярное уравнение кривых 2-го порядка:

Если , то полярное уравнение задает эллипс. Если , то полярное уравнение задает гиперболу (только одну ее ветвь). Для па-


раболы (	) полярное уравнение имеет вид:		. Напри-

мер, полярное уравнение		задает параболу с параметром

и с каноническим уравнением		.

169

Пример 1. Выяснить, какие кривые задаются полярными уравнения-

ми: а)

, б)

а)

уравнение эллипса;

б)

уравнение гипербо-

лы.

Уравнения касательных к кривым 2-го порядка

Теорема 7. Уравнение касательной к кривой 2-го порядка, про-

ходящей через точку

, имеет вид:

для эллипса

;

для гиперболы

;

для параболы

Упр. 12. Доказать теорему 7.

Оптические свойства кривых 2-го порядка

1. Луч света, выходящий из одного фокуса эллипса, после зер-

кального

отражения от

эллипса проходит

через другой его фокус

(рис. 3.51).

касател ная

Рис. 3.51. Оптическое свойство эллипса

2. Луч света, выходящий из одного фокуса гиперболы, после зеркального отражения от гиперболы проходит так, что кажется выходящим из другого ее фокуса (рис. 3.52).

170

касательная

Рис. 3.52. Оптическое свойство гиперболы

3. Луч света, выходящий из фокуса параболы, после зеркального отражения от параболы проходит параллельно ее оси (рис. 3.53).

касательная

Рис. 3.53. Оптическое свойство параболы

Доказательство этих свойств основано на использовании закона «угол падения равен углу отражения» и уравнений касательных к указанным кривым.

Упр. 13. Доказать оптические свойства кривых 2-го порядка.

3.3.5. Исследование общего уравнения кривых 2-го порядка

По определению кривая 2-го порядка — это линия на плоскости, которая задается в некоторой прямоугольной декартовой системе ко-

ординат	уравнением 2-й степени относительно переменных	:
	, где	.

171

При переходе к новой прямоугольной декартовой системе координат уравнение кривой остается уравнением 2-й степени относительно новых переменных (теорема 3 из раздела 3.1.2).

Классификация кривых 2-го порядка Опр. Уравнение кривой 2-го порядка называется уравнением эл-

липтического типа, если в некоторой прямоугольной декартовой системе координат оно имеет один из видов:

		,	(3.8)

		,	(3.9)

	.		(3.10)

При этом уравнение (3.8) задает эллипс (при			задает ок-

ружность); уравнение (3.9) задает вырожденный эллипс (точку); уравнение (3.10) задает мнимый эллипс (пустое множество).

Опр. Уравнение кривой 2-го порядка называется уравнением гиперболического типа, если в некоторой прямоугольной декартовой

системе координат оно имеет один из видов:
	,	(3.11)

	.	(3.12)

При этом уравнение (3.11) задает гиперболу; уравнение (3.12) задает вырожденную гиперболу (пару пересекающихся прямых).

Опр. Уравнение кривой 2-го порядка называется уравнением параболического типа, если в некоторой прямоугольной декартовой

системе координат оно имеет один из видов:
,	(3.13)
,	(3.14)
,	(3.15)
.	(3.16)

При этом уравнение (3.13) задает параболу; уравнения (3.14) и (3.15) задают вырожденную параболу (пару параллельных прямых и

172

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 1617 / 3417 18 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

Соседние файлы в папке Учебники

#
27.08.20203.23 Mб23Введение в мат.анализ.pdf
#
27.08.20203.47 Mб25Линейная алгебра и аналитическая геометрия.pdf