
Для произвольной точки |
в пространстве вектор |
на- |
||
зывается радиус-вектором точки |
. Вектор |
можно разложить по ба- |
||
зису { |
}: |
|
|
|
|
, где |
, |
, |
. |
Прямоугольными декартовыми координатами точки M в про-
странстве называются координаты ее радиус-вектора относительно
ОНБ { |
}. Обозначение: M ( |
). |
|
|
|
|
|
|
|
|
|
, |
, |
. |
Произвольный вектор |
в пространстве можно разложить по |
|||
ортонормированному базису: |
, где |
, |
||
|
, |
. |
|
|
Теорема 2. Координаты вектора в пространстве равны разностям
соответствующих координат конца и начала этого вектора: |
|
|
. |
Доказательство этой теоремы проводится аналогично доказательству теоремы 1.
2.3.2. Действия с векторами в прямоугольной декартовой системе координат
1. Линейные действия. |
|
|
||
Пусть |
даны |
координаты векторов |
и |
относительно ОНБ |
{ }: |
, |
. Тогда: |
|
|
-при умножении вектора на число все его координаты умножаются на это число;
-при сложении (вычитании) векторов соответствующие координаты складываются (вычитаются):
λ |
; λ |
; |
; |
.
103
Условие коллинеарности векторов на плоскости |
|
|||||
в координатной форме |
|
|||||
Векторы |
и |
коллинеарны тогда и только то- |
||||
гда, когда их координаты пропорциональны: |
|
|||||
|
|
|
|
|
rang |
. |
|
|
|||||
Пусть даны координаты векторов |
и относительно ОНБ { |
}: |
||||
, |
|
. Тогда: |
|
|
||
-при умножении вектора на число все его координаты умножаются на это число;
-при сложении (вычитании) векторов соответствующие координаты складываются (вычитаются):
λ |
|
; λ |
|
|
|
|
; |
|
|
|
; |
|
|
|
|
|
. |
||
Условие коллинеарности векторов в пространстве |
|
||||||||
|
в координатной форме |
|
|
||||||
Векторы |
и |
|
|
коллинеарны тогда и толь- |
|||||
ко тогда, когда их координаты пропорциональны: |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
. |
|||
2. Произведения векторов. |
|
|
|
|
|
|
|||
Теорема. Для векторов |
, |
|
|
, |
, |
||||
заданных в ОНБ { |
}, справедливы формулы вычисления скаляр- |
||||||||
ного, векторного и смешанного произведений:
|
; |
; |
. |
104

Если векторы |
, |
, |
заданы в ОНБ |
{ }, то |
; |
; |
. |
Доказательство. Используем «таблицы скалярного и векторно- |
|||
го умножений» векторов из ОНБ { |
: |
|
|
1 0 0
0 1 0
0 0 1
, |
, |
. |
.
.
( )
.
Формулы для векторов, заданных в ОНБ { }, вытекают из по-
лученных формул при |
. Теорема доказана. |
|
105 |
Пример 1. |
, |
, |
. |
;
Следствие 1 (геометрический смысл определителей 2-го и 3-го
порядка). |
|
|
|
|
|
|
1) Определитель 2-го порядка |
|
с точностью до знака |
||
равен площади параллелограмма, построенного на векторах |
|||||
и |
: |
, причем знак « » означает, что пара векторов |
|||
|
— правая, а знак « » означает, что пара векторов |
— ле- |
|||
вая. |
|
|
|
|
|
|
2) Определитель 3-го порядка |
|
с точностью до |
||
знака |
равен объему |
параллелепипеда, построенного |
на векторах |
||
|
, |
и |
: |
, |
причем знак |
« » означает, что тройка векторов |
|
— правая, а знак « » оз- |
|||
начает, что тройка векторов |
— левая. |
|
|||
|
Доказательство. 1) |
|
|
; |
|
|
|
|
. По определению векторного |
||
произведения тройка векторов |
— правая. |
|
|||
106 |
|
|
|
|
|
Если |
, |
то |
; следовательно, со стороны вектора |
|||
движение от вектора к вектору |
видно против часовой стрелки, |
|||||
т. е. пара векторов |
— правая. |
|
|
|
||
Если |
, |
то |
; следовательно, со стороны вектора |
|||
движение от вектора |
к вектору видно против часовой стрел- |
|||||
ки, а значит со стороны вектора |
движение от вектора |
к вектору |
||||
видно по часовой стрелке, т. е. пара векторов |
— левая. |
|||||
2) |
|
; |
|
|
|
; |
|
— правая тройка; |
|
|
— левая тройка. След- |
||
ствие 1 доказано.
Следствие 2 (условия ортогональности, коллинеарности и ком-
планарности векторов). |
|
|
|
|
Для векторов |
, |
, |
, задан- |
|
ных в ОНБ { |
}, выполнено: |
|
|
|
|
|
|
(условие ортогональности); |
|
|
|
(условие коллинеарности); |
|
|
, , — компланарны |
(условие компла- |
нарности).
Доказательство.
; ; , , — компланарны
. Далее используются формулы из теоремы. Следствие 2 до-
казано. |
|
|
|
|
Пример 2. Определить, при каких значениях λ векторы |
и |
будут |
||
ортогональны, если |
, |
, а векторы |
и |
зада- |
|
|
|
|
107 |
ны своими координатами |
относительно ОНБ { |
}: |
, |
|||||
. |
|
|
|
|
|
|
|
|
|
|
( |
) ( |
) |
|
|
|
|
|
4 |
|
|
|
|
λ2; |
||
|
|
|
|
λ2 |
|
|
; |
|
( |
2) |
|
( 2 ) |
2 |
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||
Пример 3. Определить, при каких значениях |
векторы |
, , |
будут |
|||||
компланарны, если они заданы своими координатами относительно
ОНБ { |
}: |
, |
, |
. |
|
, , |
компланарны |
|
|
|
|
2 |
1 |
|
2 |
|
|
|
2.3.3. Полярная система координат на плоскости |
|
|||
Возьмем на плоскости точку O и луч |
, исходящий из точки O. |
||||
На луче |
укажем направление от точки O и выберем масштаб. Точка |
||||
O называется полюсом, а луч — полярной осью. Тем самым введена |
|||||
полярная система координат на плоскости. |
|
|
|||
Для произвольной точки |
на плоскости полярными координа- |
||||
тами называются: полярный радиус |
и полярный угол |
, об- |
|||
разованный отрезком |
и полярной осью |
, отсчитываемый против |
|||
часовой стрелки (рис. 2.40). |
|
|
|
||
( , )
Рис. 2.40. Полярные координаты точки на плоскости
108
Естественные ограничения на полярные координаты: ,
. При этих ограничениях устанавливается взаимно-однозначное соответствие между точками на плоскости, кроме полюса, и упорядоченными парами действительных чисел (при .
Связь между полярными и прямоугольными координатами
Введем прямоугольную декартову систему координат следующим образом: начало координат поместим в полюс O, ось абсцисс совместим с полярной осью .
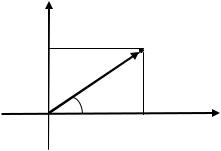
Пусть произвольная точка на плоскости имеет прямоугольные координаты и полярные координаты . Установим связь между этими координатами (рис. 2.41).
Рис. 2.41. Связь между полярными и прямоугольными координатами точки
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
, |
, |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
Чтобы определить полярный угол |
, надо установить (по знакам |
||||||||
) четверть, в которой лежит искомый угол, и учесть ограничения |
|||||||||
. |
|
|
|
|
|
|
|||
|
|
|
|
||||||
Пример 1. Найти полярные координаты точки |
|
. |
|||||||
|
|
|
|
|
|
|
|
109 |
|

|
|
|
|
|
|
|
|
|
|
|
Найдем |
: |
|
, |
|
|
|
|
, |
||
|
|
|
||||||||
. Учитывая, что точка |
лежит в 3-й четверти (рис. 2.42), полу- |
|||||||||
чим: |
. |
|
|
|
|
|
|
|
|
|
Таким образом: |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
Рис. 2.42. К решению примера 1 |
|
|
||||||||||
Пример 2. Точки |
и N заданы полярными координатами: |
|
, |
||||||||||||||
|
|||||||||||||||||
|
|
|
|
. Найти их прямоугольные координаты. |
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Для точки |
|
|
: |
|
|
|
|
|
; для точки |
: |
||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Следовательно: , .
2.3.4. Цилиндрическая и сферическая системы координат в пространстве
Цилиндрическая система координат в пространстве определя-
ется заданием плоскости с введенной на ней полярной системой ко-
ординат и осью |
, перпендикулярной к этой плоскости и проходя- |
||
щей через полюс O (рис. 2.43). |
|
||
В цилиндрической системе координат положение точки опре- |
|||
деляется тремя числами: |
и , где |
— полярные координаты |
|
точки проекции точки |
на заданную плоскость, а — координа- |
||
110 |
|
|
|

та на оси |
точки пересечения плоскости, параллельной данной и |
||
проходящей через точку , с осью |
. Обозначение: |
. |
|
Рис. 2.43. Цилиндрические координаты точки в пространстве
Связь между цилиндрическими и прямоугольными координатами
Введем прямоугольную декартову систему координат в пространстве следующим образом: начало координат поместим в полюс O, ось абсцисс совместим с полярной осью , ось аппликат совместим с осью , а ось ординат направим так, чтобы получилась правая система координат.
Тогда прямоугольные координаты , произвольной точки связаны с цилиндрическими координатами следующими равенствами:
, , , .
Сферическая система координат в пространстве может быть определена с помощью прямоугольной декартовой системы коорди-
нат |
в пространстве. Для этого достаточно задать оси |
и , а |
||||
также плоскость |
. |
|
|
|
|
|
|
Для произвольной точки |
в пространстве сферическими коор- |
||||
динатами называется тройка чисел |
, где |
|
— поляр- |
|||
ный радиус, — угол между отрезком |
и осью |
, — угол ме- |
||||
жду отрезком |
и осью , а |
— проекция точки |
на плоскость |
|||
|
(см. рис. 2.44). |
|
|
|
|
|
|
|
|
|
|
|
111 |

Ограничения на сферические координаты: |
, |
, |
. |
|
|
Рис. 2.44. Сферические координаты точки в пространстве
Связь между сферическими и прямоугольными координатами
Для произвольной точки пространства связь между ее прямоугольными и сферическими координатами дается следующими равенствами:
, , , .
Пример 1. Найти сферические координаты точки , равноудаленной |
||||
от осей координат |
, , |
и находящейся на расстоянии |
|
от |
|
||||
этих осей. |
|
|
|
|
Если точка равноудалена от осей координат, то |
. |
|||
Подставим вместо |
их выражения через сферические координа- |
|||
ты:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
112
