ИЭ / 1 семестр / Учебники / Линейная алгебра и аналитическая геометрия

Пусть

направляющая

задана

системой

уравнений

, а точка

— вершина конуса.

Возьмем на

поверхности

конуса

произвольную точку

. Образующая,

проходящая через точки

и

, пересечет направляющую

в некото-

рой точке

(см. рис. 4.31).

Координаты

точки

удовлетворяют системе

уравнений

. Канонические уравнения образующих, проходя-

щих через точки

и

,

имеют вид:

.

Исключая

из

системы

уравнений

,

получим

уравнение, связывающее переменные

. Это уравнение и будет

уравнением конической поверхности.

Пример 1. Составить уравнение конуса с вершиной в точке

,

если направляющей

служит эллипс

, лежащий в плоско-

сти

(рис. 4.32).

Составим систему уравнений

. Из равенств

и

получим:

,

. Подставляя значения

в

уравнение эллипса, получим:

. Это и

Конус 2-го порядка:

. При

получаем круговой

конус:

, где

.

же плоскости. Рассмотрим вращение линии

вокруг оси, совпадаю-

щей с прямой .

Опр. Поверхность

в пространстве,

образованная вращением

плоскости

вокруг оси . Пусть линия задана системой уравне-

ний

.

Пусть

— произвольная точка на поверхности враще-

ния . Проведем через точку

плоскость,

перпендикулярную оси

. Пусть

— точка пересечения этой плоскости с осью ,

—

точка пересечения этой плоскости с линией

. Эти точки имеют коор-

динаты:

,

.

Отрезки

и

являются радиусами одной и той же окруж-

ности, поэтому

.

Так как

,

, то

.

Точка

лежит на линии ,

поэтому ее координаты удовлетво-

ряют уравнению линии:

.

Таким образом,

уравнение поверхности вращения линии

во-

круг оси

имеет вид:

.

Это уравнение получено из уравнения линии

заме-

ной переменной

на

.

Аналогично доказывается, что при вращении этой же линии во-

круг оси

уравнение поверхности вращения будет иметь вид:

.

Если же линия

лежит в плоскости

, задана системой урав-

нений

и вращается вокруг оси

, то уравнение поверх-

ности вращения имеет вид:

.

Пример 1.

Составить

уравнение

поверхности вращения прямой :

вокруг оси

(рис. 4.34).

Заменим в уравнении прямой переменную на

:

.

215

Пусть дан эллипс в плоскости

:

. Вращаем эл-

менной в уравнении эллипса на

:

.

.

Трехосный эллипсоид:

, где

— полуоси эл-

превращается в

эллипсоид

вращения;

если все

полуоси

равны:

, то он превращается в сферу

.

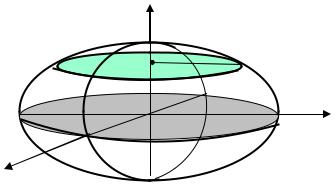
Рассмотрим сечения эллипсоида плоскостями, параллельными

координатным плоскостям:

,

,

.

.

Если

, то

значит, уравнение задает пустое

множество;

если

, то

и уравнение задает точку

.

Пусть

; обозначим:

; тогда

— это уравнение

эллипса с полуосями

и .

костями

и

.

4.3.5. Гиперболоиды

Пусть дана гипербола в плоскости

:

.

Если вращать гиперболу вокруг мнимой оси (оси

), то полу-

в уравнении гиперболы на

:

.

переходит в точку

, где

,

.

Подвергнем однополостный гиперболоид вращения равномер-

ному сжатию (растяжению) к плоскости

. Полученная поверх-

.

Однополостный гиперболоид (рис. 4.37):

.

Рассмотрим сечения однополостного гиперболоида плоскостя-

ми, параллельными координатным плоскостям:

,

,

.

,

где

. Таким образом, в сечении однополостного гипербо-

лоида плоскостями

получаем эллипсы.

218

.

При

, где

, это уравнения гипербол (основной

и сопряженной). Если

, то

— это пара пе-

ресекающихся прямых.

.

При

, где

это уравнения гипербол (основной

и сопряженной). Если

, то

— это пара пе-

Пусть дана гипербола в плоскости

:

.

в уравнении гиперболы на

:

параллельными координатным плоскостям:

,

,

.

220

. Если

, то

,

и

значит

уравнение

задает пустое

множество;

если

,

то

и уравнение задает точку

.

Пусть

; обозначим:

; тогда

— это уравнение

эллипса с полуосями

и .

Таким образом, в сечении двуполостного гиперболоида плоско-

стями

, где

, получаем эллипсы.

,

где

.

,

где

костями

,

получаем гиперболы.

4.3.6. Параболоиды

Рассмотрим параболу в плоскости

:

,

. Вра-

надо заменить переменную

в уравнении параболы на

:

.

дом с уравнением:

, где

.