5.2.1.3. Среднее значение и дисперсия характеристик качества регулирования

Характеристики (5.30) и (5.31) удобно представить в виде суммы среднего значения и дисперсии. Среднее значение, отражающее детерминированную часть, определяется в виде математического ожидания соответствующей характеристики:

, ,. (5.34)

Величина среднего значения (5.34) вычисляется с помощью (5.29) и (5.33), при этом стохастические составляющие эталонного воздействия и возмущений,заменяются своими средними значениями. В качестве начального состояния принимаются средние значения вектора.

Обозначим: ,– средние значения, а,– отклонения от них, т.е.

, .

Тогда среднее значение квадрата ошибки и входной переменной может быть представлено в виде:

, (5.35)

, (5.36)

где ,,– заданные неотрицательно определенные () весовые матрицы .

Будем считать, что ,– диагональные, тогда (5.35), (5.36) дают математическое ожидание суммы квадратов отклонений компонент соответствующих векторов.

5.2.1.4. Передаточные функции замкнутой системы

Выражения для вычисления иможно получить следует из объединенного описания замкнутой системы (5.27). Важнейшими являются передаточные функции с управляющего воздействия на выходные и измеряемые величины и с эталонной величины на измеряемые выходные величины и управления. Именно к эти м передаточным функциям приводится описание замкнутой системы (5.27). Взаимосвязь этих функций демонстрируется приведенной ниже на рис.5.3 схемой.

Рис. 5.3. Блок-схема замкнутой системы

(5.37)

(5.38)

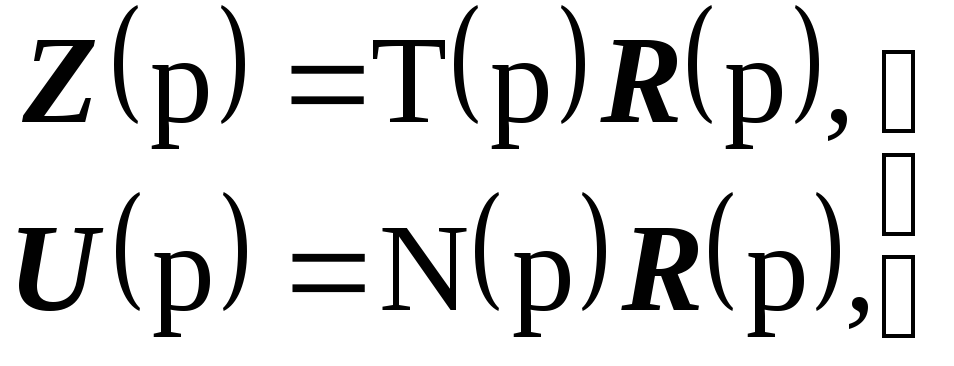(5.39)

где

(5.40)

(5.41)

В (5.38)-(5.39) курсивом обозначены изображения по Лапласу векторов входных и выходных величин. Важно отметить, что передаточные функции K(p),Т(р) иN(p) жестко взаимосвязаны, так что нельзя независимо изменить одну из них. Значения введенных характеристик качества (5.35), (5.36) в конечном итоге зависят от передаточных функций (5.40), (5.41), от расположения корней их характеристических уравнений на комплексной плоскости. Вследствие взаимосвязанности передаточных функций при синтезе управления необходимо найти компромисс между противоречивыми требованиями.

5.2.2. Примеры анализа стохастических систем

5.2.2.1. Реакция линейной системы стохастические внешние воздействия

Теорема . Пусть линейная система с матричной импульсной переходной функцией K(t, τ) находится в моментt₀в нулевом состоянии. Пусть входное воздействие на систему есть реализация стохастического случайного процессаu(t) со среднимm_u(t) и ковариационной матрицейR_u(t₁,t₂). Тогда выходные величины системы есть реализация стохастического процессаy(t) со средним:

(5.42)

и ковариационной матрицей:

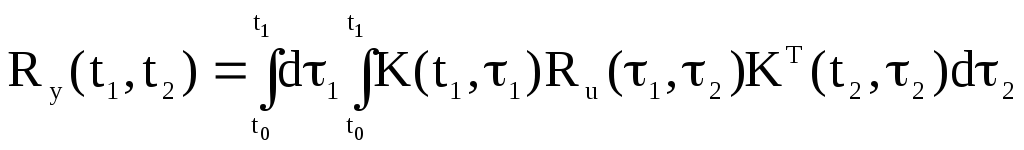(5.43)

при условии, что интеграл существует.

Так как выход описывается

(5.44)

то имеем

Теорема. Предположим, что линейная система с постоянными коэффициентами является асимптотически устойчивой и имеет матричную переходную функцию K(t-τ) и входной процессu(t) является стационарным в широком смысле с ковариационной матрицейRu(t₁-t₂). Тогда, если входное воздействие на систему является реализацией процессаu(t), который приложен с момента -∞, выходная переменная является реализацией стационарного в широком смысле стохастического процессаy(t) с ковариационной матрицей

. (5.46)

Теорема. Рассмотрим асимптотически устойчивую линейную систему с постоянными параметрами и матричной передаточной функцией H(p). Предположим, что входная переменная стационарного в широком смысле стохастического процессаu(t) с матричной спектральной плотностью, который приложен в момент времени -∞. Тогда выходная переменная является реализацией стационарного в широком смысле стохастического процессаy(t) с матричной спектральной плотностью

. (5.47)

Это преобразование Фурье предыдущего (5.46) выражения после замены t₁–t₂на τ и использования того, чтоH(p) есть преобразование Лапласа отK(τ).