3.2. Управление и стабилизация (Лекция 11)

3.2.1. Цель управления, идеальное управление

3.2.1.1. Общая схема разомкнутого и замкнутого управления

Общую схему объекта и системы управления можно представить в виде

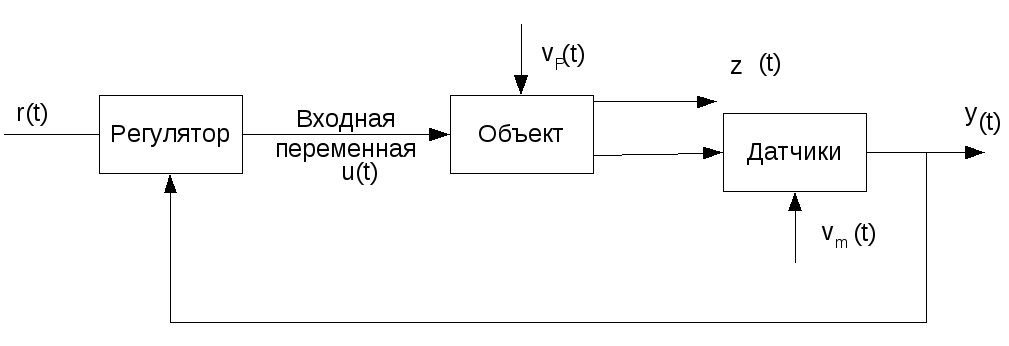
Рис.3.3. Схема объекта с замкнутым регулятором.

r(t) – эталонная переменная (заданное, желаемое значение управляемой переменнойz),y(t) – наблюдаемая переменная,v_P(t) – возмущающая переменная,v_m(t) - шум наблюдений,u(t) – управление(управляющая переменная).

Цель управления.

Целью управления является максимально точное выполнение условия:

z(t)r(t),tt₀(3.11)

Разомкнутыйрегулятор имеет место, еслиy(t) не подаётся в регулятор

u(t) =f_p[r(),t₀t],tt₀(3.12)

Если выходная переменная измеряется(наблюдается), её значение целесообразно использовать при определении управления.

Замкнутыйрегуляторu(t) =f_з[r(),t₀t;y(),t₀t],tt₀(3.13)

Объект + регулятор = система управления.

Будем считать y(t) = z(t), т.е. мы наблюдаем именно управляемую переменную, r(t) - заданное значение выходной переменной.

Если необходимо обеспечить, чтобы y(t)r(t),tt₀, гдеr(t) изменяемое во времени значение входной величины, то имеет место задачаслежения.

Если входная величина является постоянной r(t) =r₀tt₀, то имеет место задача регулирования, стабилизации.

3.2.1.2. Идеальное управление

Пусть (t) = y(t) - r(t), (3.14)

где (t) – ошибка слежения.

В случае

(t) = 0tt₀(3.15)

управление идеальное. В этом случае говорят, что система инвариантна по отношению к действующим возмущениям. Пусть объект описывается линейными дифференциальными уравнениями. Воспользуемся для краткости записи дифференциальных уравнений оператором дифференцирования, введенным в п.п. 2.3.1.1. , т.е. запишем их в виде (2.20). Так как мы будем определять управление, то разделим на две составляющие вектор w(t) = [u(t),v(t)], а именно на управлениеu(t) и возмущениеv(t). Тогда уравнения для состояний и для выходных переменных системы можно записать в виде

y(t) =(D)x(t)

Подставляя 1-е во 2-е, находим для выходной (управляемой) переменной выражение

(D)y(t) =(D)u(t) +(D)v(t), (3.16)

где ,,- многочлены от оператора дифференцирования, которые выражаются через,,,.

Подставим (3.14) в (3.16):

(D)[r(t) +(t)] =(D)u(t) +(D)v(t),

отсюда ошибка

(D)(t) =(D)u(t) +(D)v(t) -(D)r(t). (3.17)

Предположим, что:

1) имеют место нулевые начальные условия для ошибки и всех её производных

(t), ’(t),’’(t),...,^(n-1)= 0, n - степень;

2) многочлены ,,и значения г(t), v(t), t0 известны точно.

Тогда из (3.17) в соответствии с (3.15) можно определить инвариантное управление

(D)u(t) =(D)r(t) -(D)v(t) (3.18)

Подставляя управление (3.18) в (3.17) можно убедиться, что ошибка будет равна нулю

(D) (t) = 0. (3.19)

Идеальное управление особенно просто получить, если (D) =₀=const. В этом случае непосредственно из (3.18) следует управление

u(t) =₀^-1((D)r(t) -(D)v(t)) (3.20)