3. Методы анализа и синтеза управления.

3.1. Методы анализа управления (Лекция 10)

3.1.1. Управляемость, наблюдаемость.

3.1.1.1. Управляемость: определение (Пример 3.1)

Управляемость.Определение. Линейная дифференциальная система

(3.1)

является полностью управляемой тогда и только тогда, когда она может быть переведена из любого начального состояния в начальный момент временив любое конечное состояниеза конечное время-.

Теорема.n-мерная линейная система с постоянными параметрами

(3.2)

является полностью управляемой тогда и только тогда, когда вектор-столбец матрицы управляемости

(3.3)

порождает n-мерное пространство (имеет рангn).

Говорят пара {A,B} является полностью управляемой.

Пример 3.1. Проверить управляемость смесительного бака, модель которого получена в предыдущих примерах.

Если С=С, тоrangP=1 и система неуправляема; если СС, тоrangP=2 и система управляема.

3.1.1.2. Наблюдаемость: определение (Пример 3.2)

Наблюдаемость(восстанавливаемость) означает для системы (3.2), что по измерению выходной у(t) и входнойu(t),можно определить начальное состояние системыдля любого. Т.е. можно определить состояние в моментпо будущим управлениям или восстановить настоящее состояние по прошлым.

Теорема. Система (3.2)n-мерная является полностью восстановимой в том и только в том случае, если вектор-строка матрицы восстанавливаемостиQпорождаетn-мерное пространство(rangn)

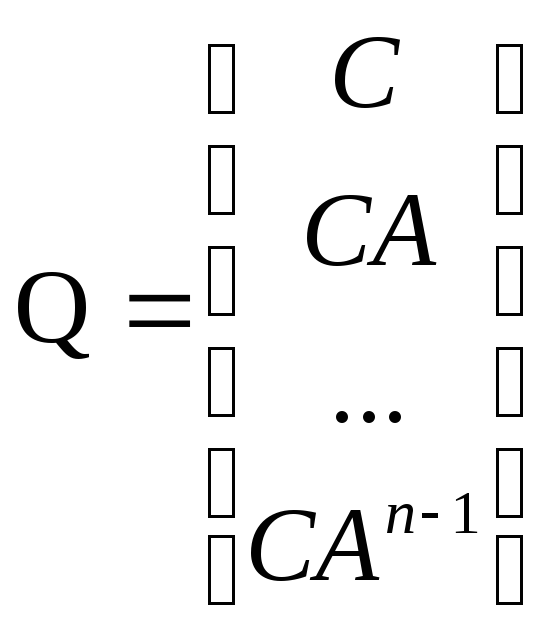(3.4)

Пример 3.2. Смесительный бак.

rangQ=2.

3.1.2. Корневой годограф

3.1.2.1. Определение корневого годографа

Анализ систем управления включает исследование устойчивости, качества, т.е. степени удовлетворения заданных характеристик качества, исследование динамической точности систем. Последнее особенно важно для следящих систем, в которых задающее воздействие - величина переменная во времени. Мы вкратце познакомимся с этими вопросами.

Основной принцип проектирования систем состоит в том, что система должна быть устойчивой.

Анализ устойчивости занимает исключительное положение. Кроме выяснения вопроса об устойчивости необходимо определить диапазоны варьирования параметров, в которых устойчивость сохраняется.

Чтобы быстро проследить поведение системы целесообразно использовать не точные вычисления, требующие много времени даже при использовании ЭВМ, а приближенные методы. Один из них метод корневого годографа.

Характеристическое уравнение замкнутой системы можно представить в виде

1 + H(р) = 1 + K (р)/(р) =(р) + K(р) = 0 (3.5)

Совокупность точек р_i, удовлетворяющих уравнению (3.5) при различных К, образует корневой годограф системы.

Таким образом, корневой годограф это геометрическое место точек – значений корней характеристического уравнения системы при изменении скалярного параметра от 0 до бесконечности. В качестве скалярного параметра часто выступает неизвестный вначале коэффициент усиления. Передаточная функция замкнутой системы для соединения с обратной связью, равна

H_з(p) =H_p(p) / [1 +H_p(p)H_oc(p)]

Её можно представить в виде (3.5)

(p) + (p) (3.6)

где ,- полиномы от, а- параметр. Полиномы можно представить в виде

(p) = _i (p - _i) , i=1,2,...,n; (p) = _i(p - _i), i=1,2,..,m (3.7)

где _i – обозначает произведение поi;_i , i=1,2,..,n - полюса разомкнутого контура, а_i, i=1,2,...,m - его нули.

Корни (3.6) называют полюсами замкнутого контура. Пусть m n, в обратном случае можно поменять местами,и выбрать параметр 1/.