
- •2. Некоторые методы анализа систем 10
- •1.1.1.2. Определение управления
- •1.1.1.3. Общие принципы системной организации
- •1.1.2. Общие принципы управления
- •1.1.2.5. Стохастическое управление
- •1.1.2.6. Нечеткое управление
- •1.1.2.7. Дискретное и непрерывное управление
- •1.2. Объекты, системы и их модели (Лекция 2)
- •1.2.1. Математические модели систем и объектов управления.
- •1.2.1.1. Математическая модель
- •1.2.1.2. Способы классификации моделей (объектов)
- •1.2.1.3. Некоторые виды математических моделей
- •1.2.2. Сложные системы
- •1.2.2.1. Примеры и свойства сложных систем
- •Кортежное описание сложных систем
- •1.2.2.3. Структура систем и объектов управления
- •1.2.2.4. Иерархия в системах управления.
- •1.2.2.5. Иерархия целей в системах управления.
- •1.2.2.6. Компромиссы и комплексные критерии
- •2. Некоторые методы анализа систем
- •2.1. Построение и упрощение моделей объекта (Лекция 3)
- •2.1.1. Упрощение моделей объекта
- •2.1.1.1. Замена нестационарной модели набором стационарных
- •2.1.1.2. Линеаризация модели
- •2.1.2. Пример построения модели объекта
- •2.1.2.1. Характеристика объекта
- •2.1.2.2. Разработка математической модели
- •Линеаризация
- •2.1.2.4. Линейная модель объекта
- •2.2. Временные характеристики систем управления (Лекция 4)
- •2.2.1. Линейные нестационарные системы
- •2.2.1.1. Общий вид описания системы
- •2.2.1.2. Решение однородного уравнения
- •2.2.1.3. Решение неоднородного уравнения
- •2.2.1.4. Фундаментальная матрица системы и её свойства
- •2.2.1.5. Весовая и переходная матрицы системы
- •2.2.2. Линейные стационарные системы
- •2.2.2.1. Фундаментальная матрица стационарной линейной системы
- •2.2.2.2. Весовая и переходная матрицы стационарной системы
- •2.3. Передаточная функция (Лекция 5)
- •2.3.1. Некоторые операторы
- •2.3.1.1. Дифференциальный оператор
- •2.3.1.2. Оператор Лапласа
- •2.3.2. Передаточная функция и резольвента
- •2.3.2.1. Фундаментальная матрица (резольвента)
- •2.3.2.2. Матричная передаточная функция
- •2.3.2.3.Простейший пример определения резольвенты (Пример п2.2)
- •2.3.2.4. Метод Фаддеевой (Сурье )определения резольвенты
- •2.3.2.5. Пример применения метода Фаддеевой (Пример 2.3)
- •2.4. Частотные характеристики (функции) систем (Лекция 6)
- •2.4.1. Частотная переходная функция
- •2.4.1.1. Напоминание о представлении комплексных чисел
- •2.4.1.2. Частотная передаточная функция
- •2.4.1.3. Смысл компонент матричной частотной функции (Пример2.4)
- •2.4.1.4. Виды используемых частотных характеристик
- •2.4.1.5. Пример вычисления характеристик (Пример2.5)
- •2.4.2. Логарифмические частотные характеристики
- •2.4.2.1. Смысл логарифмических частотных характеристик
- •2.4.2.2. Определение логарифмических частотных характеристик
- •2.4.2.3. Асимптотические логарифмические частотные характеристики
- •2.4.2.4. Иллюстрация построения асимптотических характеристик (Пример 2.6)
- •2.5. Структурные схемы систем (Лекция 7)
- •2.5.1. Схемы соединения звеньев
- •2.5.1.1. Представление звеньев и связей в виде структурных схем
- •2.5.1.2. Последовательное соединение звеньев
- •2.5.1.3. Параллельное соединение
- •2.5.1.4. Соединение с обратной связью
- •2.5.1.5. Пример определения матрицы возвратной разности (Пример 2.7)
- •2.5.2. Структурные преобразования линейных систем
- •2.5.2.1. Назначение и содержание структурных преобразований
- •2.5.2.2. Правила структурных преобразований линейных систем
- •2.5.2.3. Дополнительные правила для стационарных линейных систем
- •2.5.2.4. Иллюстративный пример (Пример2.8)
- •2.6. Анализ устойчивости систем управления (Лекция 8)
- •2.6.1. Определение устойчивости систем
- •2.6.1.1. Номинальное состояние и понятие устойчивости
- •2.6.1.2. Определения устойчивости решений
- •2.6.1.3. Устойчивость линейных дифференциальных систем
- •2.6.1.4. Пример смесительного бака (Пример2. 9)
- •2.6.2. Устойчивость линейных стационарных систем
- •2.6.2.1. Представление реакции системы с различными собственными числами
- •2.6.2.2. Представление реакции системы с кратными собственными числами
- •2.7.1.2. Необходимые условия
- •2.7.1.3. Достаточные условия
- •2.7.1.4. Пример применения алгоритма Раусса (Пример 2.11)
- •2.7.2. Частотные критерии
- •2.7.2.1. Нестрогое обоснование частотных критериев
- •2.7.2.2. Критерий Михайлова
- •2.7.2.3. Критерий Найквиста
- •3. Методы анализа и синтеза управления.
- •3.1. Методы анализа управления (Лекция 10)
- •3.1.1. Управляемость, наблюдаемость.
- •3.1.1.1. Управляемость: определение (Пример 3.1)
- •3.1.1.2. Наблюдаемость: определение (Пример 3.2)
- •3.1.2. Корневой годограф
- •3.1.2.1. Определение корневого годографа
- •3.1.2.2. Свойства корневого годографа
- •3.1.2.3. Пример построения корневого годографа (Пример 3.3)
- •3.2. Управление и стабилизация (Лекция 11)
- •3.2.1. Цель управления, идеальное управление
- •3.2.1.1. Общая схема разомкнутого и замкнутого управления
- •3.2.1.2. Идеальное управление
- •3.2.1.3. Пример определения идеального управления (Пример 3.4)
- •3.2.1.4. Невозможность реализации идеального управления
- •3.2.1.5. Иллюстрация недостатков идеального управления (Пример 3.5)
- •3.3. Стабилизация с помощью обратной связи (Лекция 12)
- •3.3.1. Введение обратной связи
- •3.3.1.1. Определение обратной связи в скалярном случае
- •3.3.1.2. Иллюстрация определения стабилизирующей обратной связи (Пример 3.6)
- •3.3.2. Общий алгоритм стабилизации
- •3.3.2.1. Общий вид обратной связи
- •3.3.2.2. Замкнутое представление объекта и обратной связи
- •3.3.2.3. Алгоритм выбора стабилизирующей обратной связи в общем случае
- •3.3.3. Некоторые другие законы управления
- •3.3.3.1. Программное управление в комбинации с обратной связью по выходу
- •3.3.3.2. Управление по возмущению
- •3.3.3.3. Управление с обратной связью по ошибке
- •3.4. Удовлетворение некоторых требований к качеству управления (Лекция 13)
- •3.4.1. Некоторые характеристики качества управления
- •3.4.1.1. Переходный процесс детерминированной системы и его некоторые характеристики
- •3.4.1.2. Некоторые требования к переходному процессу и установившейся ошибке
- •3.4.2. Методика удовлетворения требований к качеству
- •3.4.2.1. Теорема о реакции на полиномиальное воздействие
- •3.4.2.2. Обеспечение требования ограниченности установившейся ошибки
- •3.4.2.3. Обеспечение ограниченности амплитуды ошибки при периодическом воздействии
- •3.4.2.4. Обеспечение ограниченности амплитуды ошибки при периодической помехе
- •4. Цифровые системы управления.
- •4.1. Модели, формула полной реакции, устойчивость. (Лекция 14)
- •4.1.1. Модели
- •4.1.1.1. Кусочно-постоянный процесс
- •4.1.1.2. Описание дискретных систем
- •4.1.1.3. Пример дискретной системы (Пример 4.1)
- •4.1.1.1. Дискретизация непрерывной модели
- •4.1.2. Решение разностных уравнений
- •4.1.2.1. Переходная матрица
- •4.1.2.2. Матричная импульсная переходная функция
- •4.1.2.3. Устойчивость
- •4.2. Синтез оптимального линейного дискретного регулятора (Лекция 15)
- •4.2.1. Методика синтеза оптимального управления
- •4.2.1.1. Многошаговое управление
- •4.2.1.2. Критерий оптимальности
- •4.2.1.3. Принцип оптимальности Беллмана
- •4.2.2. Синтез одношагового оптимального управления
- •4.2.2.1. Формирование критерия для одношаговой задачи
- •4.2.2.2. Определение вектора оптимального управления
- •4.2.2.3. Принцип перехода к многошаговой задаче
- •5. Стохастические системы
- •5.1. Стохастические процессы (Лекция 16)
- •5.1.1. Определение и естественные характеристики случайного процесса
- •5.1.1.1. Определение случайного процесса
- •5.1.1.2. Характеристики случайного процесса
- •5.1.2. Спектральное представление случайного процесса
- •5.1.2.1. Спектр функции
- •5.1.2.2. Спектральная плотность
- •5.1.2.3. Физический смысл гармонического анализа случайного процесса
- •5.1.2.4. Взаимосвязь функций времени и их спектрального представления
- •5.1.2.5. Матрица спектральных плотностей энергии
- •5.1.2.6. Пример определения функции спектральной плотности по ковариационной функции (Пример 5.1)
- •5.2. Задачи слежения (Лекция 17)
- •5.2.1. Характеристики качества следящих систем.
- •5.2.1.1. Описание разомкнутой следящей системы
- •5.2.1.2. Описание замкнутой следящей системы.
- •5.2.1.2. Интегральные характеристики качества регулирования
- •5.2.1.3. Среднее значение и дисперсия характеристик качества регулирования
- •5.2.1.4. Передаточные функции замкнутой системы
- •5.2.2. Примеры анализа стохастических систем
- •5.2.2.1. Реакция линейной системы стохастические внешние воздействия
- •5.2.2.2. Реакция линейных дифференциальных систем на белый шум
- •5.2.2.3. Пример дифференциальной системы, возбуждаемой белым шумом(Пример 5.2)
- •5.2.2.4. Моделирование стохастических процессов.
- •5.2.2.5. Моделирование стационарного процесса уравнением 1-го порядка (Пример 5.3)
- •5.2.3. Некоторые принципы проектирования следящих систем.
- •5.2.3.1. Устойчивость
- •5.2.3.2. Требования к следящей системе
- •5.2.3.3. Соглашение о входных воздействиях
- •5.2.4. Использование полос пропускания при проектировании
- •5.2.4.1. Скалярный случай
- •5.2.4.2. Принцип проектирования
- •5.2.4.3. Полоса частот системы
- •5.2.4.4. Полоса частот эталонного процесса
- •5.2.4.5. Реализация принципа проектирования( минимизация ошибки)
- •5.2.4.6. Реализация принципа проектирования ( минимизация входной переменной)
- •5.2.4.7. Оценка длительности переходных процессов
- •6. Адаптивные системы
- •6.1. Адаптивные системы и идентификация (Лекция 17)
- •6.1.1. Основные схемы адаптивных систем
- •6.1.1.1. Предназначение адаптации
- •6.1.1.2. Схема адаптации по разомкнутому контуру
- •6.1.1.3. Схема с самонастраивающимся регулятором
- •6.1.1.4. Схема с настройкой регулятора по эталонной модели
- •6.1.1.5. Общая схема адаптивной системы
- •6.1.2. Идентификация моделей
- •6.1.2.1. Идентификация структурная и параметрическая
- •6.1.2.2. Содержание метода наименьших квадратов
- •6.1.2.3. Рекуррентный алгоритм метода наименьших квадратов
4.1.2. Решение разностных уравнений
4.1.2.1. Переходная матрица
Системы, описываемые разностными уравнениями, имеют характеристики, подобные характеристикам, рассмотренным в разделе 3 для непрерывных систем. Для их получения и анализа привлекаются соответствующие математические методы. Например, для получения передаточных функций применяется дискретное или Z – преобразование Лапласа. Эти вопросы могут быть изучены по литературе, список которой приложен к лекциям. Здесь вкратце рассматриваются переходные характеристики, которые для дискретных систем имеют достаточно простой вид и вычисление которых ориентировано на ЦВМ.
В качестве первой характеристики рассмотрим переходную матрицу.
Теорема 1.Рассмотрим разностное уравнение состояния
x(i+1) =A(i)x(i) +B(i)u(i). (4.10)
Решение его может быть представлено в виде
x(i)
=Ф(i,i0)x(i0)
+
![]() Ф(i,j+1)B(j)u(j),i i0+ 1,
(4.11)
Ф(i,j+1)B(j)u(j),i i0+ 1,
(4.11)
где Ф(i,i0),ii0 естьпереходная матрица, определяемая так:
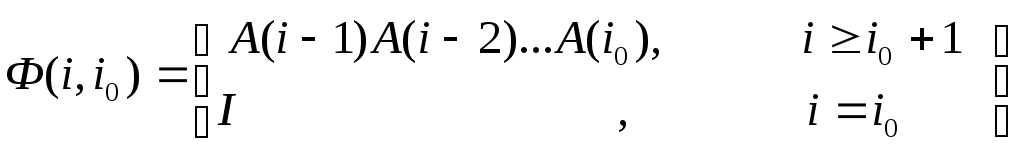 .
(4.12)
.
(4.12)
Переходная матрица Ф(i,i0) является решением матричного уравнения
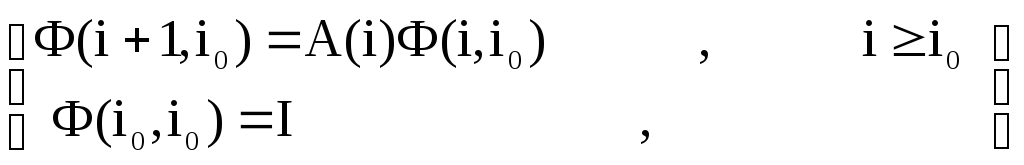 .
(4.13)
.
(4.13)
Если
система стационарная А(i)
=A
![]() i, то переходная матрица
представляет соответствующую степень
матрицыA:
i, то переходная матрица
представляет соответствующую степень
матрицыA:
Ф(i,i0) =Ai - i0(4.14)
Формулы (4.11) и (4.12) могут быть получены непосредственно по модели (4.10), если в ней выражать х(i) черезx(i-1),x(i-1) - черезx(i-2) и так далее доx(i0).
4.1.2.2. Матричная импульсная переходная функция
Выходная переменная описывается уравнением (4.9), пусть x(i0) = 0. Подставив (4.11) в (4.9), получим следующую зависимость для выходной переменнойy(i):
y(i)
=
![]() K(i,j)
u(j),
i
i0
, (4.15)
K(i,j)
u(j),
i
i0
, (4.15)
где
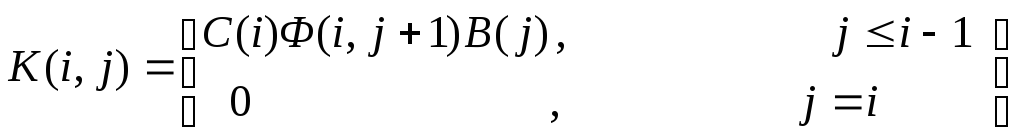 .
(4.16)
.
(4.16)
Выражение (4.16) представляет собой матричную импульсную переходную функцию системы. ЕслиАпостоянная матрица, тоК(i,j) =К(i-j).
Если система имеет прямую связь, т.е. управляющая величина воздействует непосредственно на выходную переменную, и выходная переменная описывается следующим образом:
y(i) = C(i)x(i) + D(i)u(i) (4.17),
то вместо нуля в матричной импульсной переходной функции (4.16) появится матрица D(i):
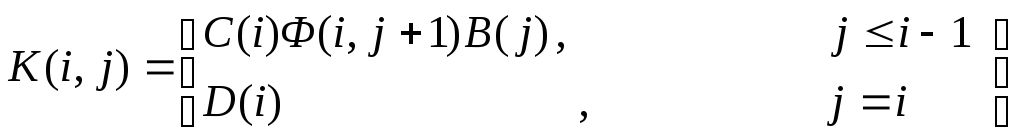 (4.18)
(4.18)
4.1.2.3. Устойчивость
Ограничиваясь системами с постоянными параметрами, нетрудно видеть, что переходная матрица выражается через степени матрицы А. МатрицуАможно привести к диагональному виду, когда на главной диагонали будут стоять корни характеристического уравненияi, а все остальные элементы будут равны нулю.
Степени матрицы Авыразятся через соответствующие степени её собственных чисел (корни). Таким образом, решение можно представить в виде композиции расходящихся при |i|1, установившихся при |i| = 1 и сходящихся при |i|1 движений по собственным векторам.
На дискретные системы можно перенести всё сказанное для непрерывных систем, заменив условие отрицательности действительных частей корней в случае непрерывных систем, условием |i|1 для дискретных систем.
Например, линейная дискретная система с постоянными параметрами
x(i+1) =Ax(i) асимптотически устойчива в том и только в том случае, если все характеристические числа матрицыАпо модулю строго меньше единицы.
