3.4.2.2. Обеспечение требования ограниченности установившейся ошибки

Применяя теорему к условию 2) из п. 3.4.1.2, получим для установившейся ошибки

 _ (t) = r(t) - y _ (t) = [1 - H_з (0)] (a₀ + a₁t) + [d(1 - H_з (p)) / dp]_p=0 a₁ (3.59)

Отсюда видно, что ошибка может быть ограничена при а₁0 только в случае выполнения условия астатизма

Н_з (0) = 1; (3.60)

т.к. Н_з(р) = Н_р(р) [ 1 + Н_р(з) ]^-1,

то для выполнения (3.60) должно быть Н_р^{- 1}(0) = 0. Чтобы убедиться в этом, достаточно умножить числитель и знаменатель правой части последнего выражения на Н_р^{- 1}(0):

(Н_р(0) Н_р^{- 1}(0)) [1 H_p^{- 1}(0) + H_p(0) H_p^{- 1}(0) ]^{- 1}= 1.

Это возможно только, если разомкнутая передаточная функция имеет нулевой полюс, т.е. в знаменателе члены вида (р - 0) = р. Если этот полюс простой, то передаточную функцию разомкнутой системы можно представить в виде:

Н_р(р) = k_p H1_p(p) / p, H1_p(0) =1, k_p = const , (3.61)

тогда d/dp[1-H_з(p)]_p=0 = d/dp[p/ (p + k_pH1_p(p))]_p=0 = k_p^{- 1}

и, следовательно, из (3.59) получим

 _=a₁ k_p^{- 1}=const.

Таким образом для выполнения требования 2) из п. 3.4.1.2 можно принять разомкнутую передаточную функцию в виде (3.61), причем коэффициент k_рдолжен удовлетворять условию

, (3.62)

где ₀^{- 1}- называется добротностью системы.

3.4.2.3. Обеспечение ограниченности амплитуды ошибки при периодическом воздействии

Теперь обратимся к требованию 3) из п. 3.4.1.2. Известно, что реакция линейной дифференциальной системы на гармоническое воздействие является гармонической функцией с амплитудой

a _= | 1 - H _з(j)| a_r .

Следовательно, для удовлетворения требования (3.53) необходимо, чтобы желаемая передаточная функция замкнутой системы подчинялась ограничению

| 1 - H_з(j)|= _r, _r , (3.63)

что эквивалентно ограничению на разомкнутую передаточную функцию.

| 1 + H_p(j) | _r ^{- 1}, _r . (3.64)

3.4.2.4. Обеспечение ограниченности амплитуды ошибки при периодической помехе

Требование 4) п. 3.4.1.2 также учитывается через ограничения на передаточную функцию системы в виде

| H_з(j) |= _N , _N(3.65)

или через разомкнутую передаточную функцию

| 1 + H_p(j) | _N^{- 1} ,_N. (3.66)

Все требования обеспечиваются выбором передаточной функции замкнутой системы. Если передаточная функция объекта не удовлетворяет сформулированным требованиям, то при разработке регулятора вводятся обратные связи, обеспечивающие удовлетворение этих требований через замкнутую передаточную функцию.

Ещё раз подчеркнём, что требования к качественным показателям системы обеспечиваются расположением корней характеристического уравнения замкнутой системы. Требования к качеству в общем противоречивы. Задача проектировщика состоит в поиске рациональной альтернативы различных требований, в их упорядочивании и, в конечном итоге, обеспечении наилучшего сочетания показателей качества системы.

4. Цифровые системы управления.

4.1. Модели, формула полной реакции, устойчивость. (Лекция 14)

4.1.1. Модели

4.1.1.1. Кусочно-постоянный процесс

Обратимся теперь к дискретным системам, которые описываются моделями вида (1.6), (1.8). В них используются кусочно-постоянные сигналы и функции. Такие функции могут возникать естественным образом или получаться в результате дискретизации непрерывных величин.

Например, состояния счетов в банке описываются кусочно-постоянными функциями, которые изменяют свои значения только в моменты перечисления средств.

При управлении непрерывным объектом с помощью дискретного контроллера сигналы с объекта на контроллер подаются через аналогово-цифровой преобразователь и дискретизируются. Дискретные управляющие величины, вычисляемые контроллером, преобразуются цифро-аналоговым преобразователем и подаются на аналоговые исполнительные устройства объекта.

На рис. 4.1 показан график кусочно-постоянного процесса, в котором значения z(t) изменяются на правых границах интервалов времени.

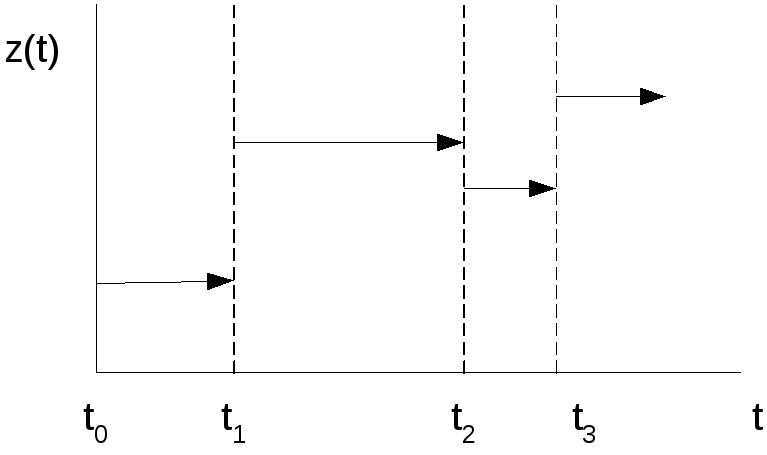
Рис. 4.1. Кусочно-постоянный процесс.

Формально такой график описывается так: z(t) = z(t_i)t[t_i, t_i+1). Правая граница в интервал не включается, на ней значение функции изменяется скачком от z(t_i) до z(t_i+1). Интервалыt_i = t _i+1 - t _i,i= 0, 1, …. не обязательно должны быть равными, но для удобства и простоты часто их принимают постояннымиt_i=ti = 0, 1, ..., тогдаt_i=t₀+itили приt₀=0t_i=it.

Моменты времени нумеруются t _i+1= t_i+t_i, i = 0, 1, ... и, учитывая однозначное соответствие t_ii, номер момента может быть использован в качестве дискретного времениz(t_i) =z(i).