
- •2. Некоторые методы анализа систем 10
- •1.1.1.2. Определение управления
- •1.1.1.3. Общие принципы системной организации
- •1.1.2. Общие принципы управления
- •1.1.2.5. Стохастическое управление
- •1.1.2.6. Нечеткое управление
- •1.1.2.7. Дискретное и непрерывное управление
- •1.2. Объекты, системы и их модели (Лекция 2)
- •1.2.1. Математические модели систем и объектов управления.
- •1.2.1.1. Математическая модель
- •1.2.1.2. Способы классификации моделей (объектов)
- •1.2.1.3. Некоторые виды математических моделей
- •1.2.2. Сложные системы
- •1.2.2.1. Примеры и свойства сложных систем
- •Кортежное описание сложных систем
- •1.2.2.3. Структура систем и объектов управления
- •1.2.2.4. Иерархия в системах управления.
- •1.2.2.5. Иерархия целей в системах управления.
- •1.2.2.6. Компромиссы и комплексные критерии
- •2. Некоторые методы анализа систем
- •2.1. Построение и упрощение моделей объекта (Лекция 3)
- •2.1.1. Упрощение моделей объекта
- •2.1.1.1. Замена нестационарной модели набором стационарных
- •2.1.1.2. Линеаризация модели
- •2.1.2. Пример построения модели объекта
- •2.1.2.1. Характеристика объекта
- •2.1.2.2. Разработка математической модели
- •Линеаризация
- •2.1.2.4. Линейная модель объекта
- •2.2. Временные характеристики систем управления (Лекция 4)
- •2.2.1. Линейные нестационарные системы
- •2.2.1.1. Общий вид описания системы
- •2.2.1.2. Решение однородного уравнения
- •2.2.1.3. Решение неоднородного уравнения
- •2.2.1.4. Фундаментальная матрица системы и её свойства
- •2.2.1.5. Весовая и переходная матрицы системы
- •2.2.2. Линейные стационарные системы
- •2.2.2.1. Фундаментальная матрица стационарной линейной системы
- •2.2.2.2. Весовая и переходная матрицы стационарной системы
- •2.3. Передаточная функция (Лекция 5)
- •2.3.1. Некоторые операторы
- •2.3.1.1. Дифференциальный оператор
- •2.3.1.2. Оператор Лапласа
- •2.3.2. Передаточная функция и резольвента
- •2.3.2.1. Фундаментальная матрица (резольвента)
- •2.3.2.2. Матричная передаточная функция
- •2.3.2.3.Простейший пример определения резольвенты (Пример п2.2)
- •2.3.2.4. Метод Фаддеевой (Сурье )определения резольвенты
- •2.3.2.5. Пример применения метода Фаддеевой (Пример 2.3)
- •2.4. Частотные характеристики (функции) систем (Лекция 6)
- •2.4.1. Частотная переходная функция
- •2.4.1.1. Напоминание о представлении комплексных чисел
- •2.4.1.2. Частотная передаточная функция
- •2.4.1.3. Смысл компонент матричной частотной функции (Пример2.4)
- •2.4.1.4. Виды используемых частотных характеристик
- •2.4.1.5. Пример вычисления характеристик (Пример2.5)
- •2.4.2. Логарифмические частотные характеристики
- •2.4.2.1. Смысл логарифмических частотных характеристик
- •2.4.2.2. Определение логарифмических частотных характеристик
- •2.4.2.3. Асимптотические логарифмические частотные характеристики
- •2.4.2.4. Иллюстрация построения асимптотических характеристик (Пример 2.6)
- •2.5. Структурные схемы систем (Лекция 7)
- •2.5.1. Схемы соединения звеньев
- •2.5.1.1. Представление звеньев и связей в виде структурных схем
- •2.5.1.2. Последовательное соединение звеньев
- •2.5.1.3. Параллельное соединение
- •2.5.1.4. Соединение с обратной связью
- •2.5.1.5. Пример определения матрицы возвратной разности (Пример 2.7)
- •2.5.2. Структурные преобразования линейных систем
- •2.5.2.1. Назначение и содержание структурных преобразований
- •2.5.2.2. Правила структурных преобразований линейных систем
- •2.5.2.3. Дополнительные правила для стационарных линейных систем
- •2.5.2.4. Иллюстративный пример (Пример2.8)
- •2.6. Анализ устойчивости систем управления (Лекция 8)
- •2.6.1. Определение устойчивости систем
- •2.6.1.1. Номинальное состояние и понятие устойчивости
- •2.6.1.2. Определения устойчивости решений
- •2.6.1.3. Устойчивость линейных дифференциальных систем
- •2.6.1.4. Пример смесительного бака (Пример2. 9)
- •2.6.2. Устойчивость линейных стационарных систем
- •2.6.2.1. Представление реакции системы с различными собственными числами
- •2.6.2.2. Представление реакции системы с кратными собственными числами
- •2.7.1.2. Необходимые условия
- •2.7.1.3. Достаточные условия
- •2.7.1.4. Пример применения алгоритма Раусса (Пример 2.11)
- •2.7.2. Частотные критерии
- •2.7.2.1. Нестрогое обоснование частотных критериев
- •2.7.2.2. Критерий Михайлова
- •2.7.2.3. Критерий Найквиста
- •3. Методы анализа и синтеза управления.
- •3.1. Методы анализа управления (Лекция 10)
- •3.1.1. Управляемость, наблюдаемость.
- •3.1.1.1. Управляемость: определение (Пример 3.1)
- •3.1.1.2. Наблюдаемость: определение (Пример 3.2)
- •3.1.2. Корневой годограф
- •3.1.2.1. Определение корневого годографа
- •3.1.2.2. Свойства корневого годографа
- •3.1.2.3. Пример построения корневого годографа (Пример 3.3)
- •3.2. Управление и стабилизация (Лекция 11)
- •3.2.1. Цель управления, идеальное управление
- •3.2.1.1. Общая схема разомкнутого и замкнутого управления
- •3.2.1.2. Идеальное управление
- •3.2.1.3. Пример определения идеального управления (Пример 3.4)
- •3.2.1.4. Невозможность реализации идеального управления
- •3.2.1.5. Иллюстрация недостатков идеального управления (Пример 3.5)
- •3.3. Стабилизация с помощью обратной связи (Лекция 12)
- •3.3.1. Введение обратной связи
- •3.3.1.1. Определение обратной связи в скалярном случае
- •3.3.1.2. Иллюстрация определения стабилизирующей обратной связи (Пример 3.6)
- •3.3.2. Общий алгоритм стабилизации
- •3.3.2.1. Общий вид обратной связи
- •3.3.2.2. Замкнутое представление объекта и обратной связи
- •3.3.2.3. Алгоритм выбора стабилизирующей обратной связи в общем случае
- •3.3.3. Некоторые другие законы управления
- •3.3.3.1. Программное управление в комбинации с обратной связью по выходу
- •3.3.3.2. Управление по возмущению
- •3.3.3.3. Управление с обратной связью по ошибке
- •3.4. Удовлетворение некоторых требований к качеству управления (Лекция 13)
- •3.4.1. Некоторые характеристики качества управления
- •3.4.1.1. Переходный процесс детерминированной системы и его некоторые характеристики
- •3.4.1.2. Некоторые требования к переходному процессу и установившейся ошибке
- •3.4.2. Методика удовлетворения требований к качеству
- •3.4.2.1. Теорема о реакции на полиномиальное воздействие
- •3.4.2.2. Обеспечение требования ограниченности установившейся ошибки
- •3.4.2.3. Обеспечение ограниченности амплитуды ошибки при периодическом воздействии
- •3.4.2.4. Обеспечение ограниченности амплитуды ошибки при периодической помехе
- •4. Цифровые системы управления.
- •4.1. Модели, формула полной реакции, устойчивость. (Лекция 14)
- •4.1.1. Модели
- •4.1.1.1. Кусочно-постоянный процесс
- •4.1.1.2. Описание дискретных систем
- •4.1.1.3. Пример дискретной системы (Пример 4.1)
- •4.1.1.1. Дискретизация непрерывной модели
- •4.1.2. Решение разностных уравнений
- •4.1.2.1. Переходная матрица
- •4.1.2.2. Матричная импульсная переходная функция
- •4.1.2.3. Устойчивость
- •4.2. Синтез оптимального линейного дискретного регулятора (Лекция 15)
- •4.2.1. Методика синтеза оптимального управления
- •4.2.1.1. Многошаговое управление
- •4.2.1.2. Критерий оптимальности
- •4.2.1.3. Принцип оптимальности Беллмана
- •4.2.2. Синтез одношагового оптимального управления
- •4.2.2.1. Формирование критерия для одношаговой задачи
- •4.2.2.2. Определение вектора оптимального управления
- •4.2.2.3. Принцип перехода к многошаговой задаче
- •5. Стохастические системы
- •5.1. Стохастические процессы (Лекция 16)
- •5.1.1. Определение и естественные характеристики случайного процесса
- •5.1.1.1. Определение случайного процесса
- •5.1.1.2. Характеристики случайного процесса
- •5.1.2. Спектральное представление случайного процесса
- •5.1.2.1. Спектр функции
- •5.1.2.2. Спектральная плотность
- •5.1.2.3. Физический смысл гармонического анализа случайного процесса
- •5.1.2.4. Взаимосвязь функций времени и их спектрального представления
- •5.1.2.5. Матрица спектральных плотностей энергии
- •5.1.2.6. Пример определения функции спектральной плотности по ковариационной функции (Пример 5.1)
- •5.2. Задачи слежения (Лекция 17)
- •5.2.1. Характеристики качества следящих систем.
- •5.2.1.1. Описание разомкнутой следящей системы
- •5.2.1.2. Описание замкнутой следящей системы.
- •5.2.1.2. Интегральные характеристики качества регулирования
- •5.2.1.3. Среднее значение и дисперсия характеристик качества регулирования
- •5.2.1.4. Передаточные функции замкнутой системы
- •5.2.2. Примеры анализа стохастических систем
- •5.2.2.1. Реакция линейной системы стохастические внешние воздействия
- •5.2.2.2. Реакция линейных дифференциальных систем на белый шум
- •5.2.2.3. Пример дифференциальной системы, возбуждаемой белым шумом(Пример 5.2)
- •5.2.2.4. Моделирование стохастических процессов.
- •5.2.2.5. Моделирование стационарного процесса уравнением 1-го порядка (Пример 5.3)
- •5.2.3. Некоторые принципы проектирования следящих систем.
- •5.2.3.1. Устойчивость
- •5.2.3.2. Требования к следящей системе
- •5.2.3.3. Соглашение о входных воздействиях
- •5.2.4. Использование полос пропускания при проектировании
- •5.2.4.1. Скалярный случай
- •5.2.4.2. Принцип проектирования
- •5.2.4.3. Полоса частот системы
- •5.2.4.4. Полоса частот эталонного процесса
- •5.2.4.5. Реализация принципа проектирования( минимизация ошибки)
- •5.2.4.6. Реализация принципа проектирования ( минимизация входной переменной)
- •5.2.4.7. Оценка длительности переходных процессов
- •6. Адаптивные системы
- •6.1. Адаптивные системы и идентификация (Лекция 17)
- •6.1.1. Основные схемы адаптивных систем
- •6.1.1.1. Предназначение адаптации
- •6.1.1.2. Схема адаптации по разомкнутому контуру
- •6.1.1.3. Схема с самонастраивающимся регулятором
- •6.1.1.4. Схема с настройкой регулятора по эталонной модели
- •6.1.1.5. Общая схема адаптивной системы
- •6.1.2. Идентификация моделей
- •6.1.2.1. Идентификация структурная и параметрическая
- •6.1.2.2. Содержание метода наименьших квадратов
- •6.1.2.3. Рекуррентный алгоритм метода наименьших квадратов
2.3.2.3.Простейший пример определения резольвенты (Пример п2.2)
![]() Пример П2.2. Для
условий примера П2.1 - смесительный бак
было найдено матрично-векторное уравнение
для состояний (П1.12) и выходных величин
(П1.15) в виде:
Пример П2.2. Для
условий примера П2.1 - смесительный бак
было найдено матрично-векторное уравнение
для состояний (П1.12) и выходных величин
(П1.15) в виде:
 ,
(П2.1)
,
(П2.1)
 .
(П2.2)
.
(П2.2)
Вследствие простоты здесь резольвента может быть вычислена непосредственно по формуле Ф(p) = (pI - A)-1. Действительно,
(pI
- A)
=
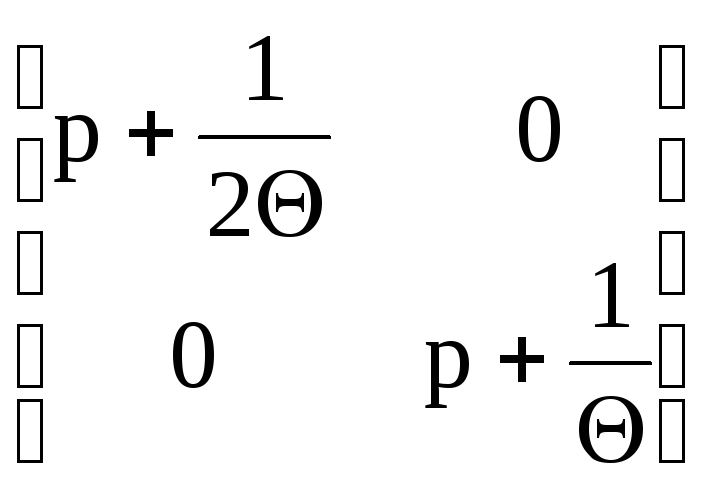 ,
adj (pI
- A)
=
,
adj (pI
- A)
= ,
,
Ф(р)
=
(pI
- A)-1
=
 .(П2.3)
.(П2.3)
Передаточная матрица определяется по резольвенте и матрицам из (П2.1) и (П2.2) в виде
![]() .
.
Выполнив перемножения матриц, получим матричную передаточную функцию
H(p)
 .
(П2.4)
.
(П2.4)
Если подставить численные значения, то получим
 ,
,
![]() .
(П2.5)
.
(П2.5)![]()
2.3.2.4. Метод Фаддеевой (Сурье )определения резольвенты
Резольвенты для систем большой размерности можно определять следуя разработанным для этой цели алгоритмам. Один из них состоит в следующем. Пусть А - n´n матрица с постоянными параметрами, имеющая характеристический полином det(pI-A) = pn + an-1 pn-1 + ... + a1p + a0. Её резольвента Ф(p) может быть записана в виде
![]() ,
(a)
,
(a)
где
![]() ,i=1,2…n,
,i=1,2…n,
![]()
Для определения Ri, i = 1,2,....,n может быть использован следующий алгоритм.
Пусть
an = 1 , Rn = 1,
тогда
![]() .
(б)
.
(б)
Здесь![]() -
след матрицыМ.
-
след матрицыМ.
Rn-k = an-kI + AR n-k+1, k = 1, 2, ,...., n, (в)
при k = n должно быть R0 = 0.
Это метод Сурье или Фаддеевой, который следует из алгоритма Леверье.
Условие R0 = 0 может быть использовано для проверки. Существуют и другие методы. Например, следствие из теоремы Кели-Гамильтона (каждая квадратная матрица удовлетворяет своему характеристическому уравнению) и др.
2.3.2.5. Пример применения метода Фаддеевой (Пример 2.3)
![]() Пример
П2.3: дана
система
Пример
П2.3: дана
система

Найти Ф(p).
Решение:
Способ №1 (непосредственное вычисление).
![]() ,
т.к.
,
т.к.
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,![]()
 ;
;
Способ №2 (метод Сурье).
n=2,
k=1,
α2![]()
![]() ,
,
α1 ,
,
![]() .
.
α0 ,
,
![]() .
.
 .
.![]()
2.4. Частотные характеристики (функции) систем (Лекция 6)
2.4.1. Частотная переходная функция
2.4.1.1. Напоминание о представлении комплексных чисел
Частотные характеристики характеризуют зависимость реакции системы от частоты периодического входного воздействия. Зависимость от частоты может характеризоваться изменением амплитуды и фазы входного сигнала. Для представления этих двух важнейших характеристик удобно использовать комплексные числа, которые, как известно, содержат в себе обе эти характеристики.
Поэтому вспомним формы представления комплексных чисел и используемые при этом термины. Из курса математики известно, что любое комплексное число имеет вид:
z = a + jb,
где a=Re z – его действительная часть (от латинского Realis -действительный),
b=Im z – его мнимая часть (от латинского Imaginarias - мнимый).
На комплексной плоскости комплексное число представляется в виде, показанном на рис. 2.2, где a и b – действительная и мнимая части числа, A – его модуль, а φ – аргумент.

Рис. 2.2. Представление числа на комплексной плоскости
Комплексное число можно представить также в показательной и тригонометрической форме:
z = A(z)ejarg z = A(z) (cos j + j sin j),
где
A(z)
=
![]() - модуль комплексного числа, который в
теории управления называется
- модуль комплексного числа, который в
теории управления называется
амплитудой;
arg z = arctg b/a = φ – аргумент, который в теории управления называется фазой.
Выражения тригонометрических функций через показательные можно получить с помощью формул Эйлера:
cos φ = (ejφ + e- jφ) /2, sin φ = (ejφ - e- jφ) /2j.
