2.4. Плоскость в пространстве.

  ЗАДАНИЕ N 6 сообщить об ошибке Тема: Плоскость в пространстве Уравнение плоскости, проходящей через точки   и   параллельно вектору   имеет вид …

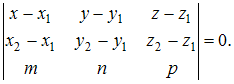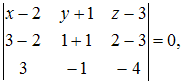Решение: Рассмотрим некоторую точку   принадлежащую искомой плоскости. Необходимо, чтобы вектора     и   были компланарны. То есть уравнение плоскости, проходящей через точки    и    параллельно вектору  , может быть представлено в следующем виде:  Тогда   или 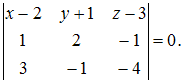 Следовательно, уравнение плоскости примет вид:

  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Плоскость в пространстве Уравнение плоскости, проходящей через точку   параллельно векторам   и   имеет вид …

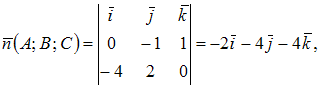Решение: Уравнение плоскости, проходящей через точку   с нормальным вектором   имеет вид:   В качестве нормального вектора плоскости возьмем векторное произведение векторов   и  Тогда   или  Подставляя в уравнение плоскости координаты точки   и вектора   получим:   или 

  ЗАДАНИЕ N 18 сообщить об ошибке Тема: Плоскость в пространстве Плоскости   и   перпендикулярны при значении m, равном …

Решение: Плоскости, заданные общими уравнениями   и   перпендикулярны при условии, что   Тогда    то есть 

  ЗАДАНИЕ N 22 сообщить об ошибке Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку   параллельно плоскости   имеет вид …

Решение: Уравнение плоскости, параллельной плоскости   имеет вид:   Подставим координаты точки   в это уравнение:   Тогда 

  ЗАДАНИЕ N 28 сообщить об ошибке Тема: Плоскость в пространстве Уравнение плоскости, проходящей через точку   перпендикулярно плоскостям   и   имеет вид …

Решение: Уравнение плоскости, проходящей через точку   с нормальным вектором   имеет вид:   В качестве нормального вектора плоскости возьмем векторное произведение нормальных векторов плоскостей   и   Тогда 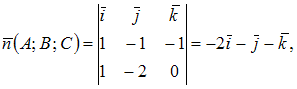  или   Подставляя в уравнение плоскости координаты точки   и вектора   получим:   или 

  ЗАДАНИЕ N 18 сообщить об ошибке Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку   и отсекающей равные отрезки на координатных осях, имеет вид …

Решение: Уравнение плоскости «в отрезках» имеет вид   где   – длины отрезков, отсекаемых плоскостью на осях Ox, Oy и Oz соответственно. Так как отрезки равны, то   или   Подставим в это уравнение координаты точки     то есть   Тогда уравнение плоскости примет вид   или 

  ЗАДАНИЕ N 27 сообщить об ошибке Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку   перпендикулярно прямой   имеет вид …

Решение: Уравнение плоскости, проходящей через точку   с нормальным вектором   имеет вид:  Так как эта плоскость перпендикулярна прямой   то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть   Тогда  или 

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Плоскость в пространстве Даны три пары плоскостей: 1)   и  2)   и  3)   и  Тогда …

			перпендикулярна первая пара плоскостей
			перпендикулярна вторая пара плоскостей
			перпендикулярна третья пара плоскостей
			среди заданных пар плоскостей перпендикулярных пар нет

Решение: Условие перпендикулярности двух плоскостей, заданных уравнениями   и  , имеет вид  . Условию перпендикулярности удовлетворяют плоскости   и  , то есть перпендикулярна первая пара плоскостей.

  ЗАДАНИЕ N 24 сообщить об ошибке Тема: Плоскость в пространстве Угол между плоскостями   и   равен …

			0

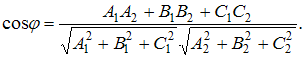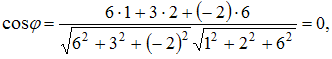Решение: Угол, образованный двумя плоскостями   и   определяется из соотношения   Тогда   или 

  ЗАДАНИЕ N 23 сообщить об ошибке Тема: Плоскость в пространстве Уравнение плоскости, проходящей через точки     и   имеет вид …

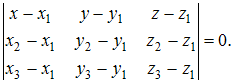Решение: Уравнение плоскости, проходящей через точки     и   не лежащие на одной прямой, имеет вид  Подставим числовые значения в полученное уравнение: 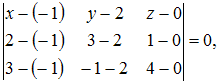 или 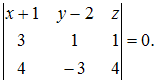  Раскрывая определитель по первой строке, получим  то есть 

ДЕ 3. Дифференциальное и интегральное исчисление

3.1. Область определения функции

3.2. Непрерывность функции, точки разрыва

3.3. Производные высших порядков

3.4. Дифференциальное исчисление ФНП

3.5. Основные методы интегрирования

3.6. Свойства определенного интеграла