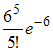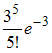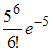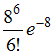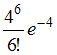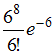- •Структура теста
- •1.1. Вычисление определителей.
- •1.2. Умножение матриц.
- •1.3. Определение линейного пространства.
- •1.4. Квадратичные формы.
- •2.1. Полярные координаты на плоскости.
- •2.2. Прямая на плоскости.
- •2.3. Кривые второго порядка.
- •2.4. Плоскость в пространстве.
- •3.1. Область определения функции.
- •3.2. Непрерывность функции, точки разрыва.
- •3.3. Производные высших порядков.
- •3.4. Дифференциальное исчисление фнп.
- •3.5. Основные методы интегрирования.
- •3.6. Свойства определенного интеграла.
- •4.1. Числовые последовательности.
- •4.2. Сходимость числовых рядов.
- •4.3. Область сходимости степенного ряда.
- •4.4. Ряд Тейлора (Маклорена).
- •5.1. Типы дифференциальных уравнений.
- •5.2. Однородные дифференциальные уравнения.
- •5.3. Задача Коши для дифференциального уравнения первого порядка.
- •5.4. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •6.1. Определение вероятности.
- •6.2. Теоремы сложения и умножения вероятностей.
- •6.3. Законы распределения вероятностей дискретных случайных величин
- •6.4. Числовые характеристики случайных величин
- •7.1. Характеристики вариационного ряда.
- •7.2. Интервальные оценки параметров распределения.
- •7.3. Элементы корреляционного анализа.
- •7.4. Проверка статистических гипотез.
- •8.1. Линейное программирование: аналитическое задание области допустимых решений.
- •8.2. Транспортная задача.
- •8.3. Теория игр: матричные игры.
- •8.4. Сетевое планирование и управление.
- •9.1. Функция полезности.
- •9.2. Производственные функции.
- •9.3. Коэффициенты эластичности.
- •9.4. Статическая модель межотраслевого баланса.
6.3. Законы распределения вероятностей дискретных случайных величин
ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина X задана
законом распределения вероятностей:
 Тогда
вероятность
Тогда
вероятность ![]() равна …
равна …
|
|
|
0,8 |
|
|
|
0,3 |
|
|
|
0,7 |
|
|
|
0,4 |
Решение:
![]()
ЗАДАНИЕ
N 38 сообщить
об ошибке
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина X задана
законом распределения вероятностей:
![]() Тогда
вероятность
Тогда
вероятность ![]() равна …
равна …
|
|
|
0,5 |
|
|
|
0,8 |
|
|
|
0,7 |
|
|
|
0,1 |
Решение:
![]()
ЗАДАНИЕ
N 16 сообщить
об ошибке
Тема:
Законы распределения вероятностей
дискретных случайных величин
Для
дискретной случайной величины X:
 функция
распределения вероятностей имеет
вид:
функция
распределения вероятностей имеет
вид:
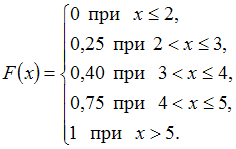 Тогда
значения вероятностей p1, p2, p3 и p5 равны
соответственно …
Тогда
значения вероятностей p1, p2, p3 и p5 равны
соответственно …
|
|
|
0,25; 0,15; 0,35; 0,25 |
|
|
|
0,25; 0,35; 0,15; 0,25 |
|
|
|
0,25; 0,25; 0,25; 0,25 |
|
|
|
0; 0,25; 0,40; 0,75 |
Решение:
По
определению ![]() Следовательно,
Следовательно, ![]()
![]() и
и ![]()
ЗАДАНИЕ
N 21 сообщить
об ошибке
Тема:
Законы распределения вероятностей
дискретных случайных величин
Для
дискретной случайной величины X:
функция
распределения вероятностей имеет
вид:
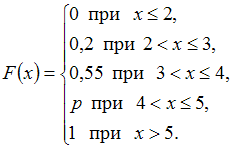 Тогда
значение параметра p может
быть равно …
Тогда
значение параметра p может
быть равно …
|
|
|
0,655 |
|
|
|
1 |
|
|
|
0,25 |
|
|
|
0,45 |
Решение:
По
определению
Следовательно, ![]() и
и ![]() Этим
условиям удовлетворяет, например,
значение
Этим
условиям удовлетворяет, например,
значение ![]()
ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина X задана
законом распределения вероятностей:
 И
вероятность
И
вероятность ![]() Тогда
значения a, b и c могут
быть равны …
Тогда
значения a, b и c могут
быть равны …
|
|
|
a = 0,05, b = 0,30, с = 0,25 |
|
|
|
a = 0,05, b = 0,30 с = 0,35 |
|
|
|
a = 0,05, b = 0,20 с = 0,35 |
|
|
|
a = 0,15, b = 0,30 с = 0,25 |
Решение:
Так
как сумма вероятностей возможных
значений X равна
1, то ![]() А
так как
А
так как ![]() то
то ![]() Следовательно,
Следовательно, ![]() ,
и, например,
,
и, например, ![]()
![]()
ЗАДАНИЕ N 3 сообщить об ошибке Тема: Законы распределения вероятностей дискретных случайных величин Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 36 сообщить об ошибке Тема: Законы распределения вероятностей дискретных случайных величин Среднее число самолетов, прибывающих в аэропорт за 1 мин, равно двум. Тогда вероятность того, что за четыре минуты прибудут ровно шесть самолетов, можно вычислить как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вероятность
наступления k событий
простейшего потока за время t,
определяется формулой Пуассона:
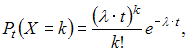 где
где ![]() –
интенсивность потока.
Тогда, так
как
–
интенсивность потока.
Тогда, так
как ![]()
![]()
![]() то
то 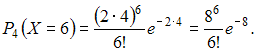
ЗАДАНИЕ N 10 сообщить об ошибке Тема: Законы распределения вероятностей дискретных случайных величин Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
Решение:
Воспользуемся
формулой Бернулли:
![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() Тогда
Тогда ![]()