6.1. Определение вероятности.

  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …

Решение: Для вычисления события A (среди отобранных деталей нет годных) воспользуемся формулой   где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали  из 12 имеющих, то есть   А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три бракованные детали из пяти, то есть   Следовательно, 

  ЗАДАНИЕ N 6 сообщить об ошибке Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …

Решение: Для вычисления события A (среди отобранных деталей нет бракованных) воспользуемся формулой   где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть   А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три небракованные детали из семи, то есть   Следовательно, 

  ЗАДАНИЕ N 20 сообщить об ошибке Тема: Определение вероятности В группе 15 студентов, из которых 6 отличников. По списку наудачу отобраны 5 студентов. Тогда вероятность того, что среди отобранных студентов нет отличников, равна …

Решение: Для вычисления события A (среди отобранных студентов нет отличников) воспользуемся формулой   где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A.  В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно отобрать 5 студентов из 15, то есть   А общее число благоприятствующих исходов равно числу способов, которыми можно отобрать 5 студентов из 9 неотличников, то есть   Следовательно, 

  ЗАДАНИЕ N 1 сообщить об ошибке Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …

			0

Решение: Для вычисления события A (сумма выпавших очков будет равна десяти) воспользуемся формулой  , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны   элементарных исходов испытания, из которых благоприятствующими являются исходы вида  ,   и  ,  то есть m = 3. Следовательно, 

  ЗАДАНИЕ N 12 сообщить об ошибке Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …

			0

Решение: Для вычисления события A (сумма выпавших очков будет равна семи, а разность – трем) воспользуемся формулой   где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны   элементарных исходов испытания, из которых благоприятствующими являются исходы вида   и  ,  то есть m = 2. Следовательно, 

  ЗАДАНИЕ N 15 сообщить об ошибке Тема: Определение вероятности Внутрь круга радиуса 5 наудачу брошена точка. Тогда вероятность того, что точка окажется внутри вписанного в круг равностороннего треугольника, равна …

Решение: Для вычисления вероятности искомого события воспользуемся формулой 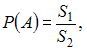  где   – площадь круга, а   – площадь вписанного в круг равностороннего треугольника. Следовательно,  

 ЗАДАНИЕ N 35 сообщить об ошибке Тема: Определение вероятности При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные.  Тогда вероятность того, что номер набран правильно, равна …